Linear Functions Review of Formulas Formula for Slope



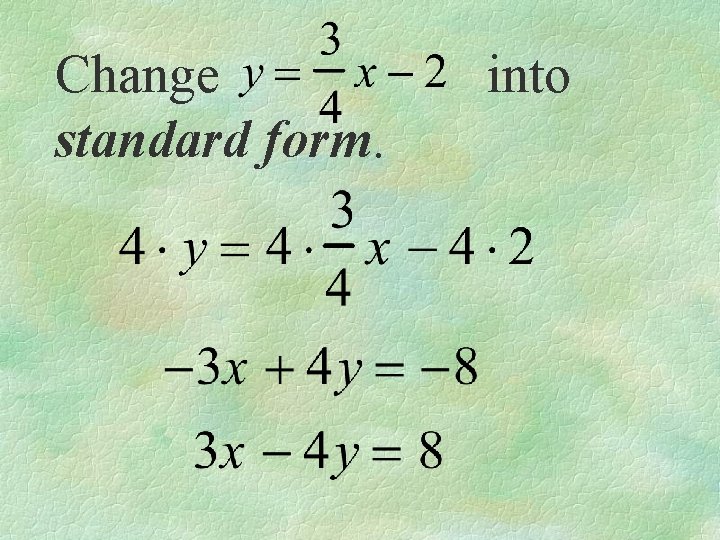












- Slides: 22

Linear Functions

Review of Formulas Formula for Slope Standard Form *where A>0 and A, B, C are integers Slope-intercept Form Point-Slope Form

Find the slope of a line through points (3, 4) and (-1, 6).
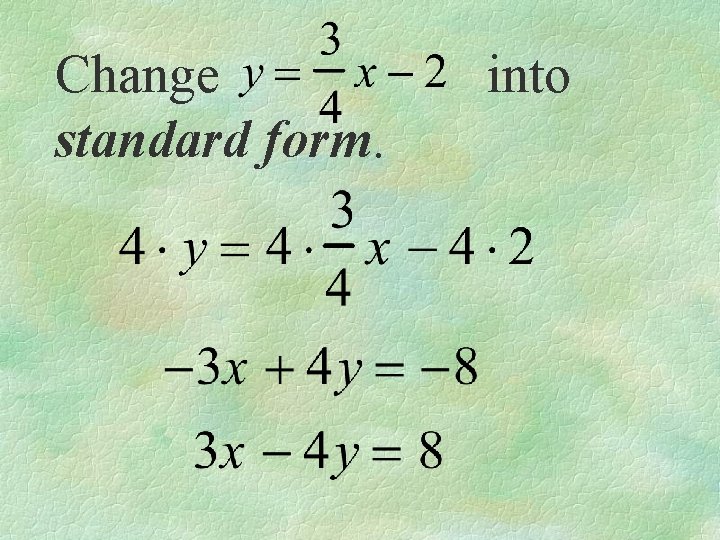
Change standard form. into

Change into slopeintercept form and identify the slope and y-intercept.

Write an equation for the line that passes through (-2, 5) and (1, 7): Find the slope: Use pointslope form:

x-intercepts and y-intercepts The intercept is the point(s) where the graph crosses the axis. To find an intercept, set the other variable equal to zero.

Horizontal Lines § Slope is zero. § Equation form is y = #. Write an equation of a line and graph it with zero slope and y-intercept of -2. y = -2 Write an equation of a line and graph it that passes through (2, 4) and (-3, 4). y=4

Vertical Lines § Slope is undefined. § Equation form is x = #. Write an equation of a line and graph it with undefined slope and passes through (1, 0). x=1 Write an equation of a line that passes through (3, 5) and (3, -2). x=3

Graphing Lines *You need at least 2 points to graph a line. Using x and y intercepts: • Find the x and y intercepts • Plot the points • Draw your line

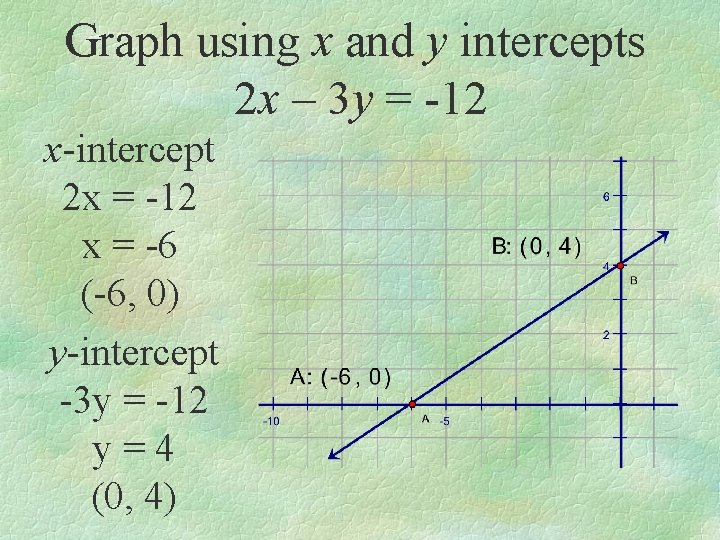
Graph using x and y intercepts 2 x – 3 y = -12 x-intercept 2 x = -12 x = -6 (-6, 0) y-intercept -3 y = -12 y=4 (0, 4)

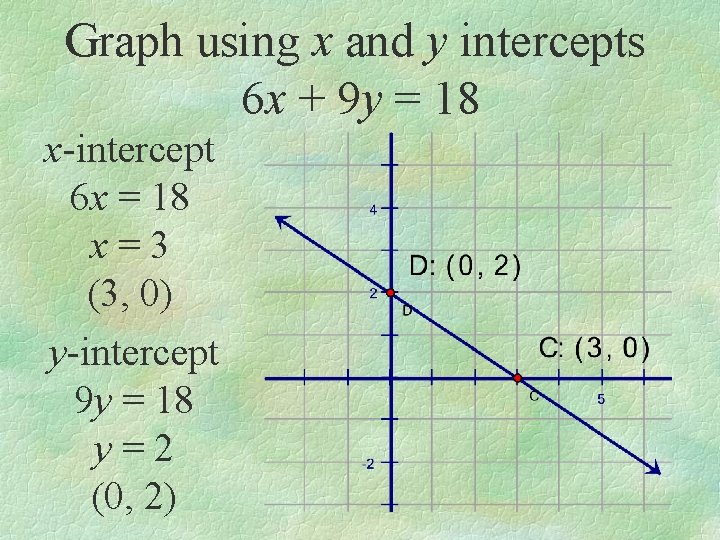
Graph using x and y intercepts 6 x + 9 y = 18 x-intercept 6 x = 18 x=3 (3, 0) y-intercept 9 y = 18 y=2 (0, 2)

Graphing Lines Using slope-intercept form y = mx + b: • Change the equation to y = mx + b. • Plot the y-intercept. • Use the numerator of the slope to count the corresponding number of spaces up/down. • Use the denominator of the slope to count the corresponding number of spaces left/right. • Draw your line.

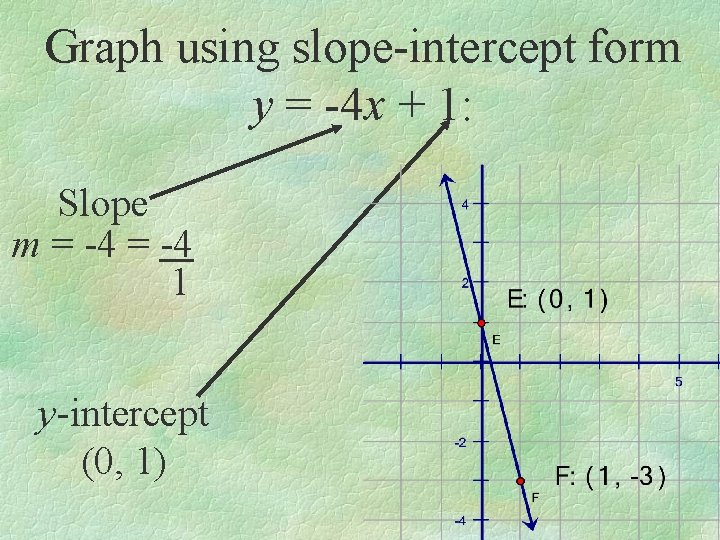
Graph using slope-intercept form y = -4 x + 1: Slope m = -4 1 y-intercept (0, 1)

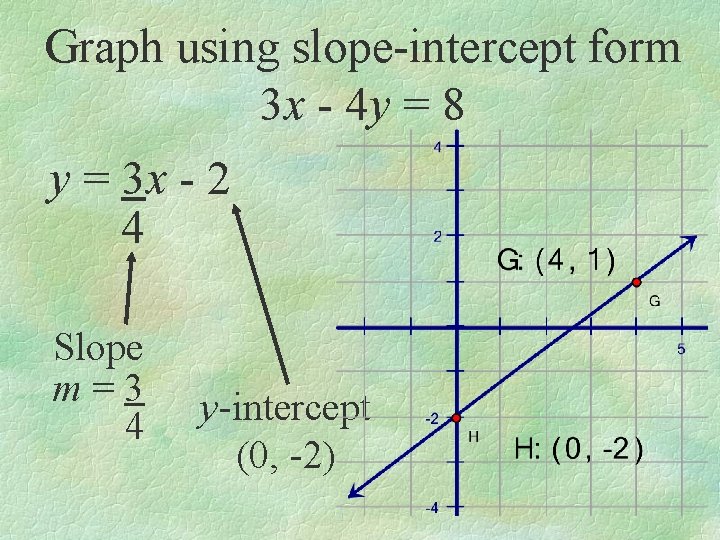
Graph using slope-intercept form 3 x - 4 y = 8 y = 3 x - 2 4 Slope m=3 4 y-intercept (0, -2)

Parallel Lines **Parallel lines have the same slopes. • Find the slope of the original line. • Use that slope to graph your new line and to write the equation of your new line.

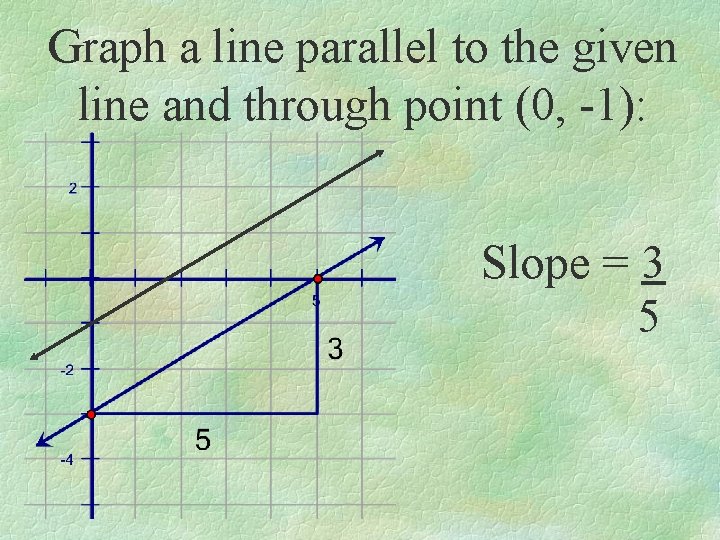
Graph a line parallel to the given line and through point (0, -1): Slope = 3 5

Write the equation of a line parallel to 2 x – 4 y = 8 and containing (-1, 4): – 4 y = - 2 x + 8 y = 1 x - 2 2 Slope = 1 2 y - 4 = 1(x + 1) 2

Perpendicular Lines **Perpendicular lines have the opposite reciprocal slopes. • Find the slope of the original line. • Change the sign and invert the numerator and denominator of the slope. • Use that slope to graph your new line and to write the equation of your new line.

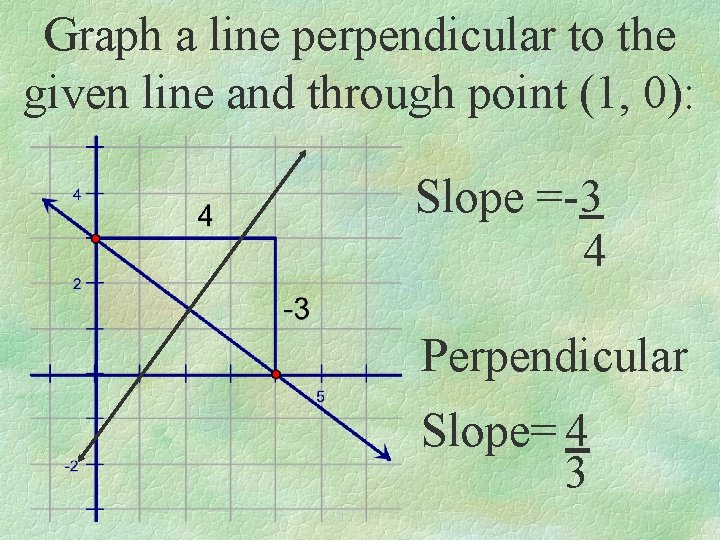
Graph a line perpendicular to the given line and through point (1, 0): Slope =-3 4 Perpendicular Slope= 4 3

Write the equation of a line perpendicular to y = -2 x + 3 and containing (3, 7): Original Slope= -2 Perpendicular Slope = 1 2 y - 7 = 1(x - 3) 2

Write the equation of a line perpendicular to 3 x – 4 y = 8 and containing (-1, 4): -4 y = -3 x + 8 Slope= 3 4 Perpendicular Slope = -4 3 y - 4 = -4(x + 1) 3