Linear Functions Math I Day 1 Introduction to

Linear Functions Math I

Day 1 Introduction to Linear Functions & Slope intercept form

Learn to identify linear functions.

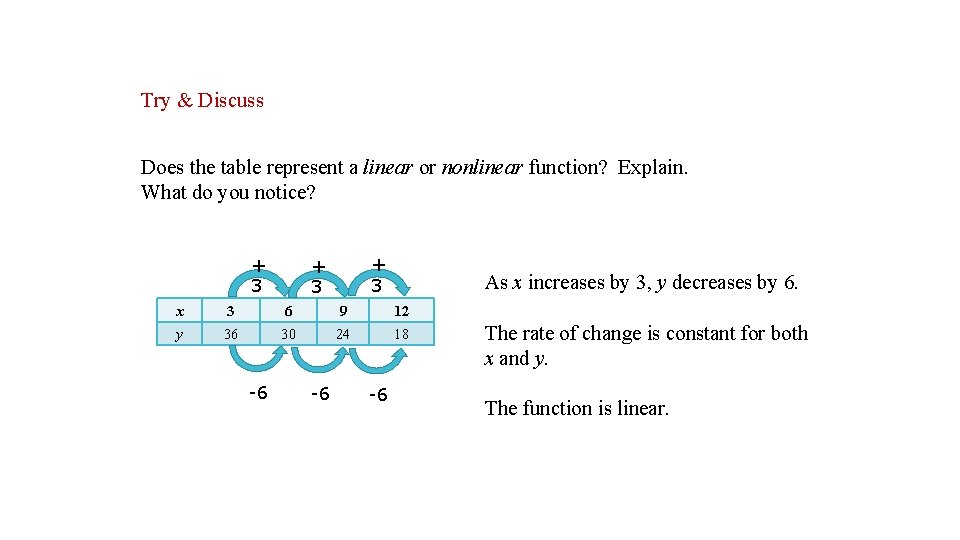
Try & Discuss Does the table represent a linear or nonlinear function? Explain. What do you notice? + 3 + 3 As x increases by 3, y decreases by 6. x 3 6 9 12 y 36 30 24 18 -6 -6 -6 The rate of change is constant for both x and y. The function is linear.

Connect: About Linear Functions

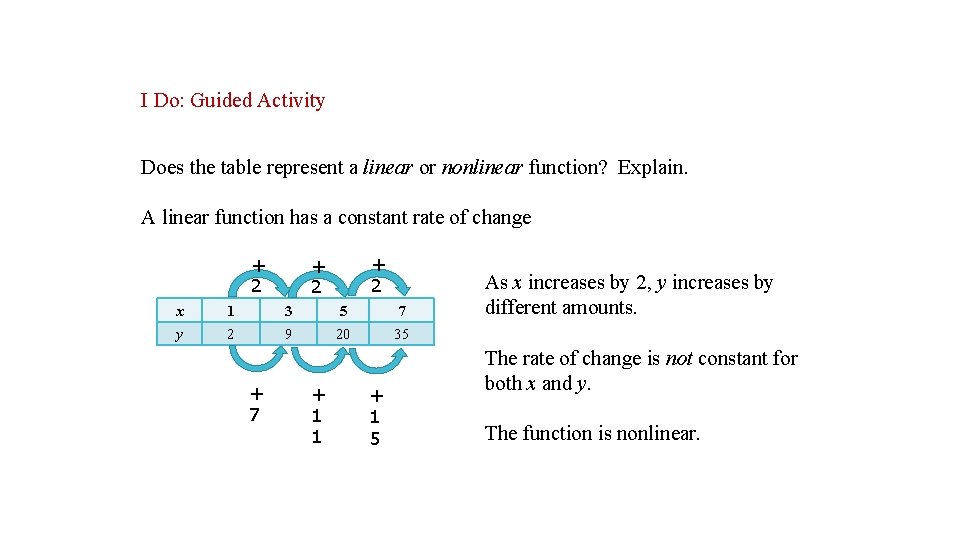
I Do: Guided Activity Does the table represent a linear or nonlinear function? Explain. A linear function has a constant rate of change + 2 + 2 x 1 3 5 7 y 2 9 20 35 + 7 + 1 1 + 1 5 As x increases by 2, y increases by different amounts. The rate of change is not constant for both x and y. The function is nonlinear.

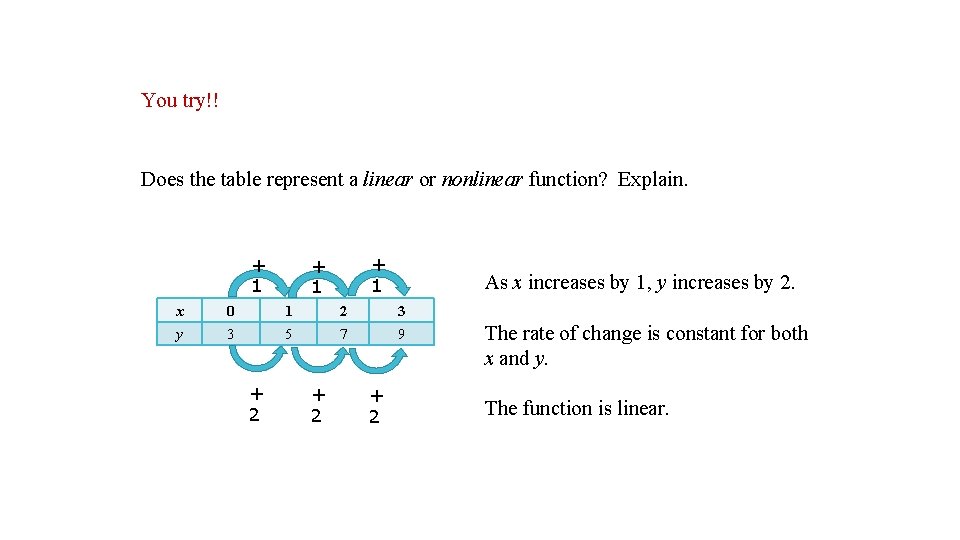
You try!! Does the table represent a linear or nonlinear function? Explain. + 1 + 1 As x increases by 1, y increases by 2. x 0 1 2 3 y 3 5 7 9 + 2 + 2 The rate of change is constant for both x and y. The function is linear.

Try Additional Example 1: Identifying Linear Functions TRY: Determine whether the function f(x) = -2 x + 4 is linear. What Information would we need to graph this equation? How can we determine this information from the equation? Would this equation represent a linear function?

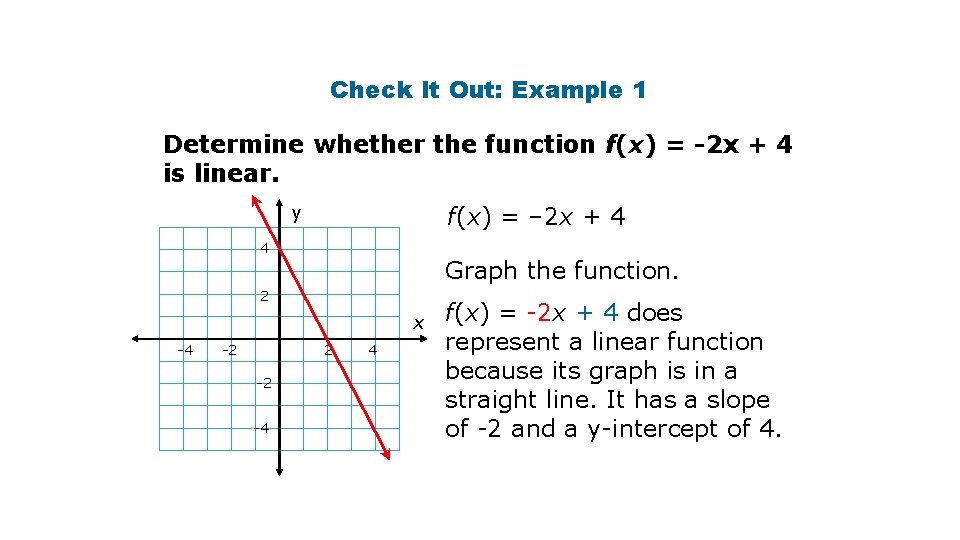
Check It Out: Example 1 Determine whether the function f(x) = -2 x + 4 is linear. f(x) = – 2 x + 4 y 4 Graph the function. 2 x -4 -2 2 -2 -4 4 f(x) = -2 x + 4 does represent a linear function because its graph is in a straight line. It has a slope of -2 and a y-intercept of 4.

Notes: Graphing Lines Using slope-intercept form y = mx + b: • Plot the y-intercept. • Use the numerator of the slope to count the corresponding number of spaces up/down. • Use the denominator of the slope to count the corresponding number of spaces left/right. • Draw your line.

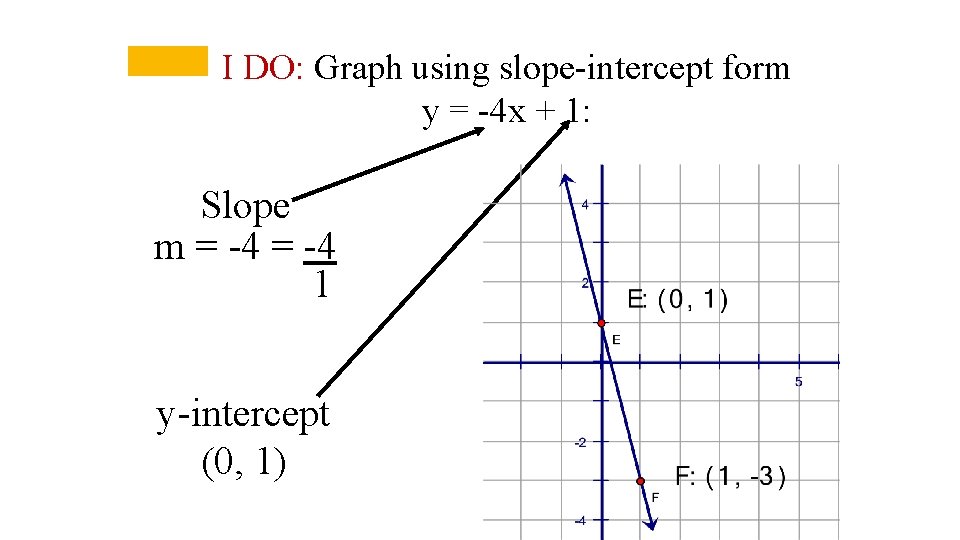
I DO: Graph using slope-intercept form y = -4 x + 1: Slope m = -4 1 y-intercept (0, 1)

You Try y = 3 x - 2 4 Slope m=3 4 y-intercept (0, -2)

So let’s review! What have we covered so far?

Independent or Group Independent Practice: Desmos activity “Turtle Time Trials” Group A Today! Review test problems (CFA 2)

Day 2: Writing Linear Functions/Rules

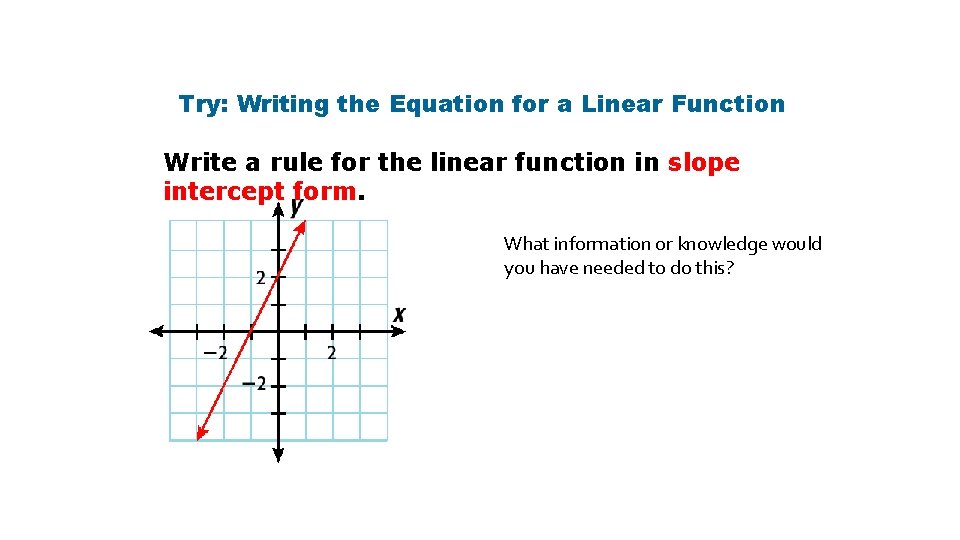
Try: Writing the Equation for a Linear Function Write a rule for the linear function in slope intercept form. What information or knowledge would you have needed to do this?

Try: Writing the Equation for a Linear Function Write a rule for the linear function (slope intercept form). Step 1 Identify the y-intercept b from the graph. b=2 Step 2 Locate another point on the graph, such as (1, 4). Step 3 Substitute the x- and y-values of the point into the equation, f(x) = mx + b, and solve for m.

Additional Example 2 A Continued f(x) = mx + b 4 = m(1) + 2 4=m+2 – 2 2=m The rule is f(x) = 2 x + 2. (x, y) = (1, 4)

We Try: Writing the Equation for a Linear Function Write a rule for the linear function. x y – 3 – 8 – 1 – 2 1 4 3 10 What information would you need to know? How can you manipulate the table to give you that information?

We Try: Writing the Equation for a Linear Function Write a rule for the linear function (formula for slope). Step 1 Locate two points. x y – 3 – 8 (1, 4) and (3, 10) – 1 – 2 Step 2 Find the slope m. 1 4 3 10 y 2 – y 1 10 – 4 6 m = x 2 – x 1 = 3 – 1 = = 3 2 Step 3 Substitute the x- and y-values of the point into the equation, f(x) = mx + b, and solve for b.

Additional Example 2 B Continued f(x) = mx + b 4 = 3(1) + b 4= 3+b – 3 1= b The rule is f(x) = 3 x + 1. (x, y) = (1, 4)

You do: Example 1 Write a rule for the linear function. Step 1 Identify the y-intercept b from the graph. y 4 b=1 2 x -4 -2 2 -4 4 Step 2 Locate another point on the graph, such as (5, 2). Step 3 Substitute the x- and y-values of the point into the equation, f(x) = mx + b, and solve for m.

Check It Out: Example 2 A Continued f(x) 2 2 – 1 1 = mx + b = m(5) + 1 = 5 m + 1 – 1 = 5 m m=1 5 1 x + 1. The rule is f(x) = 5 (x, y) = (5, 2)

You do: Example 2 Write a rule for the linear function. x y Step 1 Locate two points. 0 5 (0, 5) and (1, 6) 1 6 2 7 – 1 4 Step 2 Find the slope m. y 2 – y 1 6 – 5 m = x 2 – x 1 = 1 – 0 = 1 1 Step 3 Substitute the x- and y-values of the point into the equation, f(x) = mx + b, and solve for b.

Check It Out: Example 2 B Continued f(x) = mx + b 5 = 1(0) + b 5= b (x, y) = (0, 5) The rule is f(x) = x + 5.

I do: Money Application A video club cost $15 to join. Each video that is rented costs $1. 50. Find a rule for the linear function that describes the total cost of renting videos as a member of the club, and find the total cost of renting 12 videos. f(x) = mx + 15 The y-intercept is the cost to join, $15. 16. 5 = m(1) + 15 With 1 rental the cost will be $16. 50. 16. 5 = m + 15 The rule for the function is f(x) = – 15 1. 5 x + 15. After 12 video rentals, the 1. 5 = m cost will be f(12) = 1. 5(12) + 15 = 18 + 15 = $33.

You try: Example A book club has a membership fee of $20. Each book purchased costs $2. Find a rule for the linear function that describes the total cost of buying books as a member of the club, and find the total cost of buying 10 books. f(x) = mx + 20 The y-intercept is the cost to join, $20. With 1 book purchase the cost will be 22 = m(1) + 20 $22. 22 = m + 20 The rule for the function is – 20 f(x) = 2 x + 20. After 10 books 2=m purchases, the cost will be f(10) = 2(10) + 20 = 20 + 20 = $40.

Independent or Group Independent: Desmos activity “Match my Line” Group B and C Today!

Day 3 From Standard Form to Slope Intercept form Converting to slope intercept from standard form Graphing from standard form

Try: Convert the equation from standard form to slopeintercept form: Example 1 2 x + 3 y = 12 What is it that you need to make this work Hint: formulas, etc

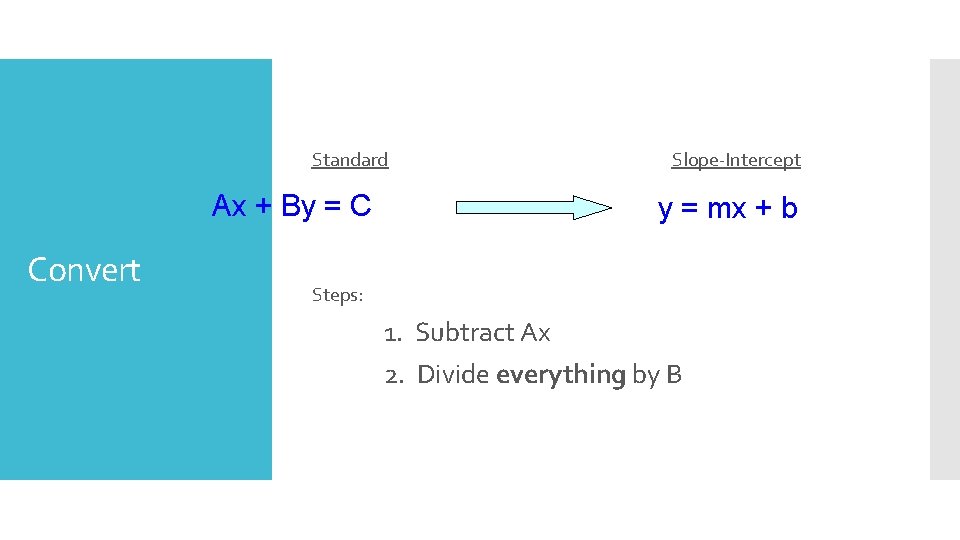
Standard Ax + By = C Convert Slope-Intercept y = mx + b Steps: 1. Subtract Ax 2. Divide everything by B

You do: Example 2 Convert the equation from standard form to slopeintercept form: 2 x – y = -4

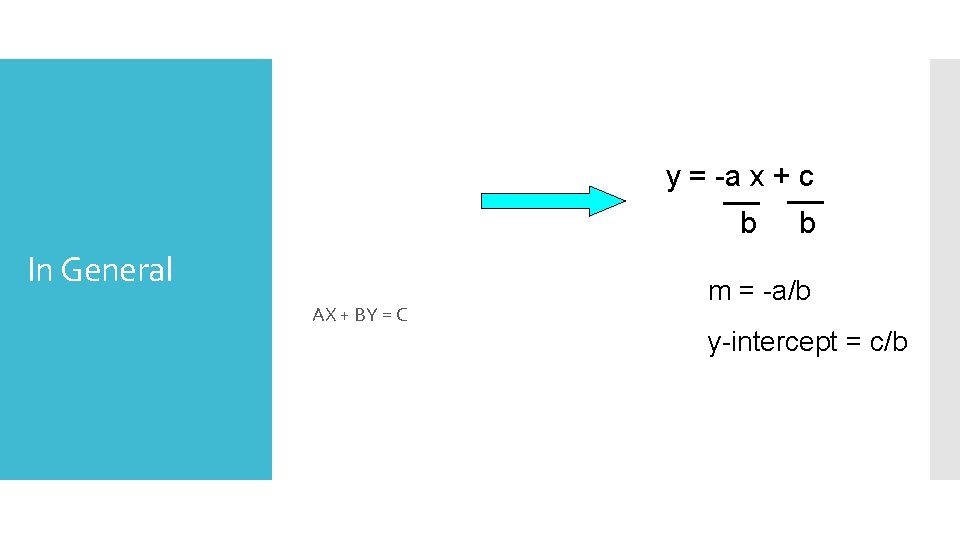
y = -a x + c b In General AX + BY = C b m = -a/b y-intercept = c/b

Write your equation in STANDARD form given m = and b = 2. First, write in slope-intercept form: y= x+2 Now, write it in standard form. (Ax + By = C where A, B, and C are integers). Clear the fractions - multiply everything by 3. (3)y = (3)( x) + (3)2 3 y = -x + 6 Get the variables on the same side. x + 3 y = 6

Write the standard form for a line passing through the points (-1, -3) and (-4, 6). Oh no! This is a Type #3 problem! Find slope… Find y-intercept. I’m choosing the point (-4, 6). 6 = -3(-4) + b 6 = 12 + b -6 = b Slope-intercept form: y = -3 x - 6 Standard form: 3 x + y = -6

Independent Complete the Desmos activity : “Put the Point on the Line”

Graphing Standard Form Day 4 Parallel and Perpendicular Lines

Graphing Lines *You need at least 2 points to graph a line. Using x and y intercepts: • Find the x and y intercepts • Plot the points • Draw your line

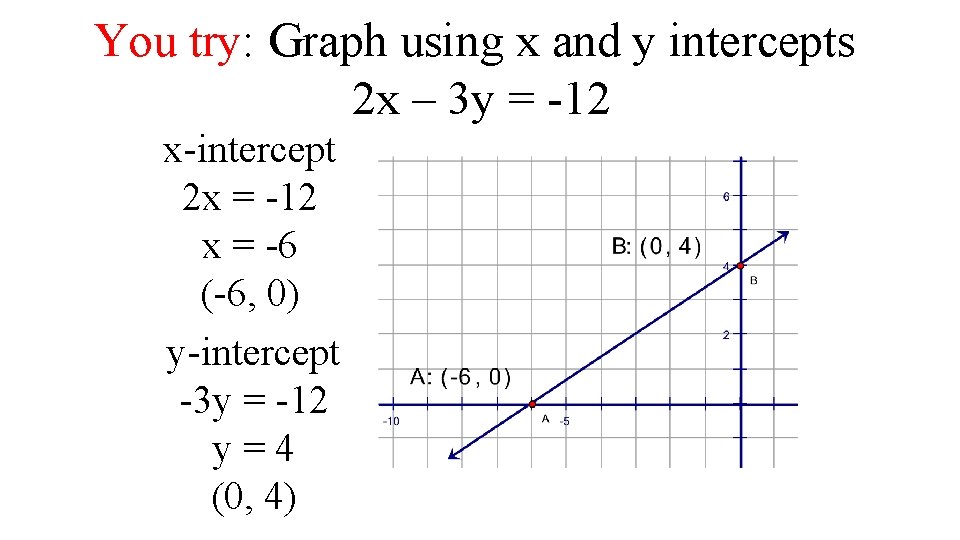
You try: Graph using x and y intercepts 2 x – 3 y = -12 x-intercept 2 x = -12 x = -6 (-6, 0) y-intercept -3 y = -12 y=4 (0, 4)

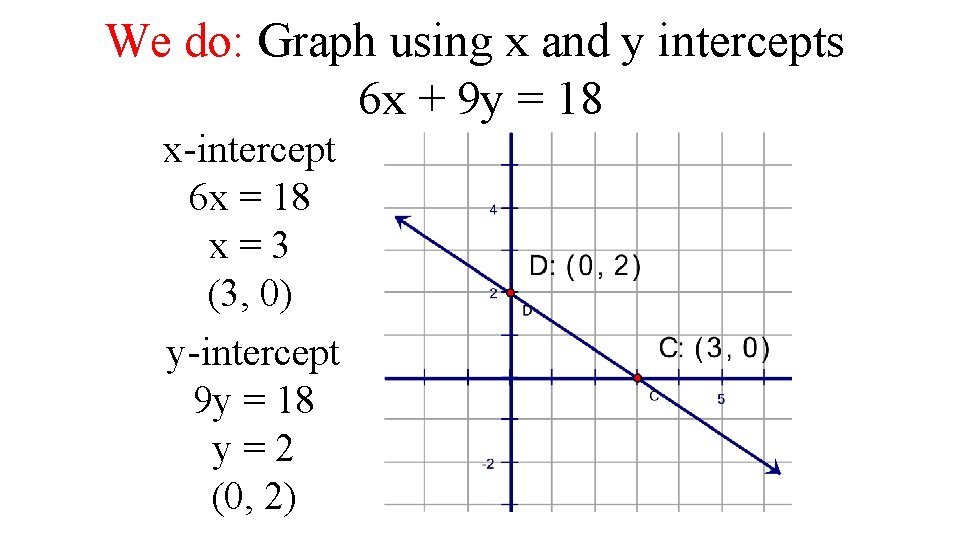
We do: Graph using x and y intercepts 6 x + 9 y = 18 x-intercept 6 x = 18 x=3 (3, 0) y-intercept 9 y = 18 y=2 (0, 2)

NOTES: Parallel Lines **Parallel lines have the same slopes. • Find the slope of the original line. • Use that slope to graph your new line and to write the equation of your new line.

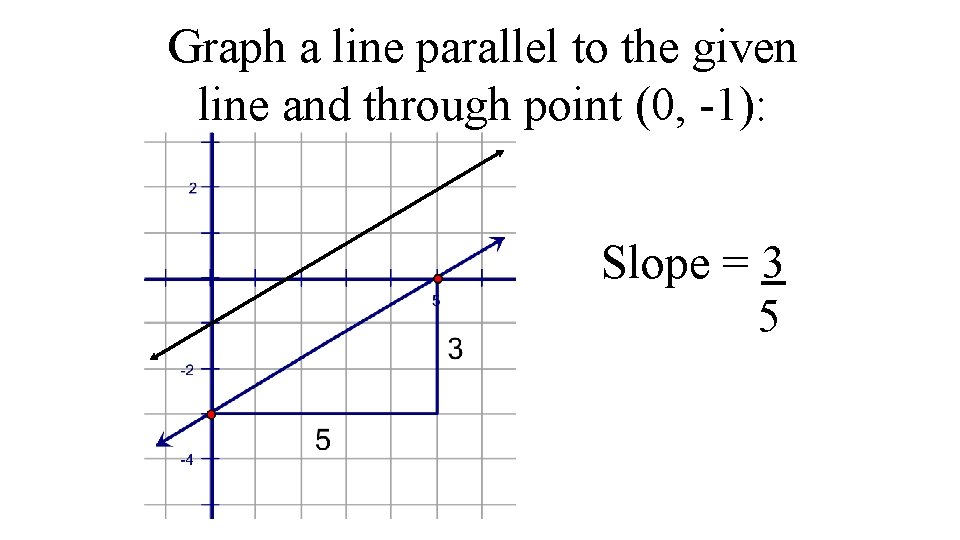
Graph a line parallel to the given line and through point (0, -1): Slope = 3 5

Write the equation of a line parallel to 2 x – 4 y = 8 and containing (-1, 4): – 4 y = - 2 x + 8 y = 1 x - 2 2 Slope = 1 2 y - 4 = 1(x + 1) 2

Perpendicular Lines **Perpendicular lines have the opposite reciprocal slopes. • Find the slope of the original line. • Change the sign and invert the numerator and denominator of the slope. • Use that slope to graph your new line and to write the equation of your new line.

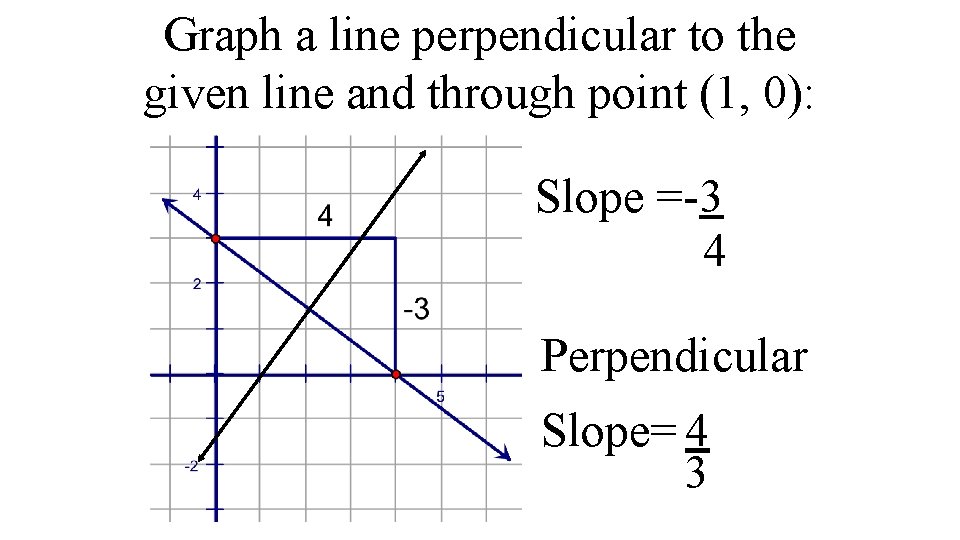
Graph a line perpendicular to the given line and through point (1, 0): Slope =-3 4 Perpendicular Slope= 4 3

Write the equation of a line perpendicular to y = -2 x + 3 and containing (3, 7): Original Slope= -2 Perpendicular Slope = 1 2 y - 7 = 1(x - 3) 2

Write the equation of a line perpendicular to 3 x – 4 y = 8 and containing (-1, 4): -4 y = -3 x + 8 Slope= 3 4 Perpendicular Slope = -4 3 y - 4 = -4(x + 1) 3

Independent or group Independent: Complete the desmos activity “Parallel Lines” Group A today!

Day 5 Quick Review/ Revision- Linear Functions

Lesson Quiz: Part I Determine whether each function is linear. 1. f(x) = 4 x 2 not linear 2. f(x) = 3 x + 1 linear Write the rule for the linear function. f(x) = 1 x - 1 2

Lesson Quiz: Part II Write the rule for each linear function. 2. x y – 3 0 3 – 10 – 1 8 5 7 14 20 f(x) = 3 x – 1 3. Andre sells toys at the craft fair. He pays $60 to rent the booth. Materials for his toys are $4. 50 per toy. Find a rule for the linear function that describes Andre's expenses for the day. Determine his expenses if he sold 25 toys. f(x) = 4. 50 x + 60; $172. 50

Independent or Group Independent activity on Desmos: “Card Sort: Linear Functions” Group Activity: Group B today!