Linear Functions Identify and Graph Linear Equations Name

Linear Functions Identify and Graph Linear Equations Name and Graph X and Y Intercepts

Vocabulary for this lesson Linear Equation – the equation of a line whose graph is a straight line. n Standard Form – Linear equations written in the form Ax + By = C n X-Intercept – the point where a graphed line crosses the x-axis. n Y-Intercept – the point where a graphed line crosses the y-axis. n

Determine whether each equation is linear…. if so, write it in Standard Form 1) y = 5 – 2 x +2 x 2 x + y = 5 n Can it be written in standard form? Ax + By = C 2) y = -3 – x +x +x x + y = -3 3) 2 xy – 5 y = 6 Why? . . The first term has TWO variables.

(3) n Can it be written in standard form? Ax + By = C (3) 4) 1/3 y = -1 y = -3 5) 5 x + 3 y = z + 2 Why? . . It has an extra variable “z”. 6) y = x 2 – 8 Why? . . Because the “x” is squared. To be considered LINEAR, an equation must have a degree of ONE.

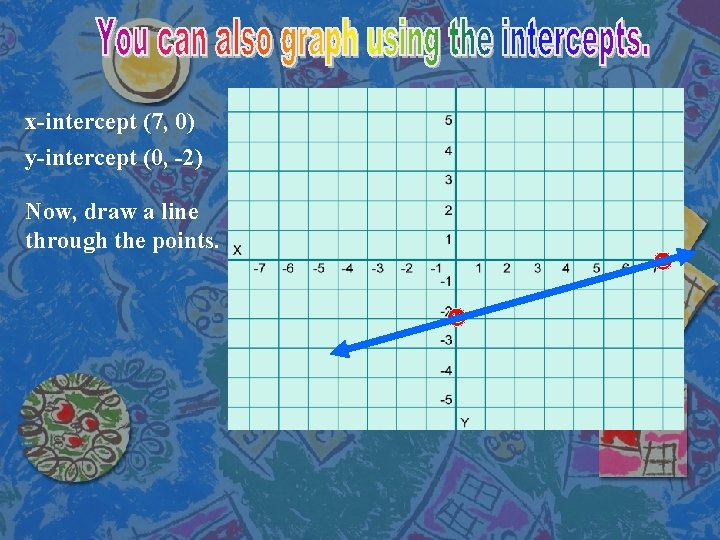
x and y - Intercepts To find the x-intercept, let y=0 The x-int. is 7, so the graph intersects the x -axis at (7, 0) To find the y-intercept, let x=0 The y-int. is -2, so the graph intersects the y -axis at (0, -2)

x-intercept (7, 0) y-intercept (0, -2) Now, draw a line through the points.

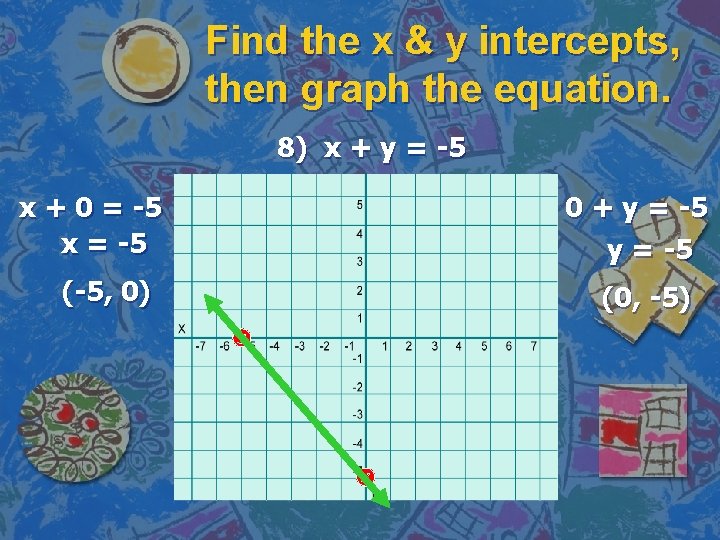
Find the x & y intercepts, then graph the equation. 8) x + y = -5 x + 0 = -5 x = -5 (-5, 0) 0 + y = -5 (0, -5)

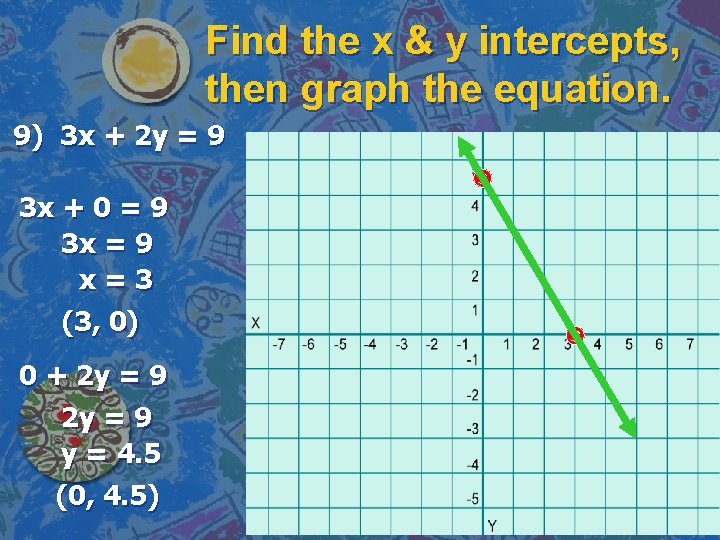
Find the x & y intercepts, then graph the equation. 9) 3 x + 2 y = 9 3 x + 0 = 9 3 x = 9 x=3 (3, 0) 0 + 2 y = 9 y = 4. 5 (0, 4. 5)

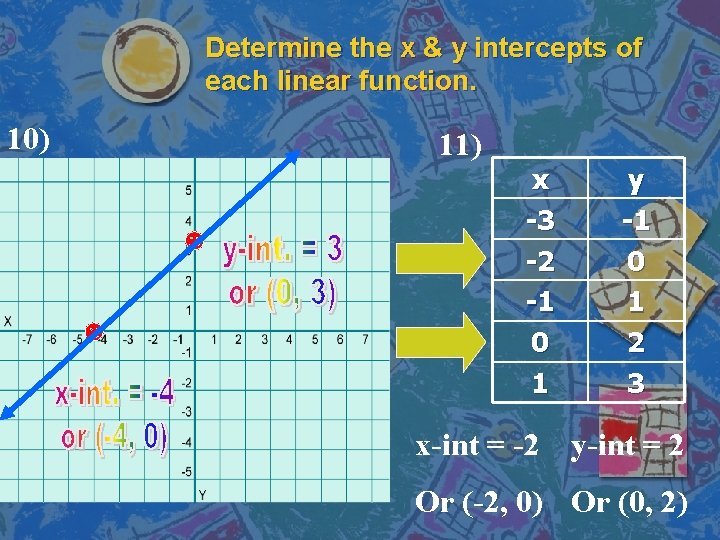
Determine the x & y intercepts of each linear function. 10) 11) x -3 -2 -1 0 1 y -1 0 1 2 3 x-int = -2 y-int = 2 Or (-2, 0) Or (0, 2)

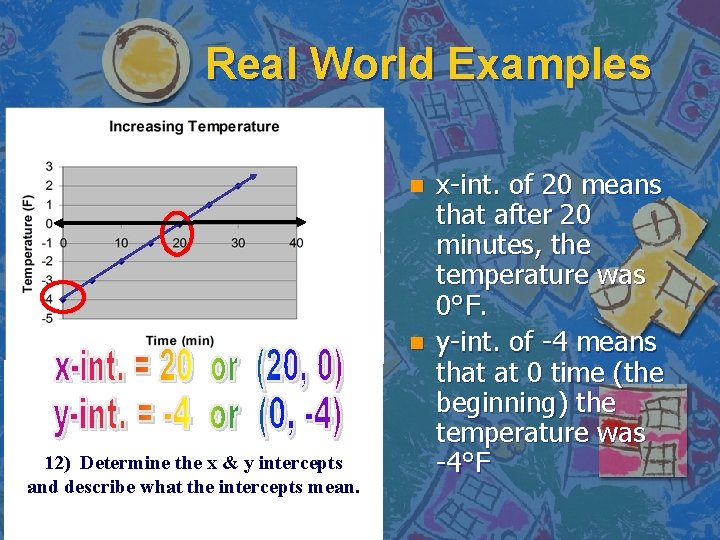
Real World Examples n n 12) Determine the x & y intercepts and describe what the intercepts mean. x-int. of 20 means that after 20 minutes, the temperature was 0°F. y-int. of -4 means that at 0 time (the beginning) the temperature was -4°F

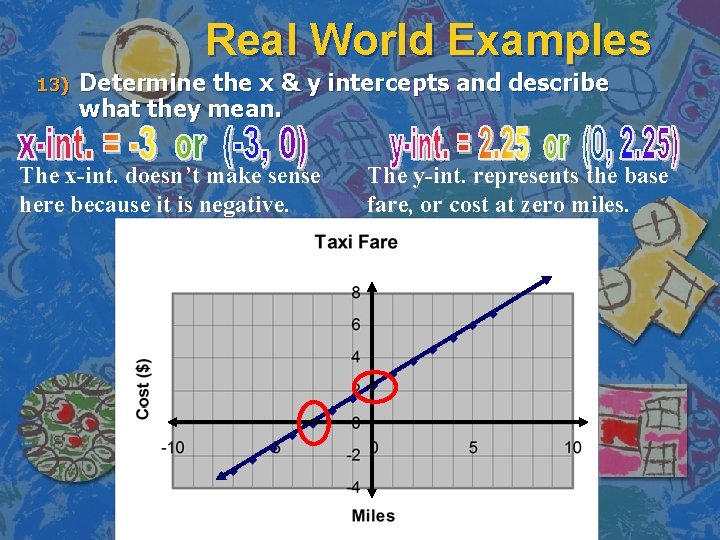
Real World Examples 13) Determine the x & y intercepts and describe what they mean. The x-int. doesn’t make sense here because it is negative. The y-int. represents the base fare, or cost at zero miles.

Determine the Intercepts and explain each. 14) Draining a pool Time (h) Volume (g) 0 2 4 10, 080 8640 7200 15) Position of a The x-int. shows scuba diver. that after 12 sec. , Time (s) Depth (m) 0 3 6 9 12 -24 -18 -12 -6 0 the diver was at the surface (0 m). The y-int. shows that when he started (0 s) he was at -24 m or 24 m below sea level. 6 5760 8 4320 10 2880 14 0 The x-int. shows that after 14 hours, the pool had 0 gallons, or it was completely drained. The y-int. shows that at 0 hours, when they began, it had 10, 080 gallons in it.