Linear Equations Overview of LUP Decomposition Using floating

Linear Equations

Overview of LUP Decomposition • Using floating point numbers on a computer, finding a matrix inverse is numerically unstable Multiply Ax = b by P to get PAx = Pb, use 31. 20 to get LUx = Pb Let y = Ux, then Ly = Pb is solved by forward substitution Solve Ux=y for x by back substitution, this is the solution for Ax=b

Forward Substitution • We have the solution for y 1 from the first equation; substitute in the second equation to find y 2; continue on in this manner; in general

Backward Substitution

Example - 1

Example - 2

Computing an LU Decomposition • We first consider the case where the permutation matrix is the identity matrix • We use Gaussian Elimination – subtract multiples of the first equation from the remaining equations to remove the first variable – subtract multiples of the second equation from the remaining equations to remove the second variable – continue in this manner until the remaining coefficients are in upper triangular form • For n = 1 we are done; for larger n we will use a recursive strategy

Finding L and U • We first decompose A into the Schur complement • We recursively find the LU decomposition of the Schur complement

Pivoting and the LU Algorithm • Pivoting –since we divide by a 11, it cannot be zero, it is called a pivot –the same is true at the next recursive step –the permutation matrix P is used to insure that all pivots are not zero; if the matrix is positive-definite we do not need P –Notice an iterative loop replaces recursion –the code only computes the “significant” entries (not the 0’s or 1’s) –the complexity is (n 3)

Example Computation

The LUP Decomposition - 1 • We first multiply by Q, a matrix that interchanges row k with row 1 assuring that the pivot is nonzero • We inductively find the LUP decomposition for the Schur complement • Let P be • On the next slide we show that PA leads to the desired decomposition

The LUP Decomposition - 2

LUP Decomposition Algorithm • The permutation matrix has (i) = j meaning the ith row has a 1 in the jth column • L and U are computed in place in the matrix A; when the algorithm terminates • the complexity is (n 3)

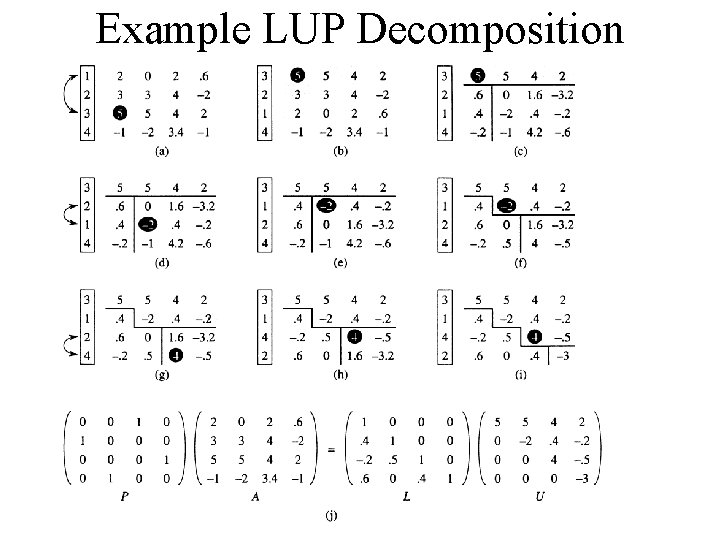
Example LUP Decomposition

Matrix Inversion • Using LUP decomposition to solve Ax = In you can find a matrix inverse in (n 3) time