LINEAR EQUATION IN TWO VARIABLES Determinant method of

LINEAR EQUATION IN TWO VARIABLES .

*Determinant method of solving simultaneous equation

We have studied the graphical method for solving simultaneous equations. It has certain limitations. We can overcome these limitations by using the determinant method of solving simultaneous equations. Let us first see what is meant by a determinant.

If a , b , c & d are any four numbers , the value ad – bc is represented as ab cd This type of representation of number is called as determinant of order two as it has two rows & two columns. the value of the determinant a b c d is ab- bc.

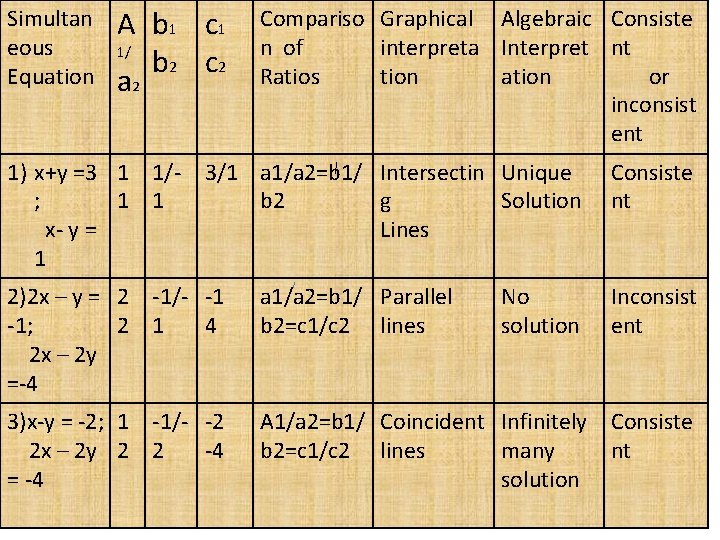
Simultan eous Equation A b 1 c 1 1/ b 2 c 2 a 2 Compariso Graphical Algebraic Consiste n of interpreta Interpret nt Ratios tion ation or inconsist ent 1) x+y =3 1 1/- 3/1 a 1/a 2=b 1/ Intersectin Unique ; 1 1 b 2 g Solution x- y = Lines 1 Consiste nt 2)2 x – y = 2 -1/- -1 -1; 2 1 4 2 x – 2 y =-4 a 1/a 2=b 1/ Parallel b 2=c 1/c 2 lines Inconsist ent 3)x-y = -2; 1 -1/- -2 2 x – 2 y 2 2 -4 = -4 A 1/a 2=b 1/ Coincident Infinitely Consiste b 2=c 1/c 2 lines many nt solution No solution

1] X+3 y+4 = 0 ; 2 x+6 y-3= 0 x+3 y+4=0 and 2 x+6 y-3=0 can be written as x+3 y=-4 and 2 x+6 y=3 respectively. Comparing the above equation with the equation a 1 x + b 1 y =c 1 and ax 2+b 2 y=c 2, we get ,

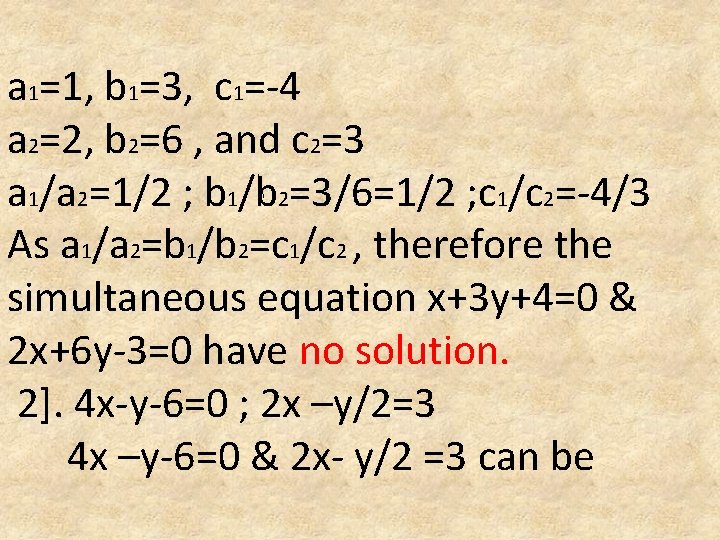
a 1=1, b 1=3, c 1=-4 a 2=2, b 2=6 , and c 2=3 a 1/a 2=1/2 ; b 1/b 2=3/6=1/2 ; c 1/c 2=-4/3 As a 1/a 2=b 1/b 2=c 1/c 2 , therefore the simultaneous equation x+3 y+4=0 & 2 x+6 y-3=0 have no solution. 2]. 4 x-y-6=0 ; 2 x –y/2=3 4 x –y-6=0 & 2 x- y/2 =3 can be

2]. 4 x-y-6 = 0 ; 2 x-y/2=3 4 x-y-6 = 0 & 2 x-y/2=3 can be written as 4 x-y=6 & 2 x -1/2 y =3 respectively. Comparing the above equation with the equation a 1 x+b 1 y=c 1 & a 2 x+b 2 y=c 2, we get, 1= a 1=4 , b 1=-1 c 1=6 a 2=2 , b 2=-1/2 & c 2=3 a 1/a 2=4/2=2/1; b 1/b 2=-1/-1/2=2/1 & c 1/c 2 =6/3=2/1 As a 1/a 2=b 1/b 2=c 1/c 2 , therefore the simultaneous equations 4 x-y-6=0 & 2 x-y/2=3 have infinitely many solution.

3]. Y=2 x=14; 7 x=2 y=5 Y=2 x=14 & 7 x=2 y=5 can be written as 2 x-y=-14 & 7 x-2 y=5 respectively. Comparing the above equations with the equations a 1 x+b 1 y=c 1 & a 2 x+b 2 y=c 2, we get, a 1=2 , b 1=-1 , c 1=-14 , a 2=7, b 2=-2 , & c 2=5 a 1/a 2=2/7 ; b 1/b 2 =-1/-2=1/2 & c 1/c 2 =-14/5 As a 1/a 2 b 1/b 2, therefore the simultaneous equation y=2 x + 14 & 7 x=2 y+5 have unique soltion.

Equation reducible to a pair of liner equation in two variable. SOLVED EXAMPLES

Solve the following simultaneous equations : 1] 4/x + 3/y=1 ; 8/x-9/y =7 solution: 4/x + 3/y=1 ………(1) 8/x-9/y =7 …………(2) substituing 1/x=m & 1/y=n in the above, equation we get 4 m+ 3 n =1 ………(3) & 8 m-9 n=7 …………(4) multiplying equation (3) by 2 we get , 8 m-9 n=7 8 m+6 n=2 - - -15 n=5

n=-1/3 substituing n=-1/3 in equation (3) we get , m=1/2 Resubstituting the values of m & n we get , 1/x=1/2 & 1/y=-1/3 x=2 & y=-3.

solved examples

1] The entry ticket for an exhibition is Rs. 5 for children & Rs. 15 for adults. A group of thirteen persons visited this exhibition & paid Rs. 115 to buy entry tickets. Find the number of children & adults in the said group. soltion: let the number of children & adults be x & y respectively. Therefore, the amount required for entry tickets of children & adults will be Rs. 5 x & Rs. 15 y respectively. from the first condition , we get 5 x + 15 y = 115 …………(1)

From the secondition, we get x+y =13 …………(2) mutiply equation (2) by 5, 5 x+15 y = 65 ………. . . (3) Subtract equation (3) from equation (1) 5 x + 15 y = 115 5 x + 5 y =65 - 10 y=50 y=5

Substituting the value of y in equation (2) , x + y = 13 x=8 The number of children is 8 & number of adults is 5.

THANK YOU

THE END