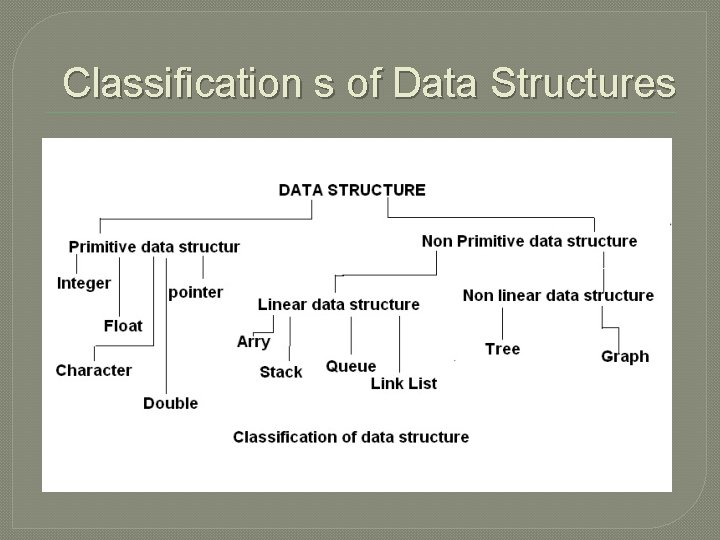
Linear Data Structures using Sequential organization Classification s

Linear Data Structures using Sequential organization

Classification s of Data Structures

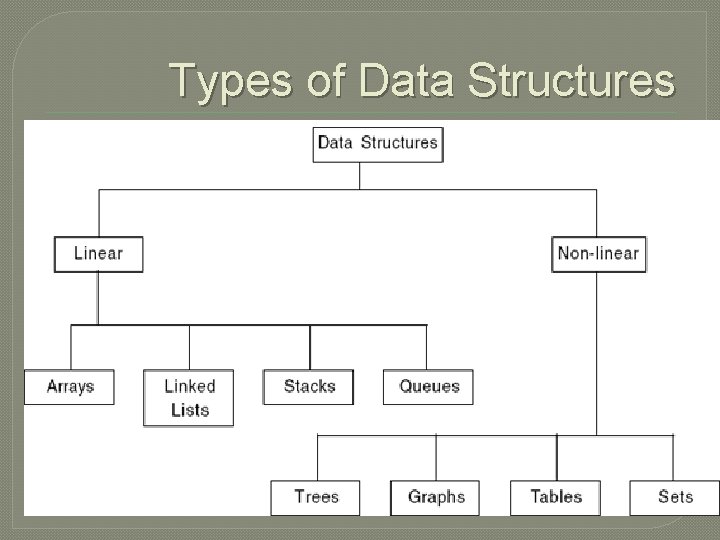
Types of Data Structures

Arrays �Declaration of arrays type array. Name [ array. Size ]; Ex-double balance[10];

Arrays � Initializing Arrays Ex-double balance[5] = {1000. 0, 2. 0, 3. 4, 7. 0, 50. 0}; If you omit the size of the array, an array just big enough to hold the initialization is created. Therefore, if you write − Ex-double balance[] = {1000. 0, 2. 0, 3. 4, 7. 0, 50. 0};

Arrays � Initializing Arrays Ex-double balance[5] = {1000. 0, 2. 0, 3. 4, 7. 0, 50. 0}; If you omit the size of the array, an array just big enough to hold the initialization is created. Therefore, if you write − Ex-double balance[] = {1000. 0, 2. 0, 3. 4, 7. 0, 50. 0};

Arrays �Initializing Arrays �You will create exactly the same array as you did in the previous example. Following is an example to assign a single element of the array − Ex-balance[4] = 50. 0;

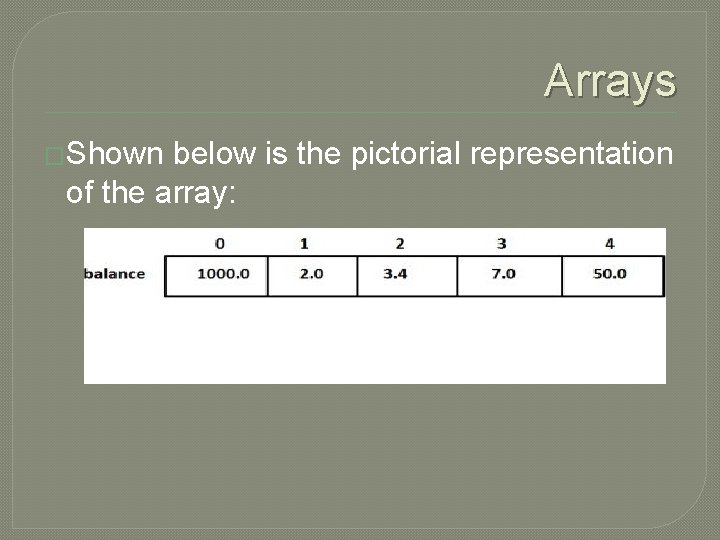
Arrays �Shown below is the pictorial representation of the array:

Accessing Array Elements �double salary = balance[4];

#include <stdio. h> int main () { int a[10], i, size; Ex-Arrays printf(“nhow many no of elements u want to scan”); scanf(“%d”, &size); printf(“n. Enter the elements in the array”); for(i=0; i<size; i++) { scanf(“%d”, &a[i]); } //end for(i=0; i<size; i++) { printf(“The array is %d”, a[i]); //Displaying Array } //end for return 0; }

Output will be 1 2 3 4 5

Multi-dimensional Arrays in C �type name[size 1][size 2]. . . [size. N];

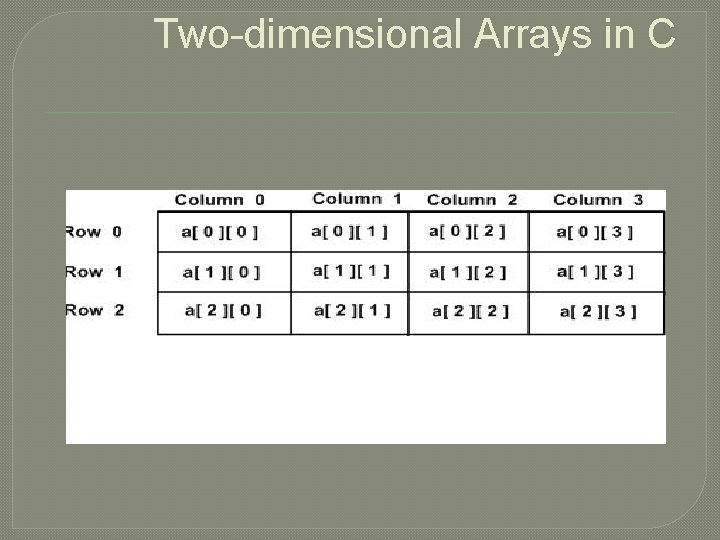
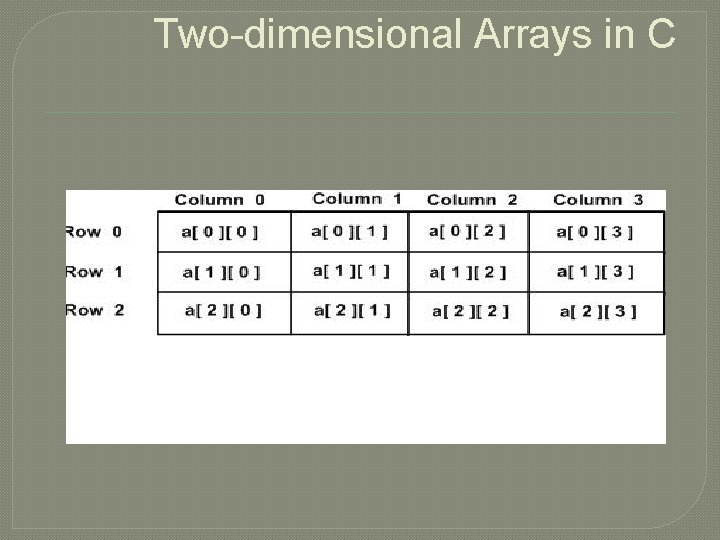
Two-dimensional Arrays in C �multidimensional array is the two-dimensional array �type array. Name [ x ][ y ];

Two-dimensional Arrays in C

�Initializing Two-Dimensional Arrays int a[3][4] = { {0, 1, 2, 3} , /* initializers for {4, 5, 6, 7} , {8, 9, 10, 11} /* initializers for row indexed by 2 */ };

�Accessing Two-Dimensional Array Elements int val = a[2][3];

Three-dimensional Arrays in C �For example, the following declaration creates a three dimensional integer array − �Ex-int threedim[5][10][4];

Passing Arrays as Function Arguments in C �void my. Function(int param[10]) {. . . //Statement Excution }

Abstract Data Type �ADT is useful tool for specifying the logical properties of a data type. �A data type is a collection of values & the set of operations on the values. �ADT refers to the mathematical concept that defines the data type. �ADT is not concerned with implementation but is useful in making use of data type.

ADT for an array �Arrays are stored in consecutive set of memory locations. �Array can be thought of as set of index and values. �For each index which is defined there is a value associated with that index. �There are two operations permitted on array data structure. retrieve and store

ADT for an array �CREATE()-produces empty array. �RETRIVE(array, index)->value Takes as input array and index and either returns appropriate value or an error. �STORE(array, index, value)-array used to enter new index value pairs.

Introduction to arrays Representation and analysis Type variable_name[size] Operations with arrays: Copy Delete Insert Search Sort Merging of sorting arrays.

Copy operation � � � � #include <stdio. h> int main() { int a[100], b[100] position, c n; printf("Enter number of elements in arrayn"); scanf("%d", &n); printf("Enter %d elementsn", n); for ( c = 0 ; c < n ; c++ ) scanf("%d", &a[c]); � printf("Enter %d elementsn", n); � � � for( c = 0 ; c < n - 1 ; c++ ) printf("%dn", a[c]); � //Coping the element of array a to b � � for( c = 0 ; c < n - 1 ; c++ ) { b[c]=a[c]; } � � } return 0; }

� � Enter number of elements in array -4 Enter 4 elements 1 � 2 � 3 � 4 � � � displaying array a 1 2 3 4 displaying array b 1 2 3 4 � Output

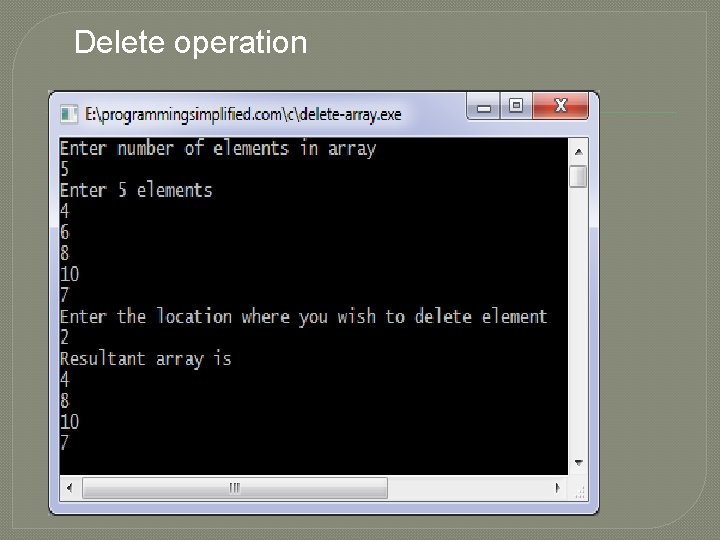
Delete operation � � � � � #include <stdio. h> int main() { int array[100], position, i, n; printf("Enter number of elements in arrayn"); scanf("%d", &n); printf("Enter %d elementsn", n); for ( i = 0 ; i < n ; i++ ) scanf("%d", &array[i]); printf("Enter the location where you wish to delete elementn"); scanf("%d", &position); � for ( i = position ; i < n; i++ ) • { � array[i] = array[i+1]; � � } printf("Resultant array isn"); for( i = 0 ; i < n-1 ; i++ ) � � � printf("%dn", array[i]); return 0; }

Delete operation

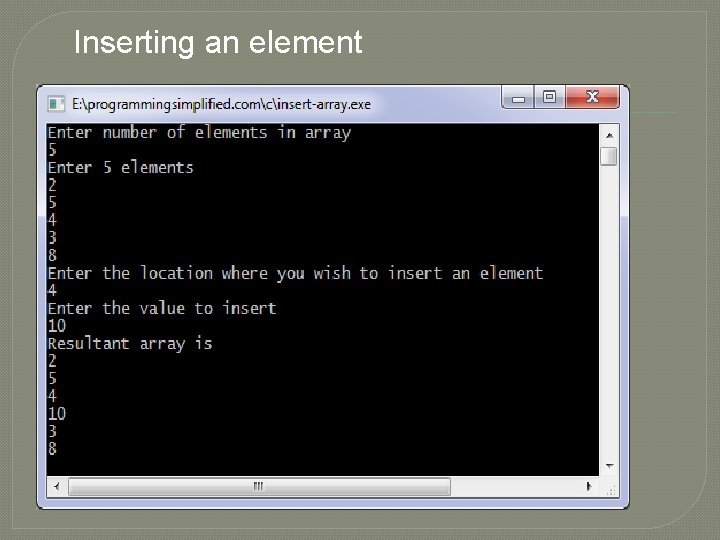
Inserting an element #include <stdio. h> int main() { int array[100], position, i, n, value; printf("Enter number of elements in arrayn"); scanf("%d", &n); printf("Enter %d elementsn", n); for (i= 0; i< n; i++) scanf("%d", &array[i]); printf("Enter the location where you wish to insert an elementn"); scanf("%d", &position); printf("Enter the value to insertn"); scanf("%d", &value); for (i = n - 1; i >= position ; i--) array[i+1] = array[i]; array[position] = value; printf("Resultant array isn"); for (i= 0; i <= n; i++) printf("%dn", array[i]); return 0; }

Inserting an element

Sort an array Int a[10]={5, 4, 3, 2, 1} for(i=0; i<n-1; i++) { for(j=0; j<=n-1; j++) { if(a[j]>a[j+1]) { temp=a[i]; a[i]=a[j]; a[j]=temp; } }

Reverse array #include <stdio. h> int main() { int array[100], n, i, temp, end; scanf("%d", &n); end = n - 1; for (i = 0; i < n; i++) { scanf("%d", &array[i]); } for (i= 0; < n/2; i++) { t emp = array[i]; array[i] = array[end]; array[end] = temp; end--; } printf("Reversed array elements are: n"); for ( i= 0; i < n; i++) { printf("%dn", array[i]); } return 0; }

Sort element using array int a[10]={5, 4, 3, 2, 1} for(i=0; i<n; i++) for(j=i+1; j<n; j++) { if(a[i]>a[j]) { temp=a[i]; a[i]=a[j]; a[j]=temp; } }

Merging of two arrays

Two-dimensional Arrays in C �multidimensional array is the two-dimensional array �type array. Name [ x ][ y ];

Two-dimensional Arrays in C

m-no of rows � n-no of columns � Printf(“n Enter the rows and columns”); � Scanf(%d %d”, &m, &n); � for(i=0; i<m; i++) �{ � • for(j=0; j<n; j++) • { �Printf(“n Enter the value of(%d)=“, i, j); �Scanf(“%d”, &a[i][j]); • }

� int main () { /* an array with 5 rows and 2 columns*/ � int a[5][2] = { {0, 0}, {1, 2}, {2, 4}, {3, 6}, {4, 8}}; � int i, j; � /* output each array element's value */ � for ( i = 0; i < 5; i++ ) � { � for ( j = 0; j < 2; j++ ) � { � printf("a[%d] = %dn", i, j, a[i][j] ); � } � return 0; �} �

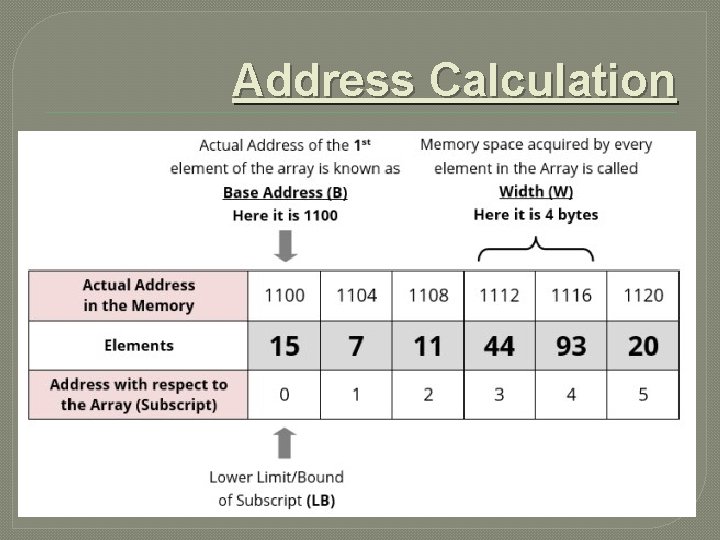
�Address Calculation in single (one) Dimension Array:

Address Calculation

Address Calculation � Array of an element of an array say “A[ I ]” is calculated using the following formula: � Address of A [ I ] = B + W * ( I – LB ) � Where, B = Base address W = Storage Size of one element stored in the array (in byte) I = Subscript of element whose address is to be found LB = Lower limit / Lower Bound of subscript, if not specified assume 0 (zero)

Address Calculation � Ex-Given the base address of an array B[1300…. . 1900] as 1020 and size of each element is 2 bytes in the memory. Find the address of B[1700]. Solution: � The given values are: B = 1020, LB = 1300, W = 2, I = 1700 � Address of A [ I ] = B + W * ( I – LB ) � = 1020 + 2 * (1700 – 1300) = 1020 + 2 * 400 = 1020 + 800 = 1820 [Ans]

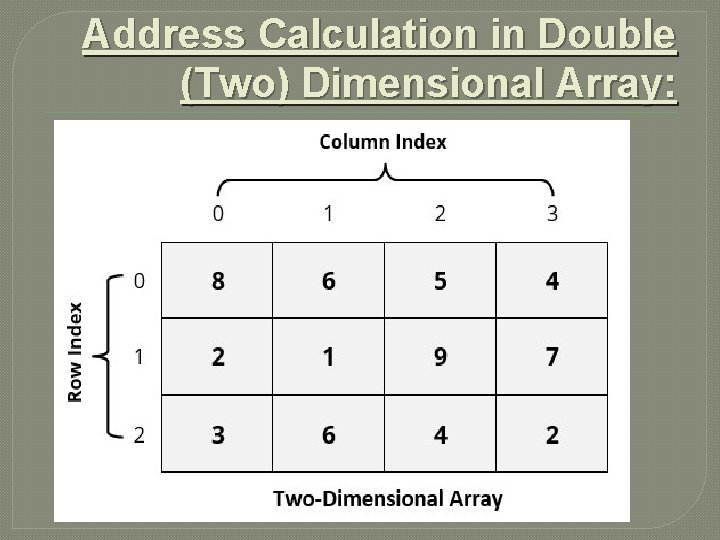
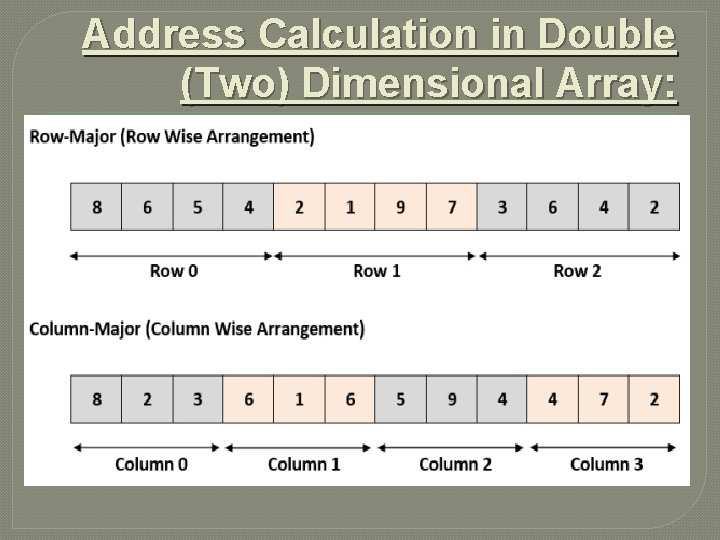
Address Calculation in Double (Two) Dimensional Array: �While storing the elements of a 2 -D array in memory, these are allocated contiguous memory locations. Therefore, a 2 -D array must be liberalized so as to enable their storage. There are two alternatives to achieve linearization: Row-Major and Column-Major.

Address Calculation in Double (Two) Dimensional Array:

Address Calculation in Double (Two) Dimensional Array:

Address Calculation in Double (Two) Dimensional Array: Address of an element of any array say “A[ I ][ J ]” is calculated in two forms as given: (1) Row Major System (2) Column Major System

Address Calculation in Double (Two) Dimensional Array: The address of a location in Row Major System is calculated using the following formula: Address of A [ I ][ J ] = B + W * [ N * ( I – Lr ) + ( J – Lc )

Address Calculation in Double (Two) Dimensional Array: The address of a location in Row Major System is calculated using the following formula: Address of A [ I ][ J ] = B + W * [ N * ( I – Lr ) + ( J – Lc ) B = Base address I = Row subscript of element whose address is to be found J = Column subscript of element whose address is to be found W = Storage Size of one element stored in the array (in byte) Lr = Lower limit of row/start row index of matrix, if not given assume 0 (zero) Lc = Lower limit of column/start column index of matrix, if not given assume 0 (zero) M = Number of row of the given matrix N = Number of column of the given matrix

Address Calculation in Double (Two) Dimensional Array: Column Major System: The address of a location in Column Major System is calculated using the following formula: Address of A [ I ][ J ] Column Major Wise = B + W * [( I – Lr ) + M * ( J – Lc )] B = Base address I = Row subscript of element whose address is to be found J = Column subscript of element whose address is to be found W = Storage Size of one element stored in the array (in byte) Lr = Lower limit of row/start row index of matrix, if not given assume 0 (zero) Lc = Lower limit of column/start column index of matrix, if not given assume 0 (zero) M = Number of row of the given matrix N = Number of column of the given matrix

Address Calculation in Double (Two) Dimensional Array: Important : Usually number of rows and columns of a matrix are given ( like A[20][30] or A[40][60] ) but if it is given as A[Lr- – – Ur, Lc- – – Uc]. In this case number of rows and columns are calculated using the following methods: Number of rows (M) will be calculated as = (Ur – Lr) + 1 Number of columns (N) will be calculated as = (Uc – Lc) + 1 And rest of the process will remain same as per requirement (Row Major Wise or Column Major Wise).

Address Calculation in Double (Two) Dimensional Array: Examples: Q 1. An array X [-15………. 10, 15…………… 40] requires one byte of storage. If beginning location is 1500 determine the location of X [15][20]. Solution: As you see here the number of rows and columns are not given in the question. So they are calculated as: Number or rows say M = (Ur – Lr) + 1 = [10 – (- 15)] +1 = 26 Number or columns say N = (Uc – Lc) + 1 = [40 – 15)] +1 = 26

Address Calculation in Double (Two) Dimensional Array: (i) Column Major Wise Calculation of above equation The given values are: B = 1500, W = 1 byte, I = 15, J = 20, Lr = -15, Lc = 15, M = 26 Address of A [ I ][ J ] =B + W * [ ( I – Lr ) + M * ( J – Lc ) ] = 1500 + 1 * [(15 – (-15)) + 26 * (20 – 15)] = 1500 + 1 * [30 + 26 * 5] = 1500 + 1 * [160] = 1660 [Ans]

Address Calculation in Double (Two) Dimensional Array: (ii) Row Major Wise Calculation of above equation The given values are: B = 1500, W = 1 byte, I = 15, J = 20, Lr = -15, Lc = 15, N = 26 Address of A [ I ][ J ] = B + W * [ N * ( I – Lr ) + ( J – Lc ) ] = 1500 + 1* [26 * (15 – (-15))) + (20 – 15)] = 1500 + 1 * [26 * 30 + 5] = 1500 + 1 * [780 + 5] = 1500 + 785 = 2285 [Ans]

Merging of two arrays � � � � int main() { int arr 1[30], arr 2[30], res[60]; int i, j, k, n 1, n 2; printf("n. Enter no of elements in 1 st array : "); scanf("%d", &n 1); � � � � for (i = 0; i < n 1; i++) { scanf("%d", &arr 1[i]); } printf("n. Enter no of elements in 2 nd array : "); scanf("%d", &n 2); � � � � � for (i = 0; i < n 2; i++) { scanf("%d", &arr 2[i]); } i = 0; j = 0; k = 0;

Merging of two arrays � // Merging starts � while (i < n 1 && j < n 2) � { � if (arr 1[i] <= arr 2[j]) � { � res[k] = arr 1[i]; � i++; � k++; � } � else � { res[k] = arr 2[j]; k++; j++; � } �} �

Merging of two arrays �/* Some elements in array 'arr 1' are still remaining � � where as the array 'arr 2' is exhausted */ while (i < n 1) � { � res[k] = arr 1[i]; � i++; � k++; � } �

Merging of two arrays �/* Some elements in array 'arr 2' are still remaining where as the array 'arr 1' is exhausted */ � � while (j < n 2) { res[k] = arr 2[j]; k++; j++; } � � �

Merging of two arrays //Displaying elements of array 'res' printf("n. Merged array is : "); for (i = 0; i < n 1 + n 2; i++) printf("%d ", res[i]); return (0); }

Merging of two arrays /* Some elements in array 'arr 2' are still remaining where as the array 'arr 2' is exhausted */ while (i < n 2) { res[k] = arr 2[i]; i++; k++; } for(i=0; i<k; i++) { printf(“%d”, res[i]); }

Merging of two arrays Output: Enter no of elements in 1 st array : 4 11 22 33 44 Enter no of elements in 2 nd array : 3 10 40 80 Merged array is : 10 11 22 33 40 44 80