Linear coord geometry KUS objectives BAT explore gradients

Linear coord geometry • KUS objectives BAT explore gradients of parallel and perpendicular line BAT rearrange and find equations of lines Starter: Ten questions Identify the equation of each of the following line graphs on the next page

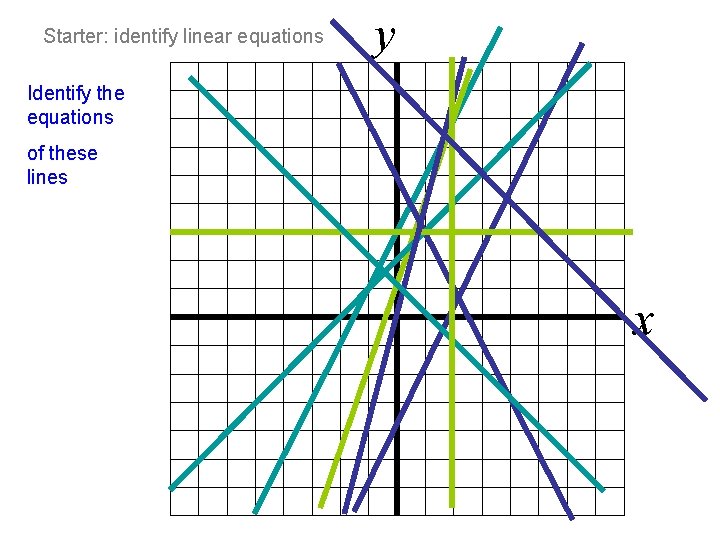
Starter: identify linear equations y Identify the equations of these lines x

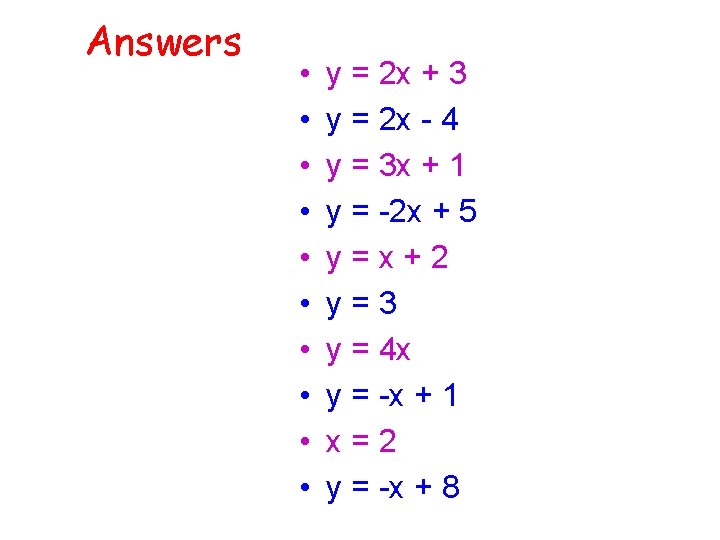
Answers • • • y = 2 x + 3 y = 2 x - 4 y = 3 x + 1 y = -2 x + 5 y=x+2 y=3 y = 4 x y = -x + 1 x=2 y = -x + 8

Notes: General equation of a line We are used to: • gradient y-intercept Another ‘standard way to write the equation of a line is: The General form of the equation of a line

WB 1 Gradient and y- intercept For each of these equations, i) rearrange it into the form y = mx + c ii) give the gradient iii) give the intercept on the y-axis. Gradient m = -2 Intercept (0, 10) 10 Gradient m = 2. 5 Intercept (0, 3) 3

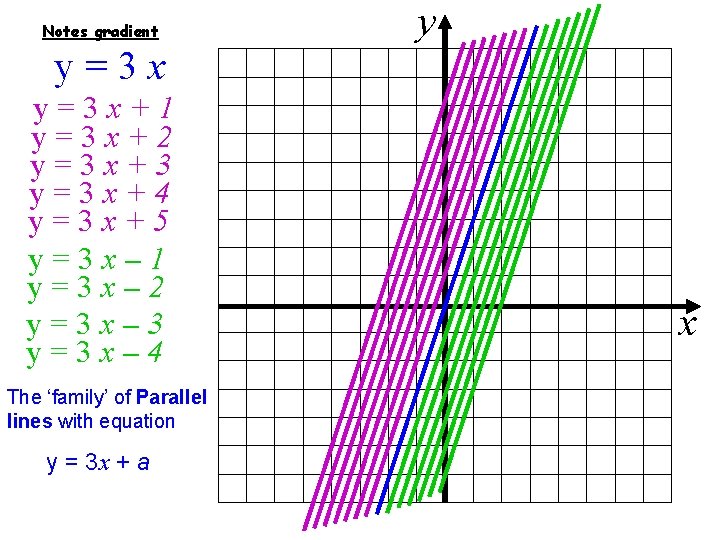
Notes gradient y y=3 x+1 y=3 x+2 y=3 x+3 y=3 x+4 y=3 x+5 y=3 x– 1 y=3 x– 2 y=3 x– 3 y=3 x– 4 The ‘family’ of Parallel lines with equation y = 3 x + a x

WB 2 There are three sets of parallel lines here. Match them up and say what the gradient is for each set.

Notes: General equation intersection points Why bother with the general equation? Solve these simultaneous equations: At times they are easier to work with:

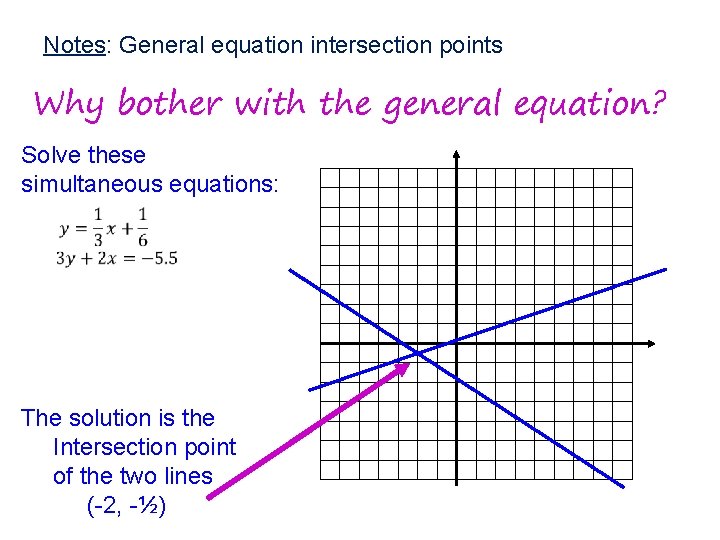
Notes: General equation intersection points Why bother with the general equation? Solve these simultaneous equations: The solution is the Intersection point of the two lines (-2, -½)

WB 3 • Which of these lines are parallel to the line 3 x - 2 y – 4 = 0

Notes These lines are perpendicular

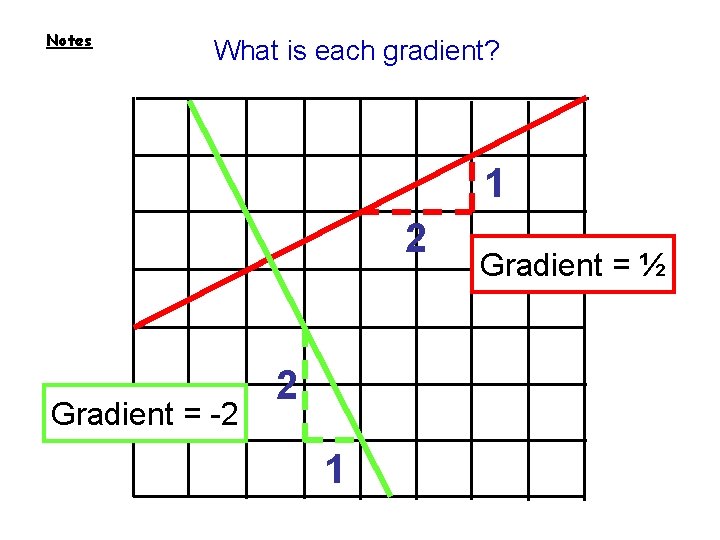
Notes What is each gradient? 1 2 Gradient = -2 2 1 Gradient = ½

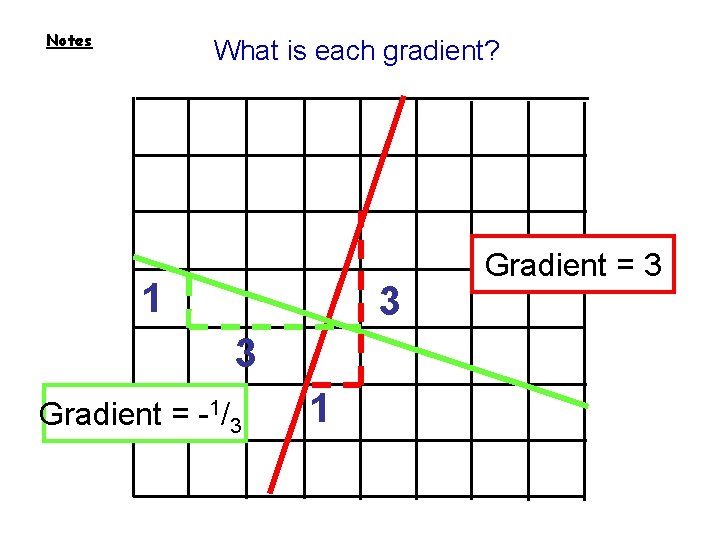
Notes What is each gradient? 1 3 3 Gradient = -1/3 1 Gradient = 3

Notes 1 THE GRADIENT OF A PERPENDICULAR LINE IS THE NEGATIVE RECIPROCAL OF THE OTHER

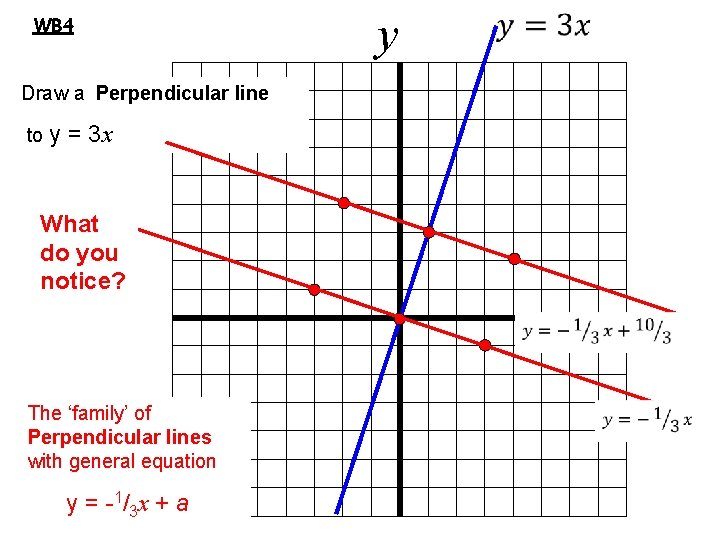
WB 4 y • Draw a Perpendicular line to y = 3 x What do you notice? The ‘family’ of Perpendicular lines with general equation y = - 1/ 3 x + a x

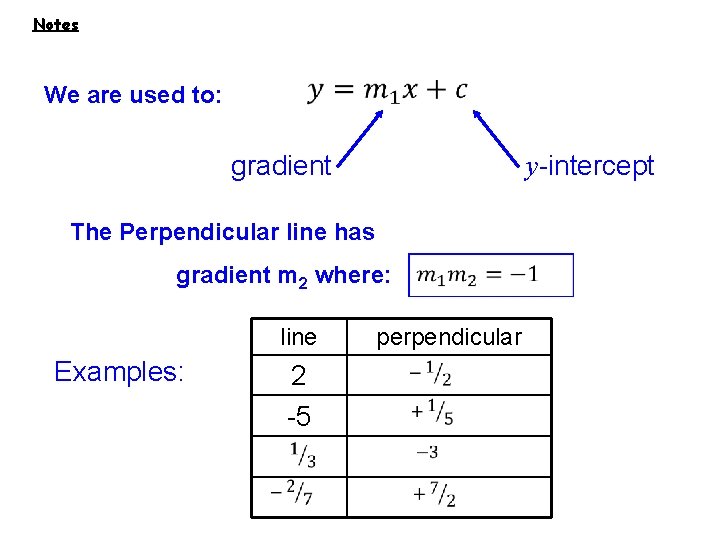
Notes We are used to: • gradient y-intercept The Perpendicular line has gradient m 2 where: line Examples: 2 -5 perpendicular

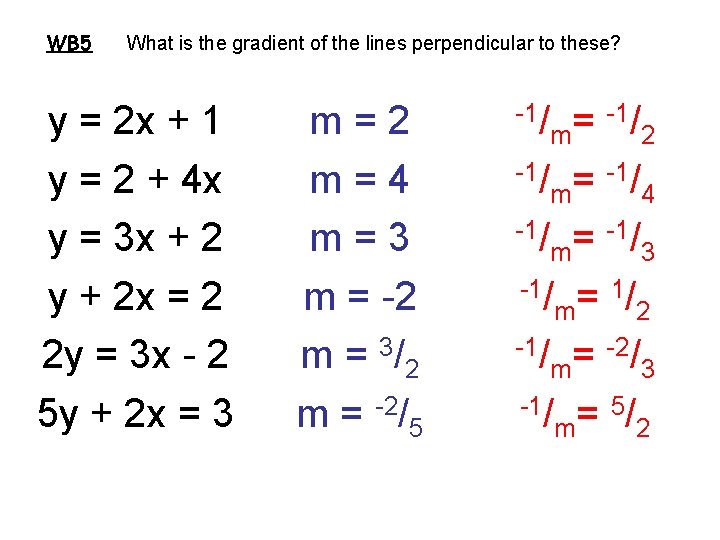
WB 5 What is the gradient of the lines perpendicular to these? y = 2 x + 1 y = 2 + 4 x y = 3 x + 2 y + 2 x = 2 2 y = 3 x - 2 5 y + 2 x = 3 m=2 m=4 m=3 m = -2 m = 3/ 2 m = -2/5 -1/ = m 2 -1/ = -1/ m 4 -1/ = -1/ m 3 -1/ = 1/ m 2 -1/ = -2/ m 3 -1/ = 5/ m 2

Has gradient m 1 = -2 So the gradient of a perpendicular line is m 2 = ½ When x = 4, y = 9 … so

Has gradient m 1 = -1/5 So the gradient of a perpendicular line is mnormal = 5 When x = 3/5, y = 7 … so

2 nd the gradient of line AB is So the perpendicular gradient is When x =-2, y = 4 so Is the perpendicular bisector of line AB

KUS objectives BAT explore gradients of parallel and perpendicular line BAT rearrange and find equations of lines self-assess One thing learned is – One thing to improve is –

END