Linear Combinations Given vectors is a linear combination

Linear Combinations Given vectors is a linear combination of Example: REVIEW and given scalars with weights

A vector equation REVIEW has the same solution set as the linear system whose augmented matrix is can be generated by a linear combination of vectors in if and only if the following linear system is consistent:

REVIEW Definition If combinations of Span subset of , then the set of all linear is denoted by and is called the spanned by
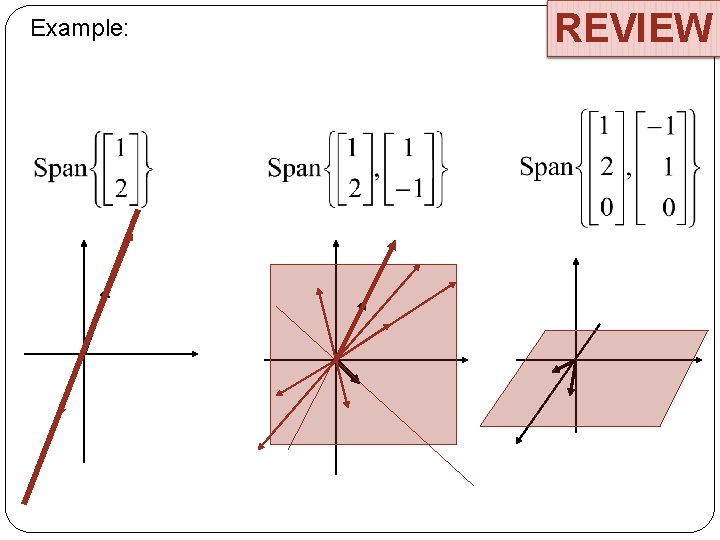
Example: REVIEW

1. 4 The Matrix Equation

Key Idea We will see how think of a linear combination of vectors as a product of a matrix and a vector.

Linear Combinations is a linear combination of the columns of A with corresponding entries in x as weights. Note: is defined only if the number of columns of A equals the number of elements in.
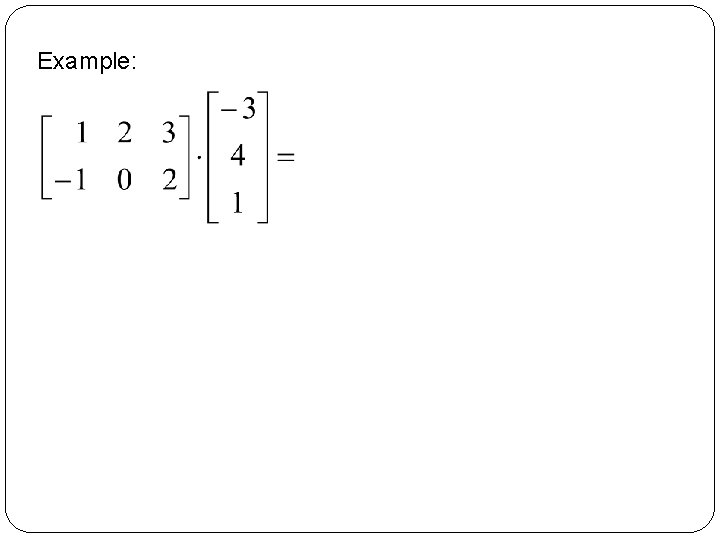
Example:

Compute

A matrix equation has the same solution set as the vector equation which has the same solution set as the linear system whose augmented matrix is Therefore: Ax = b has a solution if and only if b is a linear combination of columns of A

Theorem 4: The following statements are equivalent: 1. For each vector b, the equation has a solution. 2. Each vector b is a linear combination of the columns of A. 3. The columns of A span 4. A has a pivot position in every row. 1. Note: Theorem 4 is about a coefficient matrix A, not an augmented matrix.

Row-Vector Rule for Computing If the product is defined, then the ith entry in is the sum of the products of corresponding entries from row i of A and from the vector x.

Theorem 5:
- Slides: 13