Linear Combination vs Common Divisor Greatest common divisor

Linear Combination vs Common Divisor Greatest common divisor d is a common divisor of a and b if d|a and d|b gcd(a, b) = greatest common divisor of a and b Smallest positive integer linear combination d is an integer linear combination of a and b if d=sa+tb for integers s, t. spc(a, b) = smallest positive integer linear combination of a and b Theorem: gcd(a, b) = spc(a, b)

Linear Combination vs Common Divisor Theorem: gcd(a, b) = spc(a, b) For example, the greatest common divisor of 52 and 44 is 4. And 4 is a linear combination of 52 and 44: 6 · 52 + (− 7) · 44 = 4 Furthermore, no linear combination of 52 and 44 is equal to a smaller positive integer. To prove theorem, we will prove: gcd(a, b) <= spc(a, b) gcd(a, b) | spc(a, b) <= gcd(a, b) spc(a, b) is a common divisor of a and b

GCD <= SPC 3. If d | a and d | b, then d | sa + tb for all s and t. Proof of (3) d | a => a = dk 1 d | b => b = dk 2 sa + tb = sdk 1 + tdk 2 = d(sk 1 + tk 2) => d|(sa+tb) GCD | SPC Let d = gcd(a, b). By definition, d | a and d | b. Let f = spc(a, b) = sa+tb By (3), d | f. This implies d <= f. That is gcd(a, b) <= spc(a, b).

SPC <= GCD We will prove that spc(a, b) is actually a common divisor of a and b. First, show that spc(a, b) | a. 1. Suppose, by way of contradiction, that spc(a, b) does not divide a. 2. Then, by the Division Theorem, 3. a = q x spc(a, b) + r and spc(a, b) > r > 0 4. Let spc(a, b) = sa + tb. 5. So r = a – q x spc(a, b) = a – q x (sa + tb) = (1 -qs)a + qtb. 6. Thus r is an integer linear combination of a and b, and spc(a, b) > r. 7. This contradicts the definition of spc(a, b), and so r must be zero. Similarly, spa(a, b) | b. So, spc(a, b) is a common divisor of a and b, thus by definition spc(a, b) <= gcd(a, b).

Extended GCD Algorithm How can we write gcd(a, b) as an integer linear combination? This can be done by extending the Euclidean’s algorithm. Example: a = 259, b=70 259 = 3· 70 + 49 49 = a – 3 b 70 = 1· 49 + 21 21 = 70 - 49 21 = b – (a-3 b) = -a+4 b 49 = 2· 21 + 7 7 = 49 - 2· 21 7 = (a-3 b) – 2(-a+4 b) = 3 a – 11 b 21 = 7· 3 + 0 done, gcd = 7

Extended GCD Algorithm Example: a = 899, b=493 899 = 1· 493 + 406 493 = 1· 406 + 87 so 406 = a - b so 87 = 493 – 406 = b – (a-b) = -a + 2 b 406 = 4· 87 + 58 so 58 = 406 - 4· 87 = (a-b) – 4(-a+2 b) = 5 a - 9 b 87 = 1· 58 + 29 so 29 = 87 – 1· 58 = (-a+2 b) - (5 a-9 b) = -6 a + 11 b 58 = 2· 29 + 0 done, gcd = 29

This Lecture • Quotient remainder theorem • Greatest common divisor & Euclidean algorithm • Linear combination and GCD, extended Euclidean algorithm • Prime factorization and other applications

Application of the Theorem: gcd(a, b) = spc(a, b) Why is theorem useful? (1) we can now “write down” gcd(a, b) as some concrete equation, (i. e. gcd(a, b) = sa+tb for some integers s and t), and this allows us to reason about gcd(a, b) much easier. (2) If we can find integers s and t so that sa+tb=c, then we can conclude that gcd(a, b) <= c. In particular, if c=1, then we can conclude that gcd(a, b)=1.

Prime Divisibility Theorem: gcd(a, b) = spc(a, b) Lemma: p prime and p|a·b implies p|a or p|b. pf: say p does not divide a. so gcd(p, a)=1. So by the Theorem, there exist s and t such that sa + tp =1 (sa)b + (tp)b = b p|ab p|p Hence p|b Cor : If p is prime, and p| a 1·a 2···am then p|ai for some i.

Fundamental Theorem of Arithmetic Every integer, n>1, has a unique factorization into primes: p 0 ≤ p 1 ≤ ··· ≤ pk p 0 p 1 ··· pk = n Example: 61394323221 = 3· 3· 3· 7· 11· 37· 37· 53

Unique Factorization Theorem: There is a unique factorization. proof: suppose, by contradiction, that there are numbers with two different factorization. By the well-ordering principle, we choose the smallest such n >1: n = p 1·p 2···pk = q 1·q 2···qm Since n is smallest, we must have that pi qj all i, j (Otherwise, we can obtain a smaller counterexample. ) Since p 1|n = q 1·q 2···qm, so by Cor. , p 1|qi for some i. contradiction! Since both p 1 = qi are prime numbers, we must have p 1 = qi.

Application of the Theorem: gcd(a, b) = spc(a, b) Lemma. If gcd(a, b)=1 and gcd(a, c)=1, then gcd(a, bc)=1. By the Theorem, there exist s, t, u, v such that sa + tb = 1 ua + vc = 1 Multiplying, we have (sa + tb)(ua + vc) = 1 Þ saua + savc + tbua + tbvc = 1 Þ (sau + svc + tbu)a + (tv)bc = 1 By the Theorem, since spc(a, bc)=1, we have gcd(a, bc)=1

Die Hard Simon says: On the fountain, there should be 2 jugs, do you see them? A 5 -gallon and a 3 -gallon. Fill one of the jugs with exactly 4 gallons of water and place it on the scale and the timer will stop. You must be precise; one ounce more or less will result in detonation. If you're still alive in 5 minutes, we'll speak.

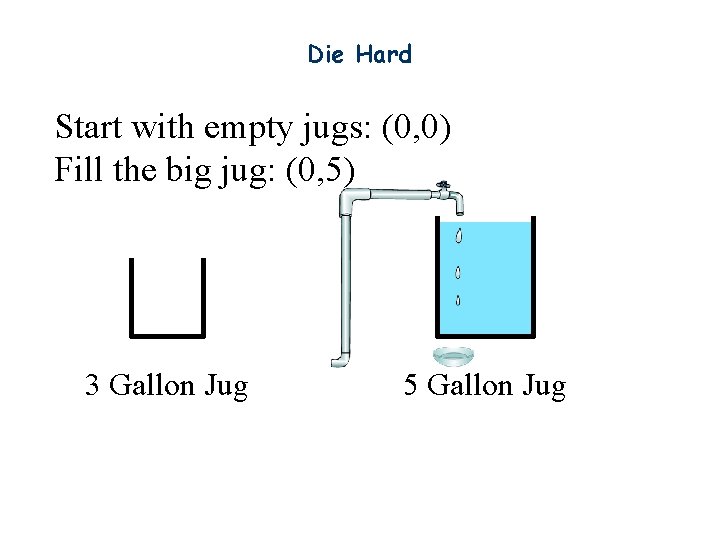
Die Hard Start with empty jugs: (0, 0) Fill the big jug: (0, 5) 3 Gallon Jug 5 Gallon Jug

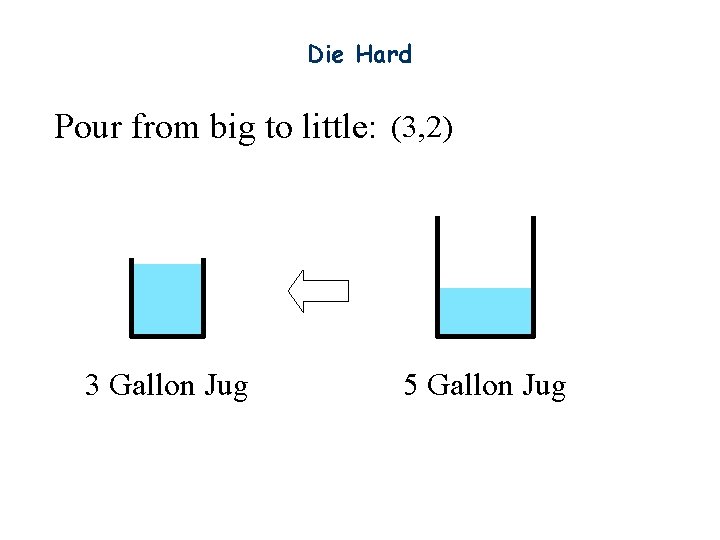
Die Hard Pour from big to little: (3, 2) 3 Gallon Jug 5 Gallon Jug

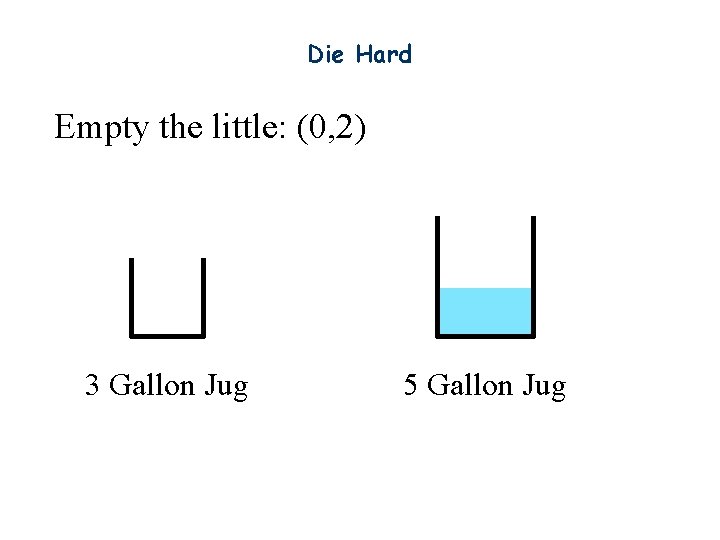
Die Hard Empty the little: (0, 2) 3 Gallon Jug 5 Gallon Jug

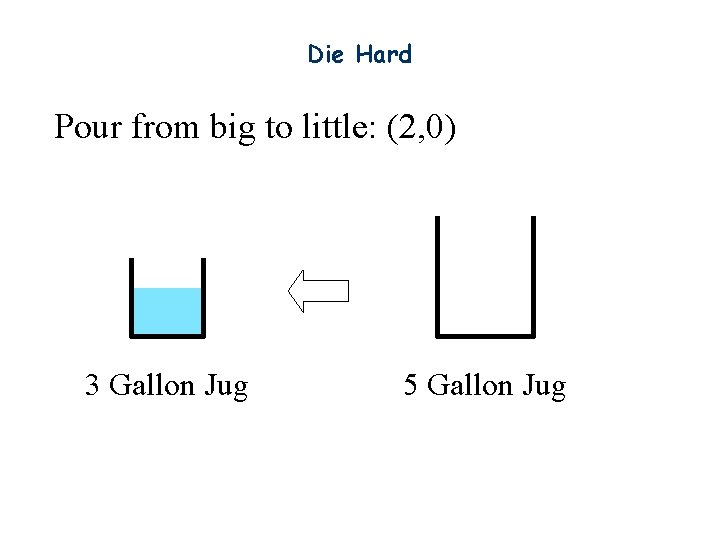
Die Hard Pour from big to little: (2, 0) 3 Gallon Jug 5 Gallon Jug

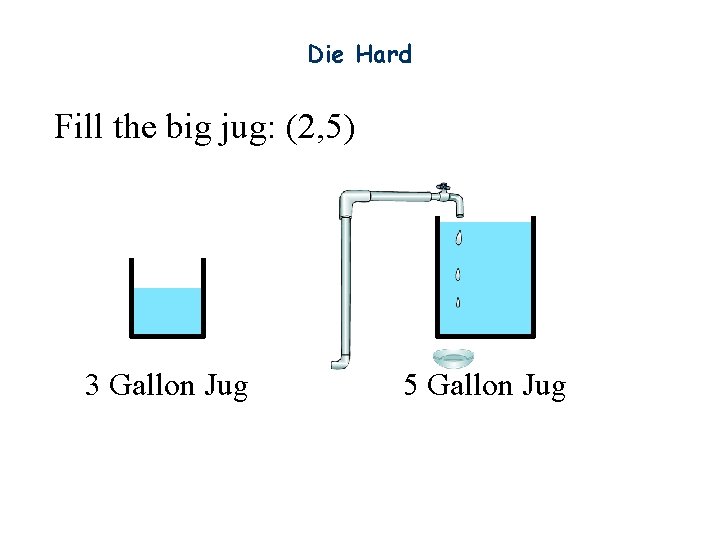
Die Hard Fill the big jug: (2, 5) 3 Gallon Jug 5 Gallon Jug

Die Hard Pour from big to little: (3, 4) 3 Gallon Jug 5 Gallon Jug Done!!

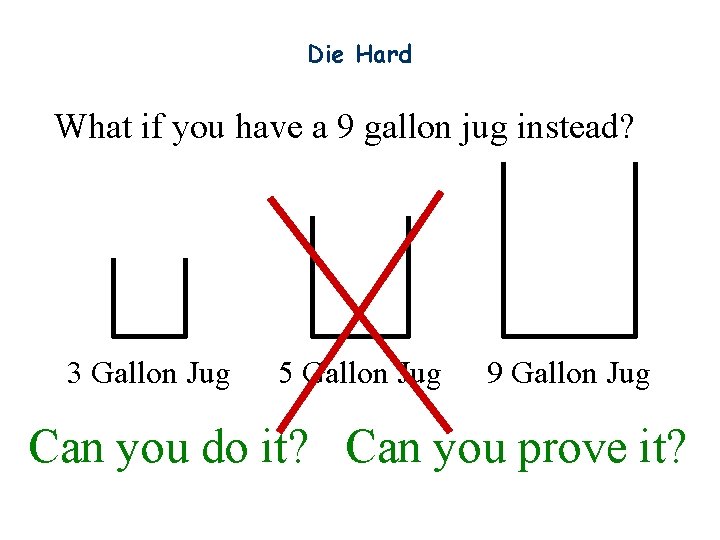
Die Hard What if you have a 9 gallon jug instead? 3 Gallon Jug 5 Gallon Jug 9 Gallon Jug Can you do it? Can you prove it?

Die Hard Supplies: 3 Gallon Jug Water 9 Gallon Jug

Invariant Method Invariant: the number of gallons in each jug is a multiple of 3. i. e. , 3|b and 3|l (3 divides b and 3 divides l) Corollary: it is impossible to have exactly 4 gallons in one jug. Bruce Dies!

Generalized Die Hard Can Bruce form 3 gallons using 21 and 26 -gallon jugs? This question is not so easy to answer without number theory.

General Solution for Die Hard Invariant in Die Hard Transition: Suppose that we have water jugs with capacities B and L. Then the amount of water in each jug is always an integer linear combination of B and L. Theorem: gcd(a, b) = spc(a, b) Corollary: Every linear combination of a and b is a multiple of gcd(a, b). Corollary: The amount of water in each jug is a multiple of gcd(a, b).

General Solution for Die Hard Corollary: The amount of water in each jug is a multiple of gcd(a, b). Given jug of 3 and jug of 9, is it possible to have exactly 4 gallons in one jug? NO, because gcd(3, 9)=3, and 4 is not a multiple of 3. Given jug of 21 and jug of 26, is it possible to have exactly 3 gallons in one jug? gcd(21, 26)=1, and 3 is a multiple of 1, so this possibility has not been ruled out yet. Theorem. Given water jugs of capacity a and b, it is possible to have exactly k gallons in one jug if and only if k is a multiple of gcd(a, b).

General Solution for Die Hard Theorem. Given water jugs of capacity a and b, it is possible to have exactly k gallons in one jug if and only if k is a multiple of gcd(a, b). Given jug of 21 and jug of 26, is it possible to have exactly 3 gallons in one jug? gcd(21, 26) = 1 Þ 5 x 21 – 4 x 26 = 1 Þ 15 x 21 – 12 x 26 = 3 Repeat 15 times: 1. Fill the 21 -gallon jug. 2. Pour all the water in the 21 -gallon jug into the 26 -gallon jug. Whenever the 26 -gallon jug becomes full, empty it out.

General Solution for Die Hard 15 x 21 – 12 x 26 = 3 Repeat 15 times: 1. Fill the 21 -gallon jug. 2. Pour all the water in the 21 -gallon jug into the 26 -gallon jug. Whenever the 26 -gallon jug becomes full, empty it out. 1. There must be exactly 3 gallons left after this process. 2. Totally we have filled 15 x 21 gallons. 3. We pour out some multiple t of 26 gallons. 4. The 26 gallon jug can only hold somewhere between 0 and 26. 5. So t must be equal to 12. 6. And there are exactly 3 gallons left.

General Solution for Die Hard Given two jugs with capacity A and B with A < B, the target is C. If gcd(A, B) does not divide C, then it is impossible. Otherwise, compute C = s. A + t. B. Repeat s times: 1. Fill the A-gallon jug. 2. Pour all the water in the A-gallon jug into the B-gallon jug. Whenever the B-gallon jug becomes full, empty it out. The B-gallon jug will be emptied exactly t times. After that, there will be exactly C gallons in the B-gallon jug.

Modular Arithmetic

This Lecture Modular arithmetic is an arithmetic about remainders. It is very useful in coding theory and cryptography. In this lecture we will focus on additions and multiplications, while in the next lecture we will talk about “divisions”. This lecture is short. We will talk about: • Basic rule of modular addition and modular multiplication • Applications: Fast exponentiation and fast division test

Modular Arithmetic Def: a b (mod n) iff n|(a - b) iff a mod n = b mod n. Be careful, a mod n means “the remainder when a is divided by n”. a b (mod n) means “a and b have the same remainder when divided by n”. e. g. 12 2 (mod 10) 12 mod 10 = 2 107 207 (mod 10) 207 mod 10 = 7 7 3 (mod 2) 7 mod 2 = 1 7 -1 (mod 2) -1 mod 2 = 1 13 -1 (mod 7) -1 mod 7 = 6 -15 10 (mod 5) -15 mod 5 = 0 Fact: a a mod n (mod n) as a and a mod n have the same remainder mod n Fact: if a b (mod n), then a = b + nx for some integer x.

Modular Addition Lemma: If a c (mod n), and b d (mod n) then a+b c+d (mod n). When you try to understand a statement like this, first think about the familiar cases, e. g. n=10 or n=2. When n=2, it says that if a and c have the same parity, and b and d have the same parity, then a+b and c+d have the same parity. When n=10, it says that if a and c have the same last digit, and b and d have the same last digit, then a+b and c+d have the same last digit. And the lemma says that the same principle applied for all n.

Modular Addition Lemma: If a c (mod n), and b d (mod n) then a+b c+d (mod n). Example 1 13 1 (mod 3), 25 1 (mod 3) => 12 + 25 (mod 3) 1 + 1 (mod 3) 2 (mod 3) Example 2 87 2 (mod 17), 222 1 (mod 17) => 87 + 222 (mod 17) 2 + 1 (mod 17) 3 (mod 17) Example 3 101 2 (mod 11), 141 -2 (mod 11) => 101 + 141 (mod 11) 0 (mod 11) In particular, when computing a+b mod n, we can first replace a by a mod n and b by b mod n, so that the computation is faster.

Modular Addition Lemma: If a c (mod n), and b d (mod n) then a+b c+d (mod n). Proof a c (mod n) => a = c + nx for some integer x b d (mod n) => b = d + ny for some integer y To show a+b c+d (mod n), it is equivalent to showing that n | (a+b-c-d). Consider a+b-c-d = (c+nx) + (d+ny) – c –d = nx + ny. It is clear that n | nx + ny. Therefore, n | a+b-c-d. We conclude that a+b c+d (mod n).

Modular Multiplication Lemma: If a c (mod n), and b d (mod n) then ab cd (mod n). Example 1 9876 6 (mod 10), 17642 2 (mod 10) => 9876 * 17642 (mod 10) 6 * 2 (mod 10) Example 2 10987 1 (mod 2), 28663 1 (mod 2) => 10987 * 28663 (mod 2) 1 (mod 2) Example 3 1000 -1 (mod 7), 1000000 1 (mod 7) => 1000 * 1000000 (mod 7) -1 * 1 (mod 7) -1 (mod 7) In particular, when computing ab mod n, we can first replace a by a mod n and b by b mod n, so that the computation is faster.

Modular Multiplication Lemma: If a c (mod n), and b d (mod n) then ab cd (mod n). Proof a c (mod n) => a = c + nx for some integer x b d (mod n) => b = d + ny for some integer y To show ab cd (mod n), it is equivalent to showing that n | (ab-cd). Consider ab-cd = (c+nx) (d+ny) – cd = cd + dnx + cny + n 2 xy – cd = n(dx + cy + nxy). It is clear that n | n(dx + cy + nxy). Therefore, n | ab-cd. We conclude that ab cd (mod n).

This Lecture • Basic rule of modular addition and modular multiplication • Applications: Fast exponentiation and fast division test

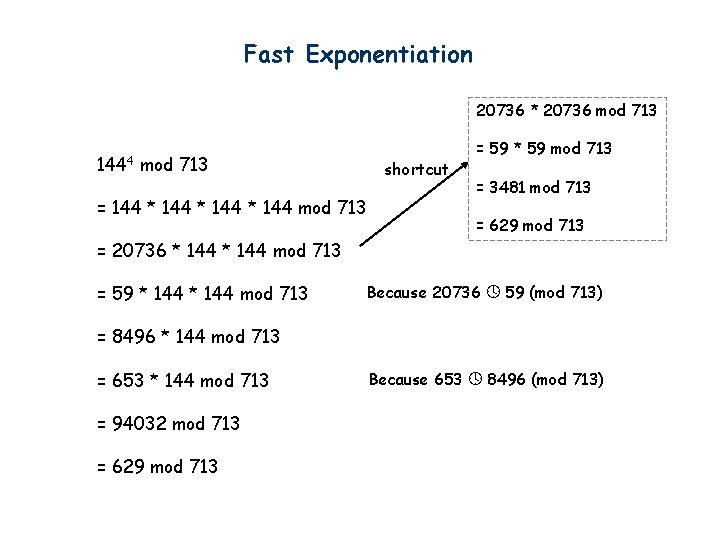
Fast Exponentiation 20736 * 20736 mod 713 1444 mod 713 shortcut = 144 * 144 mod 713 = 59 * 59 mod 713 = 3481 mod 713 = 629 mod 713 = 20736 * 144 mod 713 = 59 * 144 mod 713 Because 20736 59 (mod 713) = 8496 * 144 mod 713 = 653 * 144 mod 713 = 94032 mod 713 = 629 mod 713 Because 653 8496 (mod 713)

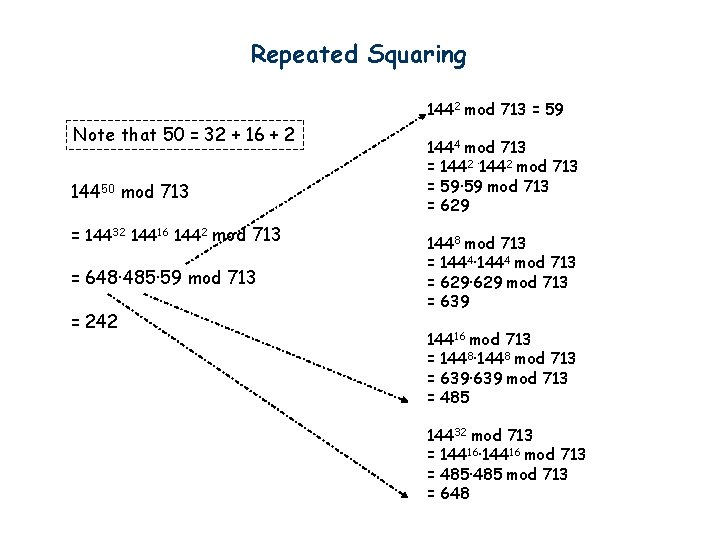
Repeated Squaring 1442 mod 713 = 59 Note that 50 = 32 + 16 + 2 14450 mod 713 = 14432 14416 1442 mod 713 = 648·485·59 mod 713 = 242 1444 mod 713 = 1442 ·1442 mod 713 = 59·59 mod 713 = 629 1448 mod 713 = 1444·1444 mod 713 = 629·629 mod 713 = 639 14416 mod 713 = 1448·1448 mod 713 = 639·639 mod 713 = 485 14432 mod 713 = 14416·14416 mod 713 = 485·485 mod 713 = 648

Fast Division Test Using the basic rules for modular addition and modular multiplication, we can derive some quick test to see if a big number is divisible by a small number. Suppose we are given the decimal representation of a big number N. To test if N is divisible by a small number n, of course we can do a division to check. But can we do faster? If n = 2, we just need to check whether the last digit of N is even or not. If n = 10, we just need to check whether the last digit of N is 0 or not. If n = 5, we just need to check whether the last digit of N is either 5 or 0 or not. What about when n=3? When n=7? When n=11?

Fast Division Test A number written in decimal divisible by 9 if and only if the sum of its digits is a multiple of 9? Example 1. 9333234513171 is divisible by 9. 9+3+3+3+2+3+4+5+1+3+1+7+1 = 45 is divisible by 9. Example 2. 128573649683 is not divisible by 9. 1+2+8+5+7+3+6+4+9+6+8+3 = 62 is not divisible by 9.

Fast Division Test Claim. A number written in decimal is divisible by 9 if and only if the sum of its digits is a multiple of 9. Hint: 10 1 (mod 9). Let the decimal representation of N be dkdk-1 dk-2…d 1 d 0. This means that N = dk 10 k + dk-110 k-1 + … + d 110 + d 0 Note that di 10 i mod 9 = (di) (10 i mod 9) mod 9 Rule of modular multiplication = (di) (10 mod 9) … (10 mod 9) mod 9 i terms = (di) (1 mod 9) … (1 mod 9) mod 9 = di mod 9

Fast Division Test Claim. A number written in decimal is divisible by 9 if and only if the sum of its digits is a multiple of 9. Hint: 10 1 (mod 9). Let the decimal representation of n be dkdk-1 dk-2…d 1 d 0. This means that N = dk 10 k + dk-110 k-1 + … + d 110 + d 0 Note that di 10 i mod 9 = di mod 9. Hence N mod 9 = (dk 10 k + dk-110 k-1 + … + d 110 + d 0) mod 9 Rule of modular addition = (dk 10 k mod 9 + dk-110 k-1 mod 9 + … + d 110 mod 9 + d 0 mod 9) mod 9 = (dk mod 9 + dk-1 mod 9 + … + d 1 mod 9 + d 0 mod 9) mod 9 = (dk + dk-1 + … + d 1 + d 0) mod 9 By previous slide

Fast Division Test The same procedure works to test whether N is divisible by n=3. What about n=11? Hint: 10 -1 (mod 11). Let the decimal representation of N be d 92 d 91 d 90…d 1 d 0 Then N is divisible by 11 if and only if d 92 -d 91+d 90…-d 1+d 0 is divisible by 11. What about n=7? Hint: 1000 -1 (mod 7). Why? Try to work it out.

Quick Summary Need to know how to apply the basic rules effectively. Understand the principle of fast division tests. Repeated squaring will be useful later.