Linear Best Fit Models Warm Up Problem of

Linear Best Fit Models Warm Up Problem of the Day Lesson Presentation Lesson Quizzes

Linear Best Fit Models Warm Up Describe a scatter plot representing data with the given characteristics. 1. A strong positive correlation or association between the two variables. Linear pattern of dots going upward from left to right. 2. A strong negative correlation or association between the two variables. Linear pattern of dots going downward from left to right.

Linear Best Fit Models Problem of the Day The temperature at the base of a Hawaiian mountain is 75 o F. For every 1000 -ft increase in elevation, the temperature drops by 10 o F. Describe the association or correlation between these two variables: temperature and elevation. negative

Linear Best Fit Models Learn to identify patterns in scatter plots, and informally fit and use a linear model to solve problems and make predictions as appropriate.

Linear Best Fit Models Vocabulary clustering

Linear Best Fit Models When data points in a scatter plot are grouped more in one part of the graph than another, it is called clustering. Clustering helps identify possible relationships between data.

Linear Best Fit Models Helpful Hint Be sure to consider outliers when making predictions or drawing conclusions from data. One outlier can greatly change some statistical measures.

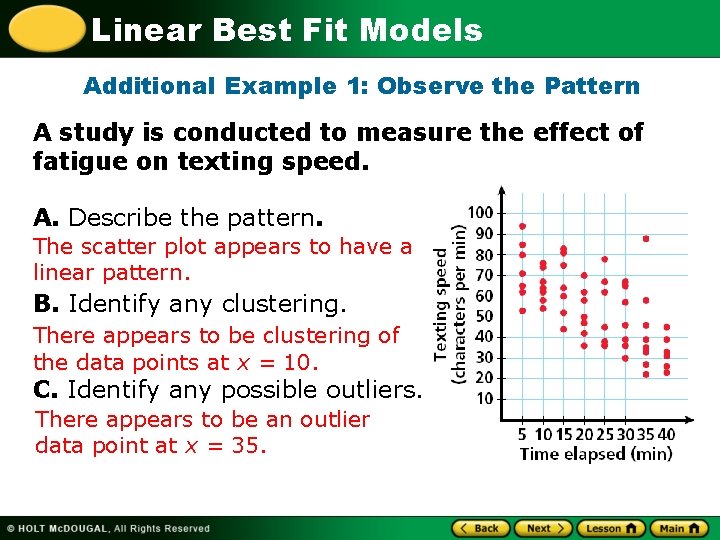
Linear Best Fit Models Additional Example 1: Observe the Pattern A study is conducted to measure the effect of fatigue on texting speed. A. Describe the pattern. The scatter plot appears to have a linear pattern. B. Identify any clustering. There appears to be clustering of the data points at x = 10. C. Identify any possible outliers. There appears to be an outlier data point at x = 35.

Linear Best Fit Models Check It Out: Example 1 The sales of fruit bars are shown in the scatter plot. A. Describe the pattern. The scatter plot appears to have a linear pattern. B. Identify any clustering. There appears to be an outlier data point at x = 1. C. Identify any possible outliers. There appears to be clustering of the data points at x = 0. 25.

Linear Best Fit Models Additional Example 2: Assessing the Line of Best Fit Compare the given scatter plots of data and their lines of best fit. Tell which model better fits the data. Explain your answer. Both scatter plots show data sets that have a positive correlation. The points in Graph A are closer to the line of best fit than in Graph B. The points are closer and more evenly divided both above and below the line of best fit.

Linear Best Fit Models Check It Out: Example 2 Compare the given scatter plots of data and their lines of best fit. Tell which model better fits the data. Explain your answer. Graph A has a negative correlation and Graph B has a positive correlation. The points in Graph A are closer to the line of best fit than in Graph B.

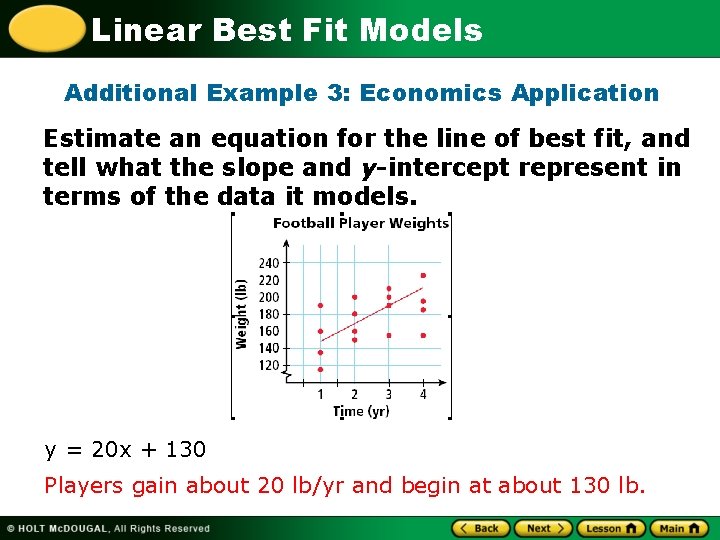
Linear Best Fit Models Additional Example 3: Economics Application Estimate an equation for the line of best fit, and tell what the slope and y-intercept represent in terms of the data it models. y = 20 x + 130 Players gain about 20 lb/yr and begin at about 130 lb.

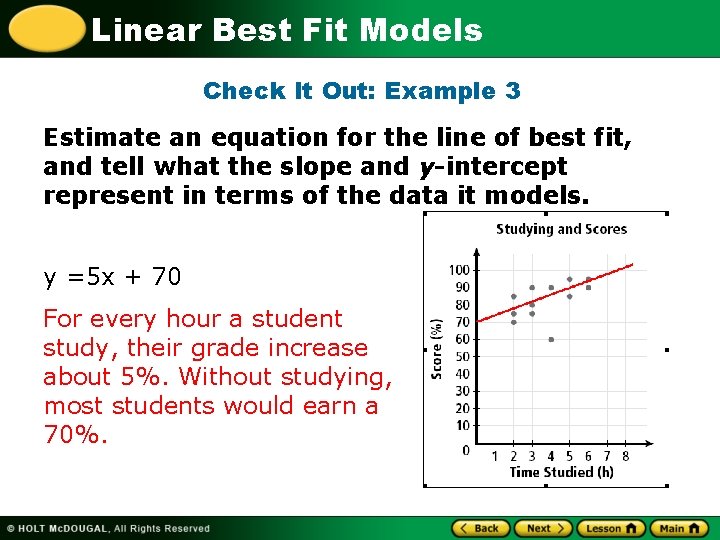
Linear Best Fit Models Check It Out: Example 3 Estimate an equation for the line of best fit, and tell what the slope and y-intercept represent in terms of the data it models. y =5 x + 70 For every hour a student study, their grade increase about 5%. Without studying, most students would earn a 70%.

Linear Best Fit Models Lesson Quizzes Standard Lesson Quiz for Student Response Systems

Linear Best Fit Models Lesson Quiz Use the scatter plot for Items 1– 4. 1. Does the pattern of association between the two variables appear to be linear or nonlinear? linear 2. Identify any clustering. none 3. Identify any possible outliers. x=3

Linear Best Fit Models Lesson Quiz Use the scatter plot for Items 1– 4. 4. Find an equation for the line of best fit, and tell what the slope and intercept represent. y = -3 x + 55. For each month on the diet, the dogs lost an average of 3 lb. On average, the dogs began at a weight of 55 lb.

Linear Best Fit Models Lesson Quiz for Student Response Systems 1. Does the pattern of association between the two variables appear to be linear or nonlinear? . A. Linear B. Nonlinear 2. Identify any possible outliers. A. x = 0. 25 B. x = 0. 75 C. x = 1 D. x = 100