Linear and Nonlinear Lattice Correction Via Betatron Phase

Linear and Nonlinear Lattice Correction Via Betatron Phase NOCE Workshop W. Guo, E. Blum Sep. 21, 2017 1 BROOKHAVEN SCIENCE

Outline 1. Introduction to the NSLS-II 2. The concept of phase correction 3. 1 mr resolution and application to NSLS-II linear lattice 4. Nonlinear correction scheme 5. Nonlinear correction results and validation 6. Summary 2 BROOKHAVEN SCIENCE

NSLS-II Layout and Main Parameters 200 Me. V Linac 15 n. C/160 -300 ns dp/p=0. 5% , ε=50 µm rad Storage Ring Main Parameters C. L (straights) 9. 3 m 3 Ge. V Booster 158 m, 20 m. A 1 Hz, dp/p=0. 08%, ε =40 nm rad 30 -cell storage ring NSLS-II schematic 792 m frf 6. 6 & MHz Εx/y (w. DW) 0. 9 nm/10 pm αc. 00037 ρ 25 m 499. 68 f (landau) GHz 1. 5 h 1320 Vrf 4. 8 MV σl 11. 5 ps Q (bunch) 1. 2 n. C I (total) 500 m. A t (Touschek) >3 hrs U (w. DW) 0. 675 Me. V f (Top-Off) 1/min σδ (w. DW) 0. 094% 3 Stability BROOKHAVEN Δx/y<0. 1 σ SCIENCE

Operation Status • • • Construction started in FY 08 Commissioning of the SR started in April 2014 Operation started in October 2014 Reliability has achieved >90%, user time is close to 5000 hours There about 15 beam lines operating on a daily basis. In 2016 there were about 1000 unique users. 4 BROOKHAVEN SCIENCE

The Concept of Phase Correction Oscillation at BPM , θ=2πn Define the phase advance eror: Quadrupole strength correction Response matrix Measured phase error Benefit 1. Fast measurement 2. Independent of BPM gain and tilt 5 BROOKHAVEN SCIENCE

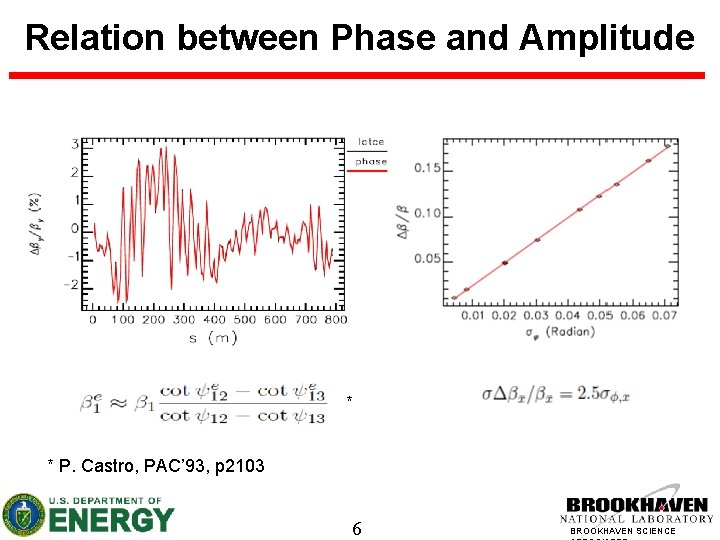
Relation between Phase and Amplitude * * P. Castro, PAC’ 93, p 2103 6 BROOKHAVEN SCIENCE

Improved Phase Calculation Fourier Transform For signal x(n), n=1, 2, 3, …. N New Method 1. Naff fit for the frequency; 2. fit for the phase: Analytically: 7 BROOKHAVEN SCIENCE

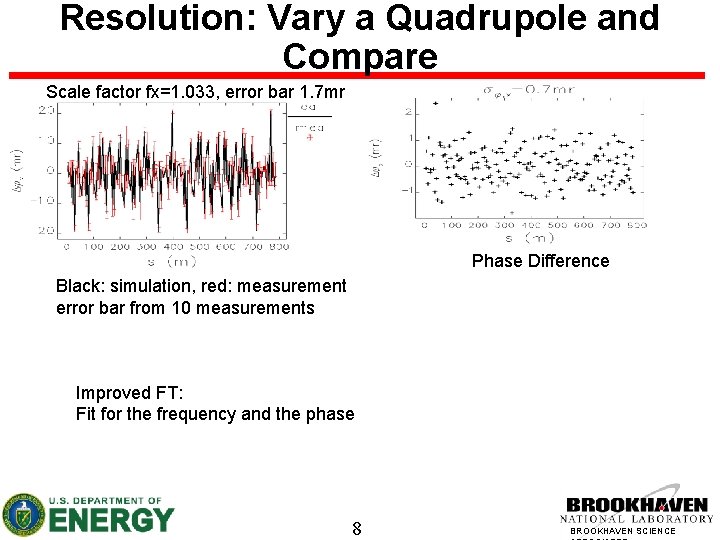
Resolution: Vary a Quadrupole and Compare Scale factor fx=1. 033, error bar 1. 7 mr Phase Difference Black: simulation, red: measurement error bar from 10 measurements Improved FT: Fit for the frequency and the phase 8 BROOKHAVEN SCIENCE

Typical Residue and Comparison with LOCO • The phase error can be corrected to +/- 10 mr • LOCO determines the residual beta-beat is about 1% in both planes. • Possible reasons of the residue: chromatic effect and in-accurate modeling 9 BROOKHAVEN SCIENCE

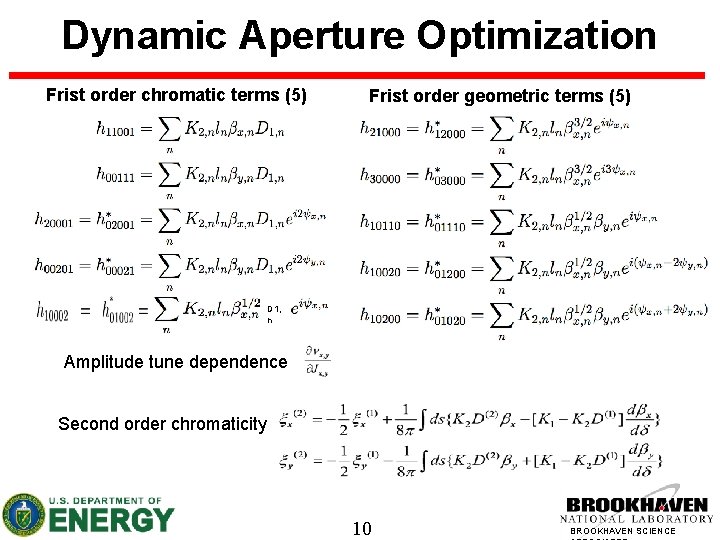
Dynamic Aperture Optimization Frist order chromatic terms (5) Frist order geometric terms (5) D 1, n Amplitude tune dependence Second order chromaticity 10 BROOKHAVEN SCIENCE

Sextupole Correction: the Scheme Linear lattice and coupling must be corrected. 1. Change the orbit by a horizontal corrector, or by tuning the rf frequency 2. Measure the phase change induced by the sextupoles 3. Compare with the model to obtain the phase error 4. Repeat at many correctors and momentum offsets to break degeneracy and improve 5. Measure amplitude dependent de-tuning , and nonlinear chromaticity 6. Assemble the target function and all the response matrices to calculate the correction 11 BROOKHAVEN SCIENCE

Completeness of the Constraints Δψy depends on h 01020, h 10200, h 01110, h 10110, h 01020, h 10020 The off-momentum phase correction corrects the chromatic term: h 11001, h 00111, h 02001, h 20001, h 00021, h 00201, h 10002 Leading order detuning terms: 12 BROOKHAVEN SCIENCE

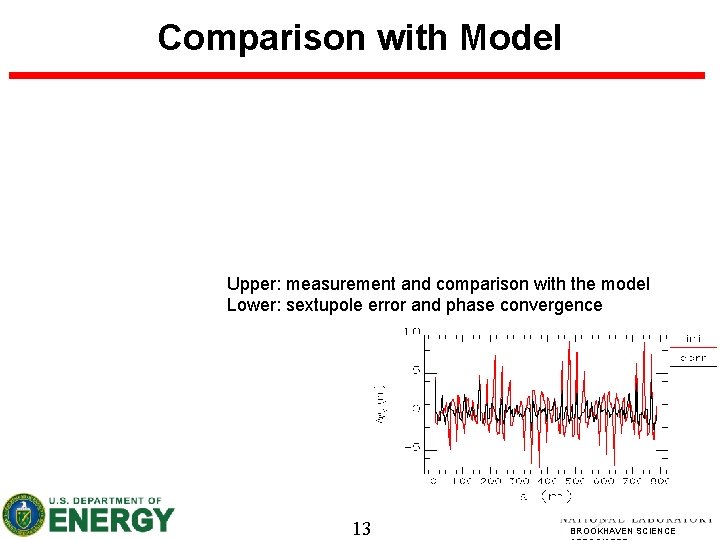
Comparison with Model Upper: measurement and comparison with the model Lower: sextupole error and phase convergence 13 BROOKHAVEN SCIENCE

Correction Results Rms phase error before and after correction 14 Comparison of the dynamic aperture BROOKHAVEN SCIENCE

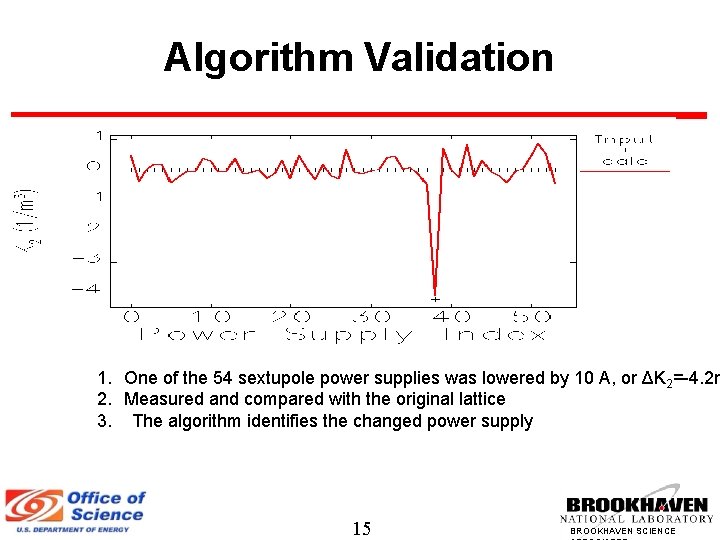
Algorithm Validation 1. One of the 54 sextupole power supplies was lowered by 10 A, or ΔK 2=-4. 2 m 2. Measured and compared with the original lattice 3. The algorithm identifies the changed power supply 15 BROOKHAVEN SCIENCE

Physical Meaning of the Nonlinear Correction • The off-momentum lattice correction has straightforward significance • The lattice correction for the orbit perturbed by a horizontal corrector can be unde 1)The orbit wave is the same as betatron oscillation (with a disruption at the correcto 2)Correcting the phase is equivalent to restoring the transfer matrix for the oscillating undergoes sextupole focusing. 16 BROOKHAVEN SCIENCE

Summary • Phase correction is complementary to LOCO for linear lattice correction; however, phase measurement is fast and independent of BPM calibration • The proposed nonlinear correction approach treats the complete set of nonlinear con • The nonlinear correction method has been verified at NSLS-II. 17 BROOKHAVEN SCIENCE

Acknowledgement W. X. Cheng, J. Choi, Y. Hidaka, B. Podobedov, S. Kramer, V. Smalyuk, T. Shaftan F. Willeke, Xi Yang, L. Yu The coordination group The operations group 18 BROOKHAVEN SCIENCE