Linear and nonLinear Dielectric Response of Periodic Systems

Linear and non-Linear Dielectric Response of Periodic Systems from Quantum Monte Carlo Calculations. Paolo Umari CNR-INFM DEMOCRITOS Theory@Elettra Group Basovizza, Trieste, Italy

In collaboration with: • N. Marzari, Massachusetts Institute of Technology • G. Galli University of California, Davis • A. J. Williamson Lawrence Livermore National Laboratory

Outline Motivations Finite electric fields in QMC with PBCs Results for periodic linear chains of H 2 dimers: polarizability and second hyperpolarizability

Motivations DFT with GGA-LDA not always reliable for dielectric properties:

Motivations… Periodic chains of conjugated polymers, DFT-GGA overestimates: Linear susceptibilities: >~2 times Hyper susceptibilities: > orders of magnitude: importance of electronic correlations

Linear and non-linear optical properties of extended systems We want: • Periodic boundary conditions: real extended solids • Accurate many-body description: conjugate polymers • Scalability: large systems Quantum Monte Carlo

Diffusion - QMC • Wavefunction as stochastic density of walker • The sign of the wavefunction must be known Y • We have errorbars

…. some diffusion-QMC basics • We evolve a trial wave-function into imaginary time: • At large t, we find the exact ground state: • Usually, importance sampling is used, we evolve f in imaginary time:

…need for a new scheme Static dielectric properties are defined as derivative of the system energy with respect to a static electric field for describing extended systems periodic boundary conditions are extremely useful Perturbational approaches can not be (easily) implemented within QMC methods We need: finite electric fields AND periodic boundary conditions

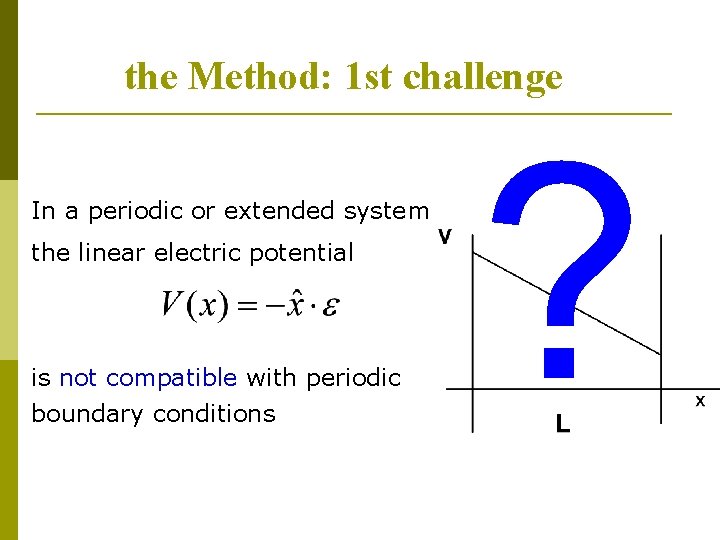
the Method: 1 st challenge In a periodic or extended system the linear electric potential is not compatible with periodic boundary conditions ?

The many-body electric enthalpy • We don’t know how to define a linear potential with PBCs, but the MTP provides a definition for the polarization: • With the N-body operator: • A legendre transform leads to the electric enthalpy functional: PU & A. Pasquarello PRL 89, 157602 (02); I. Souza, J. Iniguez & D. Vanderbilt PRL 89, 117602(‘ 02) R. Resta, PRL 80, 1800 (‘ 98); R. D. King-Smith & D. Vanderbilt PRB 47, 1651 (‘ 93)

2 nd challenge • We want to minimize the electric enthalpy functional • We need an hermitian Hamiltonian • We obtain a Hamiltonian which depends self-consistently upon the wavefunctions: It’s a self-consistent many-body operator !

Iterative maps in the complex plane • For every H(zi) there is a corresponding zi+1 • This define a complex-plane map: f(z) • The solution to the self-consistent scheme and the minimum of the electric enthalpy correspond to the fixed point: • Gives access to the polarization in the presence of the electric field : the solution of our problem

3 rd challenge • Without stochastic error an iterative map can lead to the fixed point: • In QMC, at every zi in the iterative sequence is associated a stochastic error

. . and solution • We can assume that close to the fixed point, the map can be assumed linear: • The average over a sequence of {zi} provides the estimate for the fixed point • The spread of the zi around the fixed point, depends upon the stochastic error:

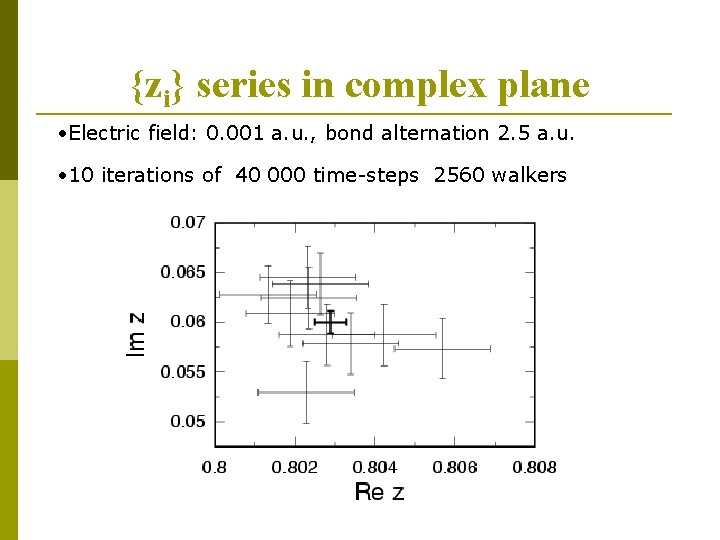
{zi} series in complex plane • Electric field: 0. 001 a. u. , bond alternation 2. 5 a. u. • 10 iterations of 40 000 time-steps 2560 walkers

Implementation: from DFT to QMC First Step (DFT - HF): Hilbert space single Slater determinants: We implemented single-particle electric enthalpy in the quantum-ESPRESSO distribution (publicly available at www. quantum-espresso. org) Second Step (QMC): Wave functions are imported in the CASINO variational and diffusion QMC code, where we coded all the present development (www. tcm. phy. cam. ac. uk/~mdt 26/cqmc. html)

Validation: H atom • We can compare our scheme with a simple sawtooth potential for an isolated system: polarizability of H atom • Isolated H atom in a sawtooth potential: • Same atom in P. B. C. via our new formulation: Exact:

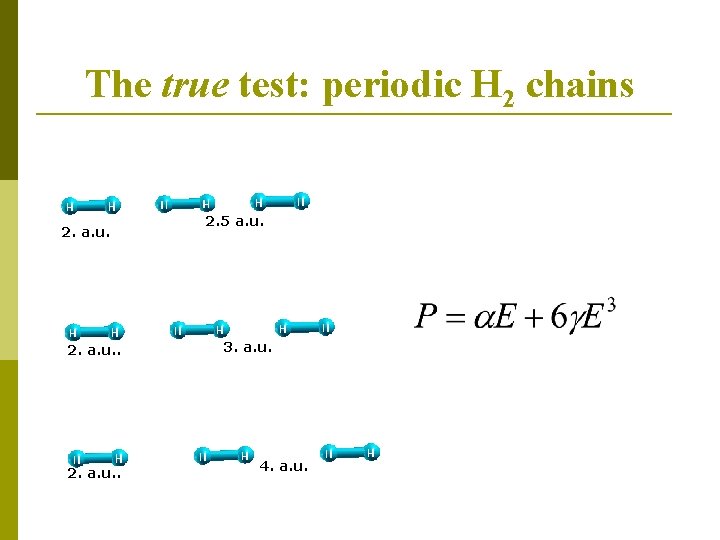
The true test: periodic H 2 chains 2. a. u. . 2. 5 a. u. 3. a. u. 4. a. u.

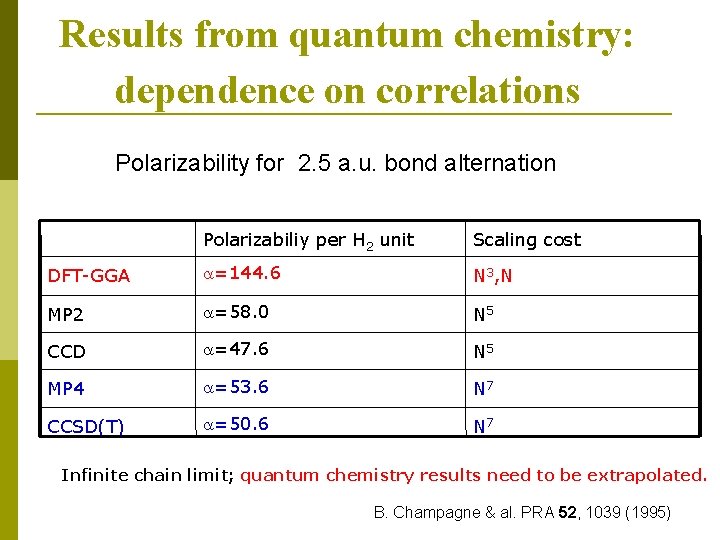
Results from quantum chemistry: dependence on correlations Polarizability for 2. 5 a. u. bond alternation Polarizabiliy per H 2 unit Scaling cost DFT-GGA a=144. 6 N 3, N MP 2 a=58. 0 N 5 CCD a=47. 6 N 5 MP 4 a=53. 6 N 7 CCSD(T) a=50. 6 N 7 Infinite chain limit; quantum chemistry results need to be extrapolated. B. Champagne & al. PRA 52, 1039 (1995)

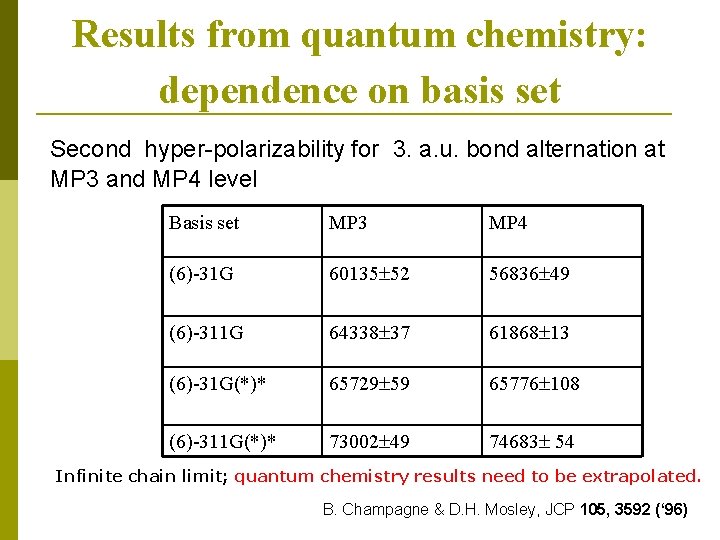
Results from quantum chemistry: dependence on basis set Second hyper-polarizability for 3. a. u. bond alternation at MP 3 and MP 4 level Basis set MP 3 MP 4 (6)-31 G 60135± 52 56836± 49 (6)-311 G 64338± 37 61868± 13 (6)-31 G(*)* 65729± 59 65776± 108 (6)-311 G(*)* 73002± 49 74683± 54 Infinite chain limit; quantum chemistry results need to be extrapolated. B. Champagne & D. H. Mosley, JCP 105, 3592 (‘ 96)

QMC treatment • 2. 5, 3. , 4. a. u. bond alternation • Nodal surface and trial wavefunction from HF • HF wfcs calculated in the presence of electric field

Convergence with respect to supercell size Results from HF, 3. a. u. bond alternation 10 units 20 units QC extrapolations a 27. 8 28. 5 28. 6 g(/1000. ) 57. 1 56. 7 We will consider 10 -H 2 periodic units cells

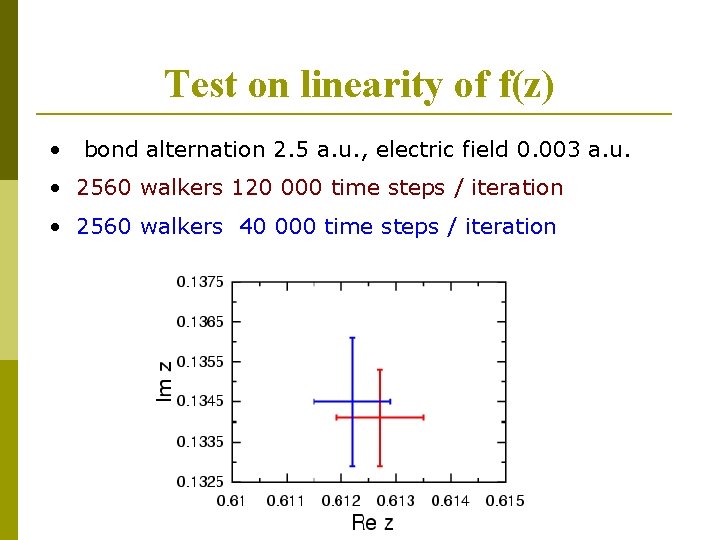
Test on linearity of f(z) • bond alternation 2. 5 a. u. , electric field 0. 003 a. u. • 2560 walkers 120 000 time steps / iteration • 2560 walkers 40 000 time steps / iteration

Diffusion QMC results: 3. a. u. bond alternation • We apply electric fields of: 0. 003 a. u. , 0. 02 a. u. a = 27. 0 +/- 0. 5 a. u. • a=26. 5 a. u. MP 4 From Q. C. extrapolations: • a=25. 7 a. u. CCSD(T) g = 89. 8 +/- 6. 1 a. u. (*103) From Q. C. extrapolations: • g >74. 7 a. u. (*103) MP 4

Diffusion QMC results: 2. 5 a. u. bond alternation • We apply electric fields of: 0. 003 a. u. , 0. 01 a. u. a = 50. 6 +/- 0. 3 a. u. • a=53. 6 a. u. MP 4 From Q. C. extrapolations: • a=50. 6 a. u. CCSD(T) g = 651. 9 +/- 29. 9 a. u. (*103)

Diffusion QMC results: 4. a. u. bond alternation • We apply electric fields of: 0. 01 a. u. , 0. 03 a. u. a = 16. 0 +/- 0. 1 a. u. • a=15. 8 a. u. MP 4 From Q. C. extrapolations: • a=15. 5 a. u. CCSD(T) g = 16. 5 +/- 0. 6 a. u. (*103)

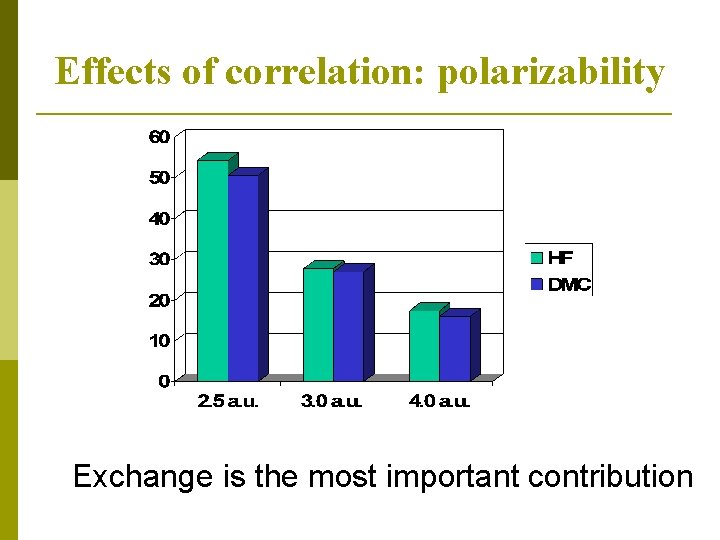
Effects of correlation: polarizability Exchange is the most important contribution

Effects of correlation: 2 nd hyperpolarizability Correlations are important!!

Conclusions • Novel approach for dielectric properties via QMC • Implemented via diffusion QMC • Validated in periodic hydrogen chains: very nice agreement with the best quantum chemistry results • PRL 95, 207602 (‘ 05)

Perspectives… • “Linear scaling” • Testing critical cases • understanding polarization effects in DFT • . .

Acknowledgments • For the QMC CASINO software: M. D. Towler and R. J. Needs, University of Cambridge • For HF applications: S. de Gironcoli, Sissa, Trieste • For money: DARPA-PROM

Importance of nodal surface: from DFT Bond alternation 2. 5 a. u. • For 10 -H 2: a. DMC= 52. 2 +/- 1. 3 a. u. a. GGA= 102. 0 a. u. • For 16 -H 2: a. DMC= 55. 4 +/- 1. 2 a. u. a. GGA= 123. 4 a. u. • For 22 -H 2: a. DMC= 53. 4 +/- 1. 1 a. u. a. GGA= 133. 5 a. u. From nodal surface HF: a. DMC= 50. 6 +/- 0. 3 a. u.

Electronic localization for H 2 periodic chain: • Localization spread: (Resta & Sorella, PRL ’ 99) • For GGA-DFT: • For DMC-QMC:

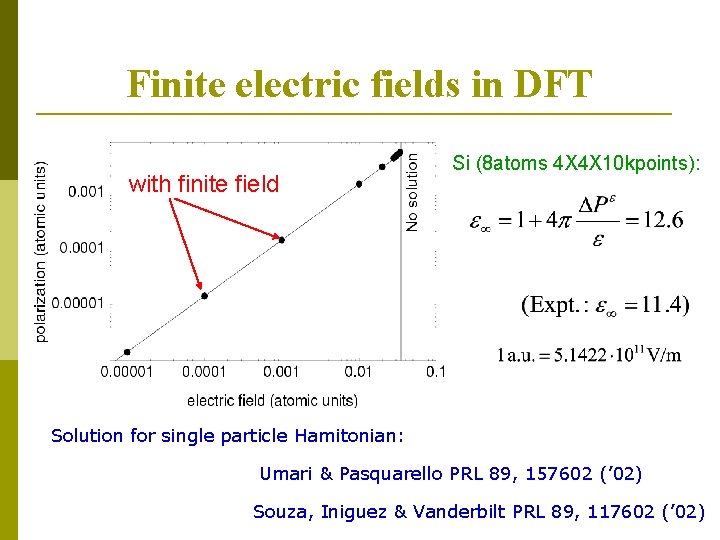
Finite electric fields in DFT with finite field Si (8 atoms 4 X 4 X 10 kpoints): Solution for single particle Hamitonian: Umari & Pasquarello PRL 89, 157602 (’ 02) Souza, Iniguez & Vanderbilt PRL 89, 117602 (’ 02)

…DFT-Molecular Dynamics with electric fields: • Possible applications: • Static Dielectric properties of liquids at finite temperature, (Dubois, PU, Pasquarello, Chem. Phys. Lett. ’ 04) • Dielectric properties of iterfaces (Giustino, PU, Pasquarello, PRL’ 04) • Infrared spectra of large systems • Non-resonant Raman and Hyper-Raman spectra of large systems (Giacomazzi, PU, Pasquarello, PRL’ 05; PU, Pasquarello, PRL’ 05)

Sampling ei. GX in diffusion QMC • ei. GX does not commute with the Hamiltonian: we use forward walking • Observable are samples after a projection time t (Hammond, Lester & Reynolds ’ 94)