Linear Algebraic Equations Gauss Elimination Chapter 9 Credit

~ Linear Algebraic Equations ~ Gauss Elimination Chapter 9 Credit: Prof. Lale Yurttas, Chemical Eng. , Texas A&M University 1 Copyright © 2006 The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

Solving Systems of Equations • A linear equation in n variables: a 1 x 1 + a 2 x 2 + … + anxn = b • For small (n ≤ 3), linear algebra provides several tools to solve such systems of linear equations: – Graphical method – Cramer’s rule – Method of elimination • Nowadays, easy access to computers makes the solution of very large sets of linear algebraic equations possible 2 Copyright © 2006 The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

Determinants and Cramer’s Rule [A] : coefficient matrix D : Determinant of A matrix

Computing the Determinant 4 Copyright © 2006 The Mc. Graw-Hill Companies, Inc. Permission required

Gauss Elimination • Solve Ax = b • Consists of two phases: – Forward elimination – Back substitution Forward Elimination • Forward Elimination reduces Ax = b to an upper triangular system Tx = b’ • Back substitution can then solve Tx = b’ for x Back Substitution 5 Copyright © 2006 The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

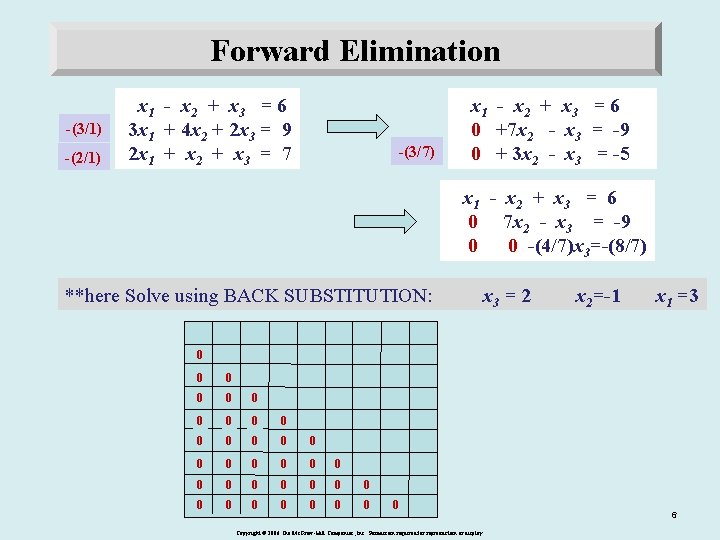
Forward Elimination Gaussian Elimination -(3/1) -(2/1) x 1 - x 2 + x 3 = 6 3 x 1 + 4 x 2 + 2 x 3 = 9 2 x 1 + x 2 + x 3 = 7 -(3/7) x 1 - x 2 + x 3 = 6 0 +7 x 2 - x 3 = -9 0 + 3 x 2 - x 3 = -5 x 1 - x 2 + x 3 = 6 0 7 x 2 - x 3 = -9 0 0 -(4/7)x 3=-(8/7) **here Solve using BACK SUBSTITUTION: x 3 = 2 x 2=-1 x 1 =3 0 0 0 0 0 0 0 0 0 Copyright © 2006 The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display. 6

Back Substitution 1 x 0 x 3 = 2 +1 x 1 – 1 x 2 +4 x 3 = 8 – 2 x 1 – 3 x 2 +1 x 3 = 5 2 x 2 – 3 x 3 = 0 2 x 3 = 4 7 Copyright © 2006 The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

Back Substitution 1 x 0 x 2 = 3 +1 x 1 – 1

Back Substitution 1 x 0 +1 x 1 = 3 x 1 = –

Back Substitution x 0 = 9 1 x 0 = Copyright © 2006 The

Back Substitution (* Pseudocode *) for i n down to 1 do /* calculate xi */ x [ i ] b [ i ] / a [ i, i ] /* substitute x [ i ] in the equations above */ for j 1 to i-1 do b [ j ] x [ i ] × a [ j, i ] endfor Time Complexity? O(n 2) 11 Copyright © 2006 The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

Forward Elimination Gaussian Elimination 12 Copyright © 2006 The Mc. Graw-Hill Companies, Inc. Permission

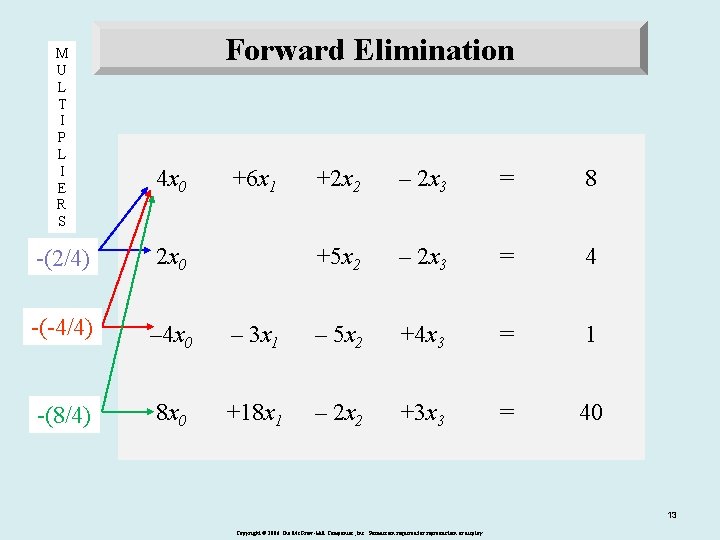
M U L T I P L I E R S Forward Elimination 4 x 0 +6 x 1 +2 x 2 – 2 x 3 = 8 +5 x 2 – 2 x 3 = 4 -(2/4) 2 x 0 -(-4/4) – 4 x 0 – 3 x 1 – 5 x 2 +4 x 3 = 1 -(8/4) 8 x 0 +18 x 1 – 2 x 2 +3 x 3 = 40 13 Copyright © 2006 The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

Forward Elimination M U L T I P L I E R S 4 x 0 +6 x 1 +2 x 2 – 2 x 3 = 8 – 3 x 1 +4 x 2 – 1 x 3 = 0 -(3/-3) +3 x 1 – 3 x 2 +2 x 3 = 9 -(6/-3) +6 x 1 – 6 x 2 +7 x 3 = 24 14 Copyright © 2006 The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

Forward Elimination 4 x 0 M U L T I P L I E R ? ? +6 x 1 +2 x 2 – 2 x 3 = 8 – 3 x 1 +4 x 2 – 1 x 3 = 0 1 x 2 +1 x 3 = 9 2 x 2 +5 x 3 = 24 15 Copyright © 2006 The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

Forward Elimination 4 x 0 +6 x 1 +2 x 2 – 2 x 3 = 8 – 3 x 1 +4 x 2 – 1 x 3 = 0 1 x 2 +1 x 3 = 9 3 x 3 = 6 16 Copyright © 2006 The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

Operation count in Forward Elimination Gaussian Elimination b 11 2 n 0 0 0 0 2 n 0 0 0 0 0 0 0 b 22 b 33 b 44 b 55 b 66 b 77 b 66 0 b 66 TOTAL 1 st column: 2 n(n-1) 2 n 2 2(n-1)2 2(n-2)2 ……. 17 Copyright © 2006 The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

Pitfalls of Elimination Methods Division by zero It is possible that during both elimination and back-substitution phases a division by zero can occur. For example: 2 x 2 + 3 x 3 = 8 4 x 1 + 6 x 2 + 7 x 3 = -3 2 x 1 + x 2 + 6 x 3 = 5 Solution: A= 0 4 2 2 6 1 3 7 6 pivoting (to be discussed later) 18 Copyright © 2006 The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

Pitfalls (cont. ) Round-off errors • Because computers carry only a limited number of significant figures, round -off errors will occur and they will propagate from one iteration to the next. • This problem is especially important when large numbers of equations (100 or more) are to be solved. • Always use double-precision numbers/arithmetic. It is slow but needed for correctness! • It is also a good idea to substitute your results back into the original equations and check whether a substantial error has occurred. 19 Copyright © 2006 The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

Pitfalls (cont. ) ill-conditioned systems - small changes in coefficients result in large changes in the solution. Alternatively, a wide range of answers can approximately satisfy the equations. (Well-conditioned systems – small changes in coefficients result in small changes in the solution) Problem: Since round off errors can induce small changes in the coefficients, these changes can lead to large solution errors in ill-conditioned systems. Example: x 1 + 2 x 2 = 10 1. 1 x 1 + 2 x 2 = 10. 4 x 1 + 2 x 2 = 10 1. 05 x 1 + 2 x 2 = 10. 4 Copyright © 2006 The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

ill-conditioned systems (cont. ) – • Surprisingly, substitution of the erroneous values, x 1=8 and x 2=1, into the original equation will not reveal their incorrect nature clearly: x 1 + 2 x 2 = 10 8+2(1) = 10 (the same!) 1. 1 x 1 + 2 x 2 = 10. 4 1. 1(8)+2(1)=10. 8 (close!) IMPORTANT OBSERVATION: An ill-conditioned system is one with a determinant close to zero • If determinant D=0 then there are infinitely many solutions singular system • Scaling (multiplying the coefficients with the same value) does not change the equations but changes the value of the determinant in a significant way. However, it does not change the ill-conditioned state of the equations! DANGER! It may hide the fact that the system is ill-conditioned!! How can we find out whether a system is ill-conditioned or not? Not easy! Luckily, most engineering systems yield well-conditioned results! • One way to find out: change the coefficients slightly and recompute & compare Copyright © 2006 The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

COMPUTING THE DETERMINANT OF A MATRIX USING GAUSSIAN ELIMINATION The determinant of a matrix can be found using Gaussian elimination. Here are the rules that apply: • • Interchanging two rows changes the sign of the determinant. Multiplying a row by a scalar multiplies the determinant by that scalar. Replacing any row by the sum of that row and the multiple of any other row does NOT change the determinant. The determinant of a triangular matrix (upper or lower triangular) is the product of the diagonal elements. i. e. D=t 11 t 22 t 33 22 Copyright © 2006 The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

Techniques for Improving Solutions • Use of more significant figures – double precision arithmetic • Pivoting If a pivot element is zero, normalization step leads to division by zero. The same problem may arise, when the pivot element is close to zero. Problem can be avoided: – Partial pivoting Switching the rows below so that the largest element is the pivot element. **here* Go over the solution in: CHAP 9 e-Problem-11. doc – Complete pivoting • Searching for the largest element in all rows and columns then switching. • This is rarely used because switching columns changes the order of x’s and adds significant complexity and overhead costly • Scaling – used to reduce the round-off errors and improve accuracy Copyright © 2006 The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

Gauss-Jordan Elimination a 11 0 0 0 0 b 11 0 x 22 0 0 0 0 b 22 0 0 x 33 0 0 0 b 33 0 0 0 x 44 0 0 0 b 44 0 0 x 55 0 0 b 55 0 0 0 x 66 0 0 0 b 66 0 0 0 x 77 0 0 b 77 0 0 0 0 x 88 0 b 88 0 0 0 0 x 99 b 99 24 Copyright © 2006 The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

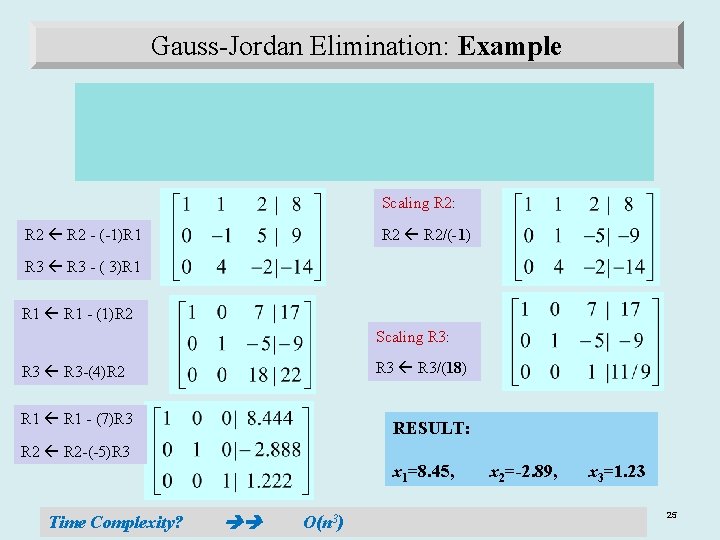
Gauss-Jordan Elimination: Example Scaling R 2: R 2/(-1) R 2 - (-1)R 1 R 3 - ( 3)R 1 - (1)R 2 Scaling R 3: R 3/(18) R 3 -(4)R 2 R 1 - (7)R 3 RESULT: R 2 -(-5)R 3 x 1=8. 45, Time Complexity? O(n 3) Copyright © 2006 The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display. x 2=-2. 89, x 3=1. 23 25

Systems Equations Systemsof of Nonlinear Equations • Locate the roots of a set of simultaneous nonlinear equations: 26 Copyright © 2006 The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

• First-order Taylor series expansion of a function with more than one variable: • The root of the equation occurs at the value of x 1 and x 2 where f 1(i+1) =0 and f 2(i+1) =0 Rearrange to solve for x 1(i+1) and x 2(i+1) • Since x 1(i), x 2(i), f 1(i), and f 2(i) are all known at the ith iteration, this represents a set of two linear equations with two unknowns, x 1(i+1) and x 2(i+1) • You may use several techniques to solve these equations Copyright © 2006 The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

General Representation for the solution of Nonlinear Systems of Equations Jacobian Matrix Solve this set of linear equations at each iteration: {X}(i+1) values are found by solving this system of linear equations. These iterations will continue until the convergence is reached; which will happen when the approximate relative error (defined on the vector of values) falls below the desired error tolerance Copyright © 2006 The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display. εtol 28

Solution of Nonlinear Systems of Equations Solve this set of linear equations at each iteration: Rearrange: 29 Copyright © 2006 The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

Notes on the solution of Nonlinear Systems of Equations n non-linear equations n unknowns to be solved: Jacobian Matrix: • Need to solve this set of Linear Equations in each and every iterative solution of the original Non-Linear system of equations. • For n unknowns, the size of the Jacobian matrix is n 2 and the time it takes to solve the linear system of equations (one iteration of the non-linear system) is proportional to O(n 3) • There is no guarantee for the convergence of the non-linear system. There may also be slow convergence. • In summary, finding the solution set for the Non-Linear system of equations is an extremely compute-intensive task. 30 Copyright © 2006 The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.