Linear Algebraic Equations and Matrices In previous units

Linear Algebraic Equations and Matrices In previous units, we determined the value x satisfying a single equation f(x) = 0. Now we determine the values x 1, x 2, . . . , xn that simultaneously satisfy a set of equations

A Linear System Means What? 2

You Got A Problem } “Suppose that three jumpers are connected by bungee cords. Subfigure (a) shows them being held in place vertically so that each cord is fully extended but unstretched. We define three distances, x 1, x 2, and x 3, as measured downward from each of their unstretched positions. After they are released, gravity takes hold and jumpers eventually come to equilibrium positions (subfigure (b)). } How to compute the displacement of each of the three jumpers. ” 3

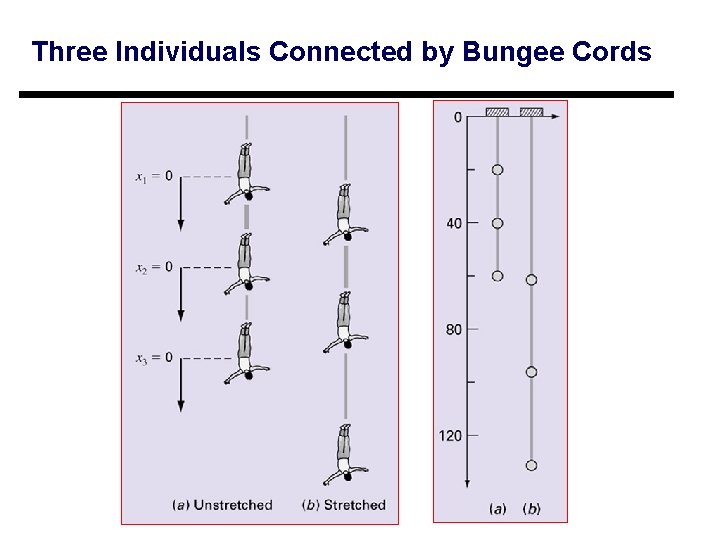
Three Individuals Connected by Bungee Cords

Free-Body Diagrams } Newton’s second law Rearrange equations [K] {x} = {b} 5

Newton’s Second Law – Equation of Motion } Mass-spring system (similar to bungee jumpers) } Kirchhoff’s current and voltage rules Resistor circuits 6

Linear Algebraic Equations: Example (1/2) } Diet problem } Amounts of protein, carbohydrate and fat in nonfat milk, soy flour and whey are given by the following table: } Find the amounts of nonfat milk, soy flour and whey that give a product containing 33 g protein, 45 g carbohydrate and 3 g fat 7

Linear Algebraic Equations: Example (2/2) } Diet problem } Find the amounts of nonfat milk, soy flour and whey that give a product containing 33 g protein, 45 g carbohydrate and 3 g fat } Take a combination of x 1, x 2, x 3 in 100 g of nonfat milk, soy flour, and whey, respectively, in a day } Total amounts of protein, carbohydrate and fat in a day: - protein: 36 x 1 + 51 x 2 + 13 x 3 - carbohydrate: 52 x 1 + 34 x 2 + 74 x 3 - fat: 7 x 2 + 1. 1 x 3 } Now choose a combination of x 1, x 2, x 3 in 100 g such that 8

Linear Algebraic Equations } Solved a single equation } Now consider more than one variable and more than one equation

Linear Systems } Linear equations and constant coefficients } aij and bi are constants 10

Mathematical Background } Write a system of equations in matrix-vector form 11

Solving Systems of Linear Equations } Two ways to solve systems of linear algebraic equations [A]{x}={b} } Left-division x = Ab } Matrix inversion x = inv(A)*b } Matrix inversion only works for square, nonsingular systems } Less efficient than left-division 12

Vector Multiplication, Division } Vector multiplication >> x=[1 2 3]; >> pi*x %scalar multiplication ans = 3. 1416 6. 2832 9. 4248 >> x=[1 2 3]; >> y=[4 5 6]; >> x. *y %vector operation ans = 4 10 18 } Vector division is not defined in algebra but represented in MATLAB by x. /y means x. y means >> x=[1 2 3]; >> y=[4 5 6]; >> x. /y %vector operation ans = 0. 2500 0. 4000 0. 5000 13

Matrix Notations Column 4 (second index) Row 3 (first index) 14

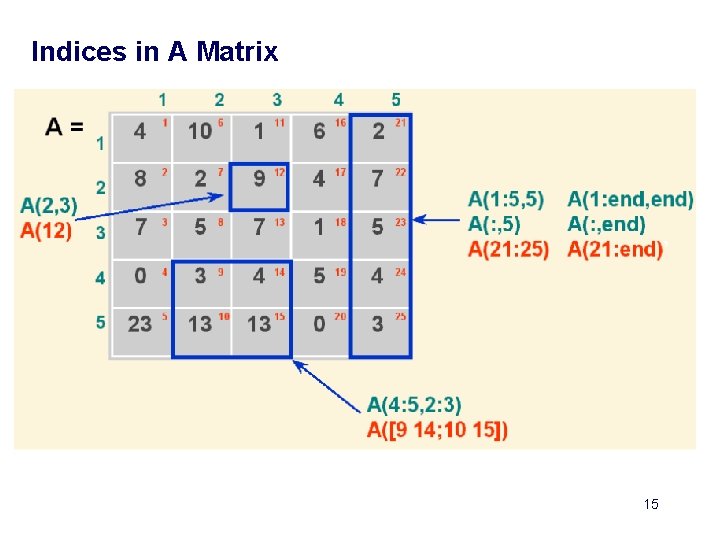
Indices in A Matrix 15

Scalars, Vectors, Matrices } MATLAB treats variables as “matrices” } Matrix (m n) - a set of numbers arranged in rows (m) and columns (n) } Scalar: 1 1 matrix } Row vector: 1 n matrix } Column vector: m 1 matrix 16

Matrix Operations } Transpose } In MATLAB, transpose is A } Trace is sum of diagonal elements } In MATLAB, trace(A) 17

Matrix Transpose 18

Special Matrices } Symmetric matrices aij = aji T [A] = [A] 19

Special Matrices } Diagonal matrix } Identity matrix [A][I] = [I][A] = [A] 20

Special Matrices } Banded matrix – all elements are zero, with the exception of a band centered on the main diagonal Tridiagonal – three non-zero bands 21

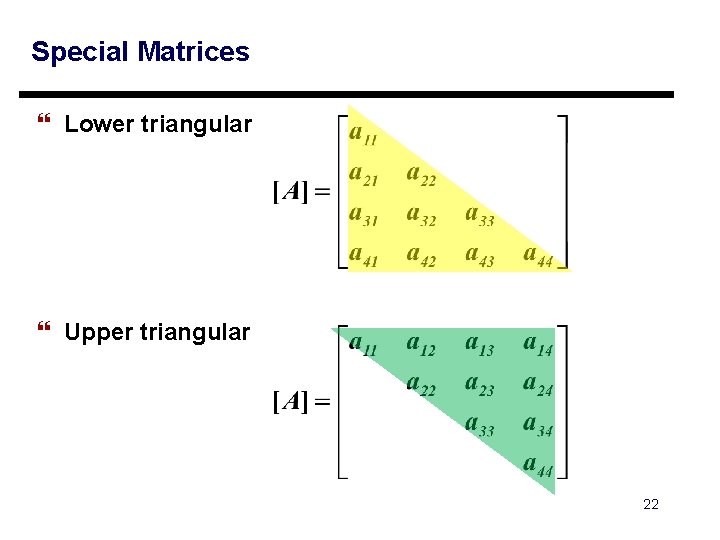
Special Matrices } Lower triangular } Upper triangular 22

Matrix Operations } Matrix identity [A] = [B] if and only if aij = bij for all i and j } Matrix addition and subtraction [C] = [A] + [B] Cij = Aij + Bij [C] = [A] [B] Cij = Aij Bij } Commutative [A] + [B] = [B] + [A] } Associative ( [A] + [B] ) + [C] = [A] + ( [B] + [C] ) ( [A] + [B] ) [C] = [A] + ( [B] [C] ) ( [A] [B] ) + [C] = [A] + ( [B] + [C] )

Multiplication of Matrix by a Scalar g=5

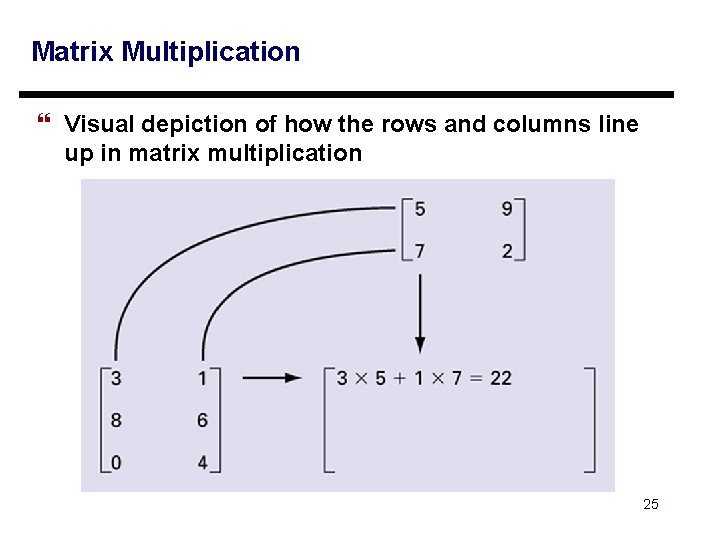
Matrix Multiplication } Visual depiction of how the rows and columns line up in matrix multiplication 25

Matrix Multiplication [A]*[B] [B]*[A]

Matrix Multiplication } Matrix multiplication can be performed only if the inner dimensions are equal 27

Matrix Multiplication } Interior dimensions must be equal } For a vector } We will be using square matrices 28

Matrix Multiplications } MATLAB performs matrix multiplication automatically A*B = C } Note: no period ‘. ’ (not element-by-element operation) } For vectors A*x = b } Associative ( [A] [B] ) [C] = [A] ( [B] [C] ) } Distributive [A] ( [B] + [C] ) = [A] [B] + [A] [C] ([A] + [B] ) [C] = [A] [C] + [B] [C] } Not generally commutative [A] [B] [A] 29

Matrix Inverse } Matrix division is undefined } However, there is a matrix inverse for non-singular square matrices [A]-1 [A] = [A]-1 = [I] } Multiplication of a matrix by the inverse is analogous to division 30

Augmented Matrix Can be used to find the inverse of a matrix } Whatever you do to left-hand-side, do to the righthand side (useful when solving system of equations) 31

Augmented Matrix

MATLAB Matrix Manipulations >> A = [1 5 3 -4; 2 5 6 -1; 3 4 -2 5; -1 3 2 6] A = 1 5 3 -4 2 5 6 -1 3 4 -2 5 -1 3 2 6 >> A' Create a matrix Matrix transpose ans = 1 2 3 -1 5 5 4 3 3 6 -2 2 -4 -1 5 6

MATLAB Matrix Manipulations } Matrix concatenation >> x = [5 1 >> C = A + B -2 3]; >> y = [2 -1 4 2]; 6 6 1 -1 >> z = [3 -2 1 -5]; 4 4 10 1 >> B = [x; y; x; z] 8 5 -4 8 B = 2 1 3 1 C = 5 1 -2 3 >> C = C – B 2 -1 4 2 C = 5 1 -2 3 1 5 3 -4 3 -2 1 -5 2 5 6 -1 3 4 -2 5 -1 3 2 6 ( = A)

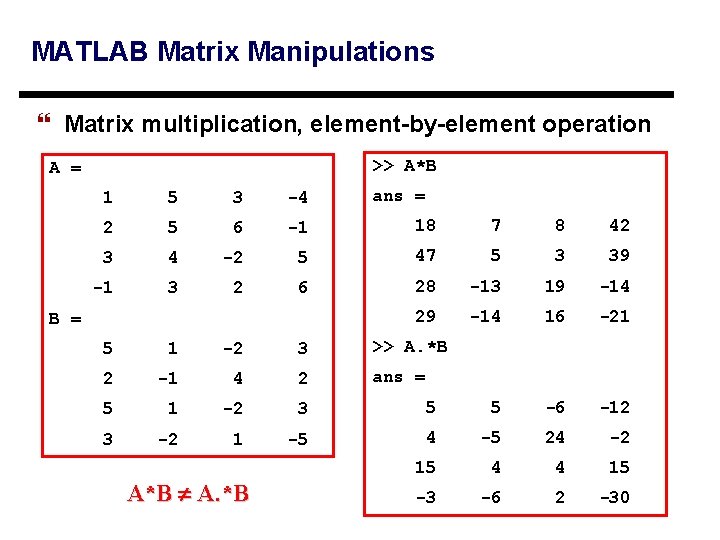
MATLAB Matrix Manipulations } Matrix multiplication, element-by-element operation >> A*B A = ans = 1 5 3 -4 2 5 6 -1 18 7 8 42 3 4 -2 5 47 5 3 39 -1 3 2 6 28 -13 19 -14 29 -14 16 -21 B = 5 1 -2 3 >> A. *B 2 -1 4 2 ans = 5 1 -2 3 5 5 -6 -12 3 -2 1 -5 4 -5 24 -2 15 4 4 15 -3 -6 2 -30 A*B A. *B

MATLAB Matrix Manipulations A = >> D = [2 4 3 1; 3 -5 1 2; 1 -1 3 2] 1 5 3 -4 2 5 6 -1 2 4 3 1 3 4 -2 5 3 -5 1 2 -1 3 2 6 1 -1 3 2 D = >> A*D ? ? ? Error using ==> * Inner dimension must agree Inner matrix dimensions must agree. A*D D*A ans = >> D*A 18 45 26 9 -6 0 -19 10 6 18 -5 24

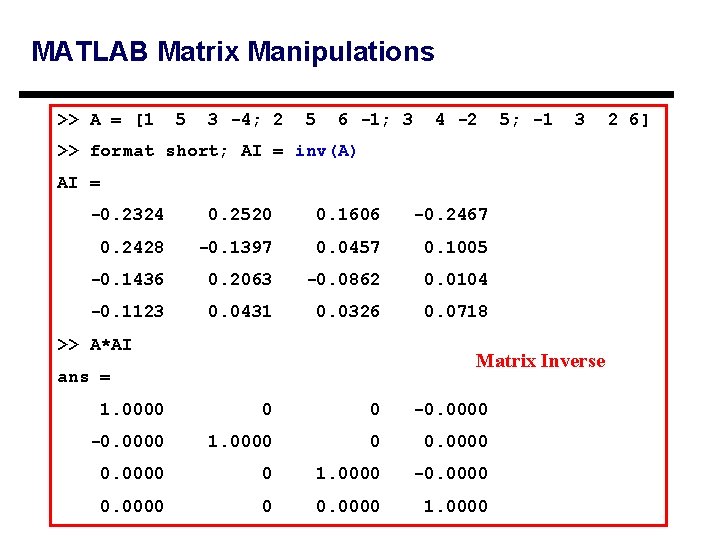
MATLAB Matrix Manipulations >> A = [1 5 3 -4; 2 5 6 -1; 3 4 -2 5; -1 3 >> format short; AI = inv(A) AI = -0. 2324 0. 2520 0. 1606 -0. 2467 0. 2428 -0. 1397 0. 0457 0. 1005 -0. 1436 0. 2063 -0. 0862 0. 0104 -0. 1123 0. 0431 0. 0326 0. 0718 >> A*AI Matrix Inverse ans = 1. 0000 0 0 -0. 0000 1. 0000 0 0. 0000 0 1. 0000 -0. 0000 0 0. 0000 1. 0000 2 6]

MATLAB Matrix Manipulations >> A = [1 5 3 -4; 2 5 6 -1; 3 4 -2 5; -1 3 2 6] >> I = eye(4) I = 1 0 0 0 0 1 >> Aug = [A I] %matrix augmentation Aug = 1 5 3 -4 1 0 0 0 2 5 6 -1 0 0 3 4 -2 5 0 0 1 0 -1 3 2 6 0 0 0 1 >> [n, m] = size(Aug) n = 4 m = 8

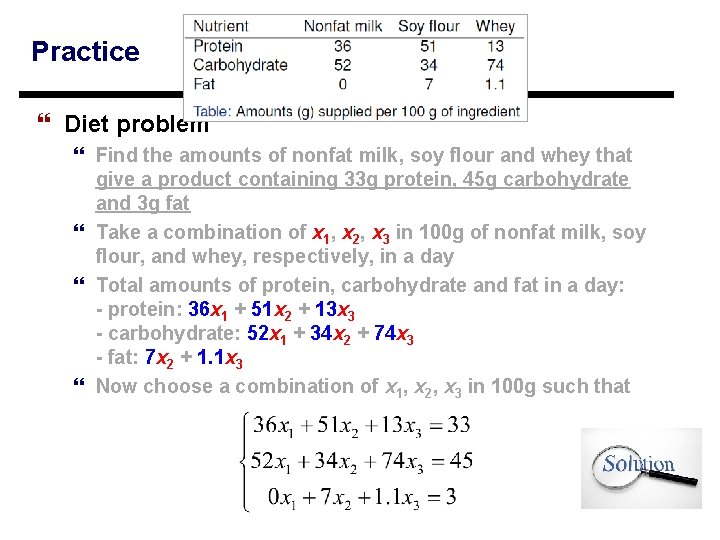
Practice } Diet problem } Find the amounts of nonfat milk, soy flour and whey that give a product containing 33 g protein, 45 g carbohydrate and 3 g fat } Take a combination of x 1, x 2, x 3 in 100 g of nonfat milk, soy flour, and whey, respectively, in a day } Total amounts of protein, carbohydrate and fat in a day: - protein: 36 x 1 + 51 x 2 + 13 x 3 - carbohydrate: 52 x 1 + 34 x 2 + 74 x 3 - fat: 7 x 2 + 1. 1 x 3 } Now choose a combination of x 1, x 2, x 3 in 100 g such that 39

Bungee Jumpers Jumper Mass (kg) Spring constant (N/m) Unstretched cord length (m) Top (1) 60 50 20 Middle (2) 70 100 20 Bottom (3) 80 50 20 [K] {x} = {b}

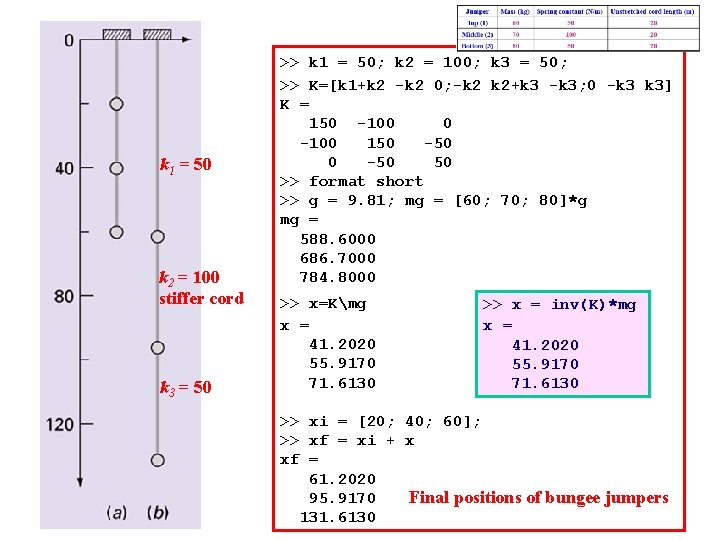
k 1 = 50 k 2 = 100 stiffer cord k 3 = 50 >> k 1 = 50; k 2 = 100; k 3 = 50; >> K=[k 1+k 2 -k 2 0; -k 2 k 2+k 3 -k 3; 0 -k 3 k 3] K = 150 -100 150 -50 50 >> format short >> g = 9. 81; mg = [60; 70; 80]*g mg = 588. 6000 686. 7000 784. 8000 >> x=Kmg x = 41. 2020 55. 9170 71. 6130 >> x = inv(K)*mg x = 41. 2020 55. 9170 71. 6130 >> xi = [20; 40; 60]; >> xf = xi + x xf = 61. 2020 95. 9170 Final positions of bungee jumpers 131. 6130

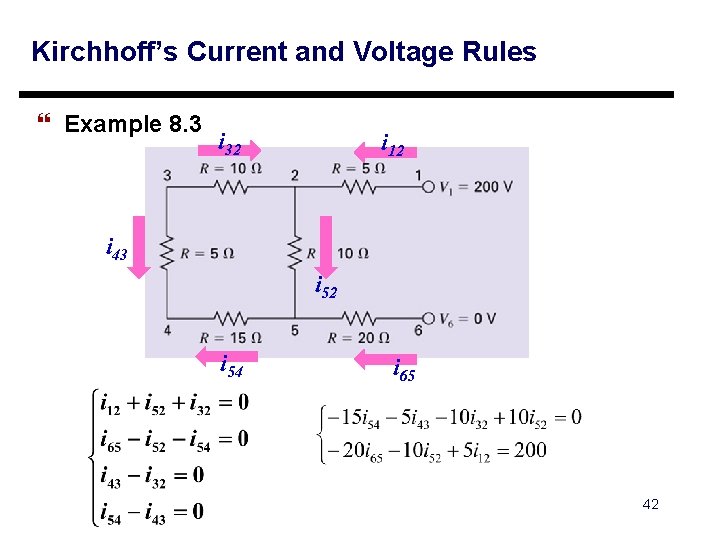
Kirchhoff’s Current and Voltage Rules } Example 8. 3 i 32 i 12 i 43 i 52 i 54 i 65 42

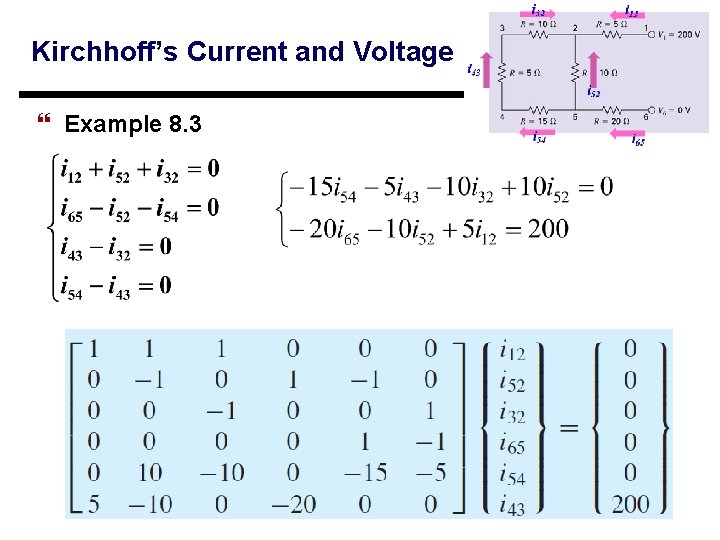
Kirchhoff’s Current and Voltage Rules } Example 8. 3 43

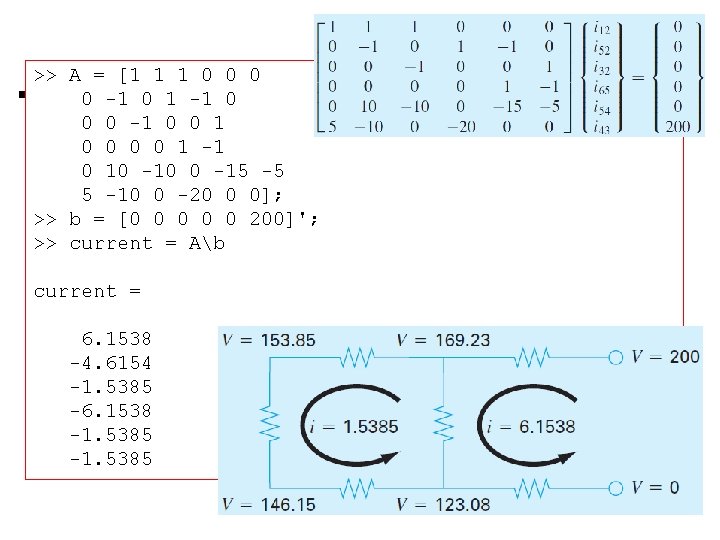
>> A = [1 1 1 0 0 -1 0 1 -1 0 0 0 0 1 -1 0 10 -10 0 -15 -5 5 -10 0 -20 0 0]; >> b = [0 0 0 200]'; >> current = Ab current = 6. 1538 -4. 6154 -1. 5385 -6. 1538 -1. 5385