LINEAR ALGEBRA Matrices Matrix Operations and Properties Determinants

LINEAR ALGEBRA Matrices Matrix Operations and Properties Determinants

MATRICES

MATRICES

MATRICES The size of a matrix is described in terms of the number of rows (horizontal lines) and columns (vertical lines) it contains. For example, the first matrix in Example 1 has three rows and two columns, so its size is 3 by 2 (written 3 × 2). In a size description, the first number always denotes the number of rows, and the second denotes the number of columns.

MATRICES

MATRICES

MATRICES

MATRICES

CLASSIFICATION OF MATRICES

CLASSIFICATION OF MATRICES

CLASSIFICATION OF MATRICES

CLASSIFICATION OF MATRICES

CLASSIFICATION OF MATRICES

TRANSPOSE OF A MATRIX

CLASSIFICATION OF MATRICES

MATRIX OPERATIONS AND PROPERTIES

DEFINITION

EQUALITY OF MATRICES

DEFINITION

ADDITION AND SUBTRACTION

DEFINITION

SCALAR MULTIPLES

DEFINITION

DEFINITION
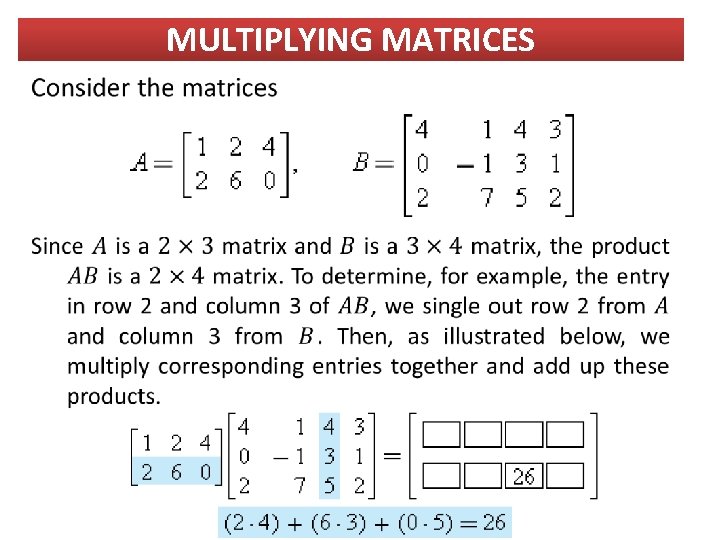
MULTIPLYING MATRICES
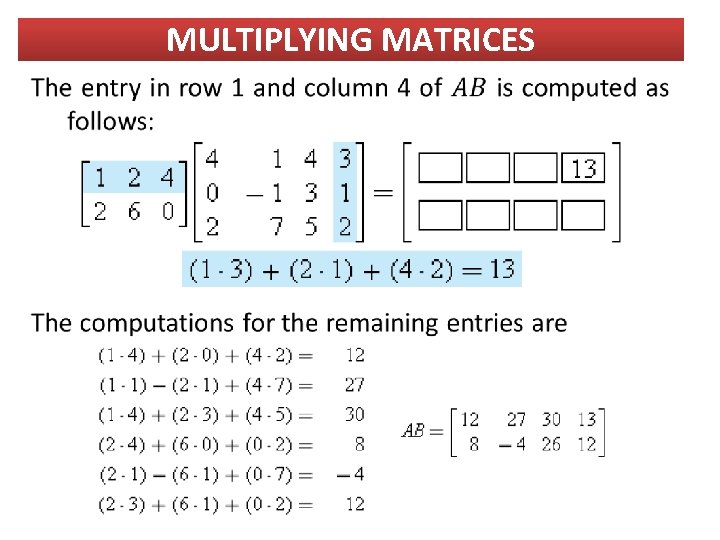
MULTIPLYING MATRICES

MULTIPLYING MATRICES

Determining Whether a Product is Defined

Determining Whether a Product is Defined

DETERMINANTS

PERMUTATION

PERMUTATION

INVERSION

INVERSION Solution: a) (3, 1, 4, 2) We will start at the left most number and count the number of numbers to the right that are smaller. We then move to the second number and do the same thing. We continue in this manner until we get to the end. The total number of inversions are then the sum of all these. (3, 1, 4, 2) 2 inversions (3, 1, 4, 2) 0 inversions (3, 1, 4, 2) 1 inversion The permutation (3, 1, 4, 2) has a total of 3 inversions.

INVERSION b) (1, 2, 4, 3) 0 + 1 =1 inversion c) (4, 3, 2, 1) 3 + 2 + 1 = 6 inversions d) (1, 2, 3, 4, 5) No inversions e) (2, 5, 4, 1, 3) 1 + 3 + 2 + 0 = 6 inversions

PERMUTATION A permutation is called even if the number of inversions is even and odd if the number of inversions is odd. Example 4: Classify as even or odd all the permutations of the following lists. a) {1, 2} b) {1, 2, 3} Solution: a)
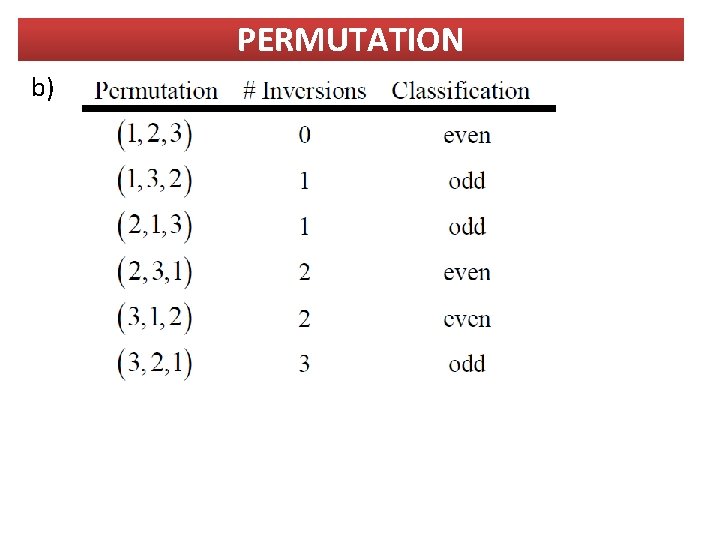
PERMUTATION b)

ELEMENTARY PRODUCT

ELEMENTARY PRODUCT

ELEMENTARY PRODUCT

ELEMENTARY PRODUCT

SIGNED ELEMENTARY PRODUCT
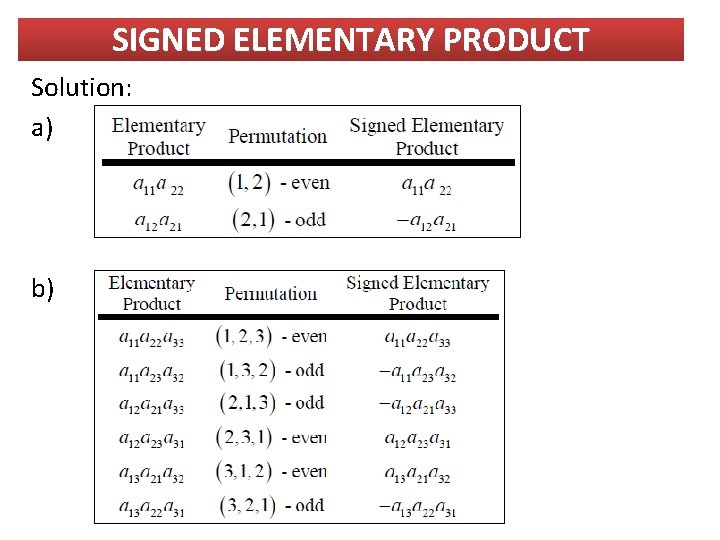
SIGNED ELEMENTARY PRODUCT Solution: a) b)

DEFINITION 1

DETERMINANT

METHODS OF FINDING A SOLUTION

METHODS OF FINDING A SOLUTION

METHODS OF FINDING A SOLUTION

EXERCISES

EXERCISES II. Use Cramer’s rule to solve the ff. linear system x–y+z=4 2 x + y + z = 7 – x – 2 y + 2 z = – 1
- Slides: 50