Lineaire Verbanden Hoofdstuk 3 Een grafiek tekenen Y

Lineaire Verbanden Hoofdstuk 3

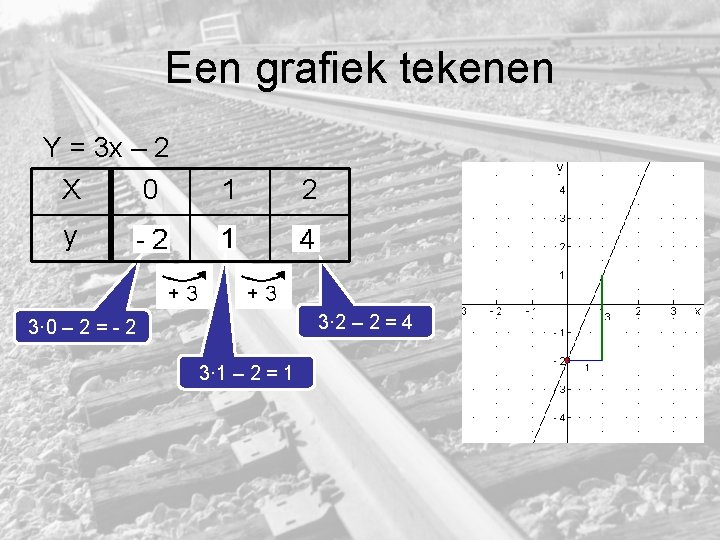
Een grafiek tekenen Y = 3 x – 2 X 0 1 2 y 3· 2 – 2 = 4 3· 0 – 2 = - 2 3· 1 – 2 = 1

Paragraaf 1 • Een lineair (liniaal) verband is altijd een rechte lijn. • De algemene formule van een lineair verband is y = ax + b – Als je één stap opzij gaat, ga je a omhoog/omlaag. – De y-as wordt gesneden in het punt (0, b)

y = 2 x + 3 • De standaardformule was: y = ax + b • y = 2 x + 3 a=2 b=3 • Dus deze grafiek “begint” bij (0, 3) • En als ik één stap opzij ga, ga ik 2 omhoog.

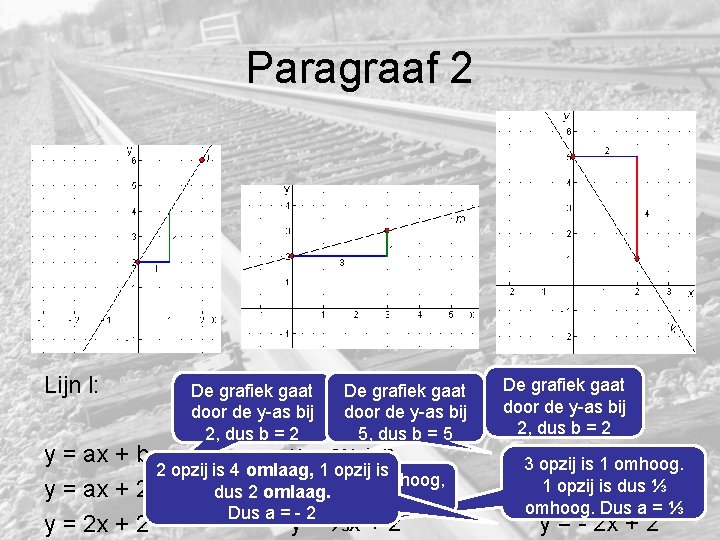
Paragraaf 2 Lijn l: Lijn m: De grafiek gaat door de y-as bij 2, dus b = 2 De grafiek gaat door de y-as bij 5, dus b = 5 y = ax + b 2 opzij is 4 omlaag, 1 opzij is 1 opzij, is 2 omhoog, y = dus ax a+=22 y = ax + 2 dus 2 omlaag. Dus a = - 2 y = ⅓x + 2 y = 2 x + 2 De Lijngrafiek k: gaat door de y-as bij 2, dus b = 2 y = ax b 3 opzij is 1 + omhoog. y 1 opzij = axis+dus 5⅓ omhoog. Dus a = ⅓ y = - 2 x + 2

Hellingsgetal • Y=ax + b • B, is makkelijk… Hier “begint” de grafiek (snijdt de grafiek de y-as) • a is moeilijker, want dat kan ik niet altijd aflezen!

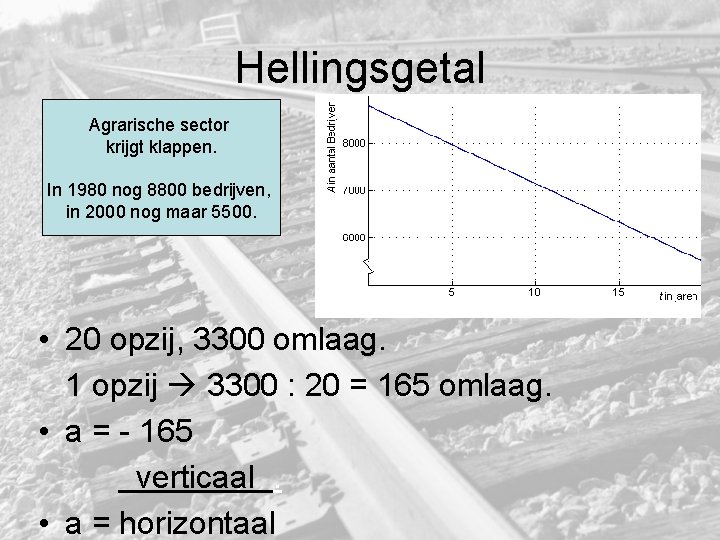
Hellingsgetal Agrarische sector krijgt klappen. In 1980 nog 8800 bedrijven, in 2000 nog maar 5500. • 20 opzij, 3300 omlaag. 1 opzij 3300 : 20 = 165 omlaag. • a = - 165 verticaal. • a = horizontaal