Line of Best Fit LG I can sketch

Line of Best Fit LG: I can sketch a line of best fit, determine an equation for the line, and use this equation to make predictions LG: I can assess the reliability of a linear model

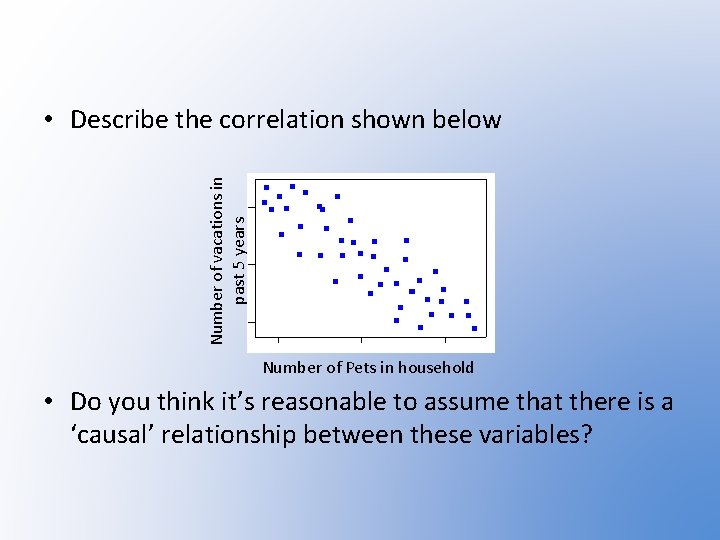
Number of vacations in past 5 years • Describe the correlation shown below Number of Pets in household • Do you think it’s reasonable to assume that there is a ‘causal’ relationship between these variables?

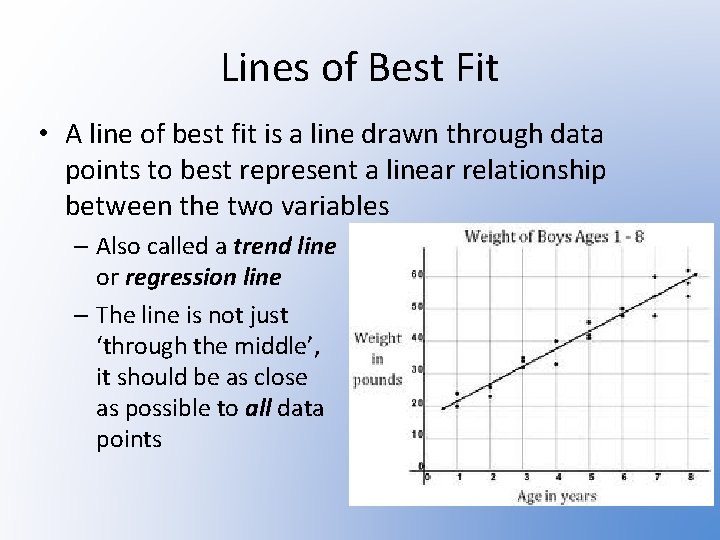
Lines of Best Fit • A line of best fit is a line drawn through data points to best represent a linear relationship between the two variables – Also called a trend line or regression line – The line is not just ‘through the middle’, it should be as close as possible to all data points

Outliers • Any point that lies far away from the main cluster of points is an outlier – May be caused by inaccurate measurements, or may be unusual but still valid – The line of best fit should reflect all valid data points, including outliers

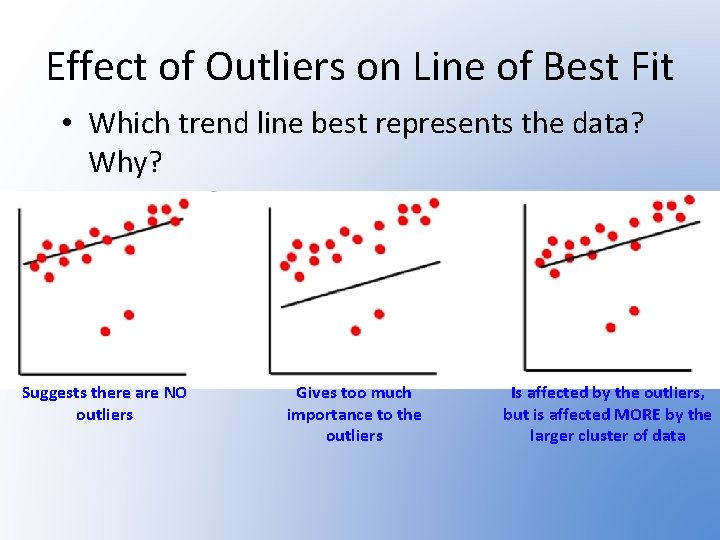
Effect of Outliers on Line of Best Fit • Which trend line best represents the data? Why? Suggests there are NO outliers Gives too much importance to the outliers Is affected by the outliers, but is affected MORE by the larger cluster of data

Recall: Find the equation of this line y = mx + b • STEP 1: Choose 2 points on the line • STEP 2: Find slope • STEP 3: Find y-intercept • STEP 4: state equation

Using a Line of Best Fit to Make Predictions • Interpolation – Predictions WITHIN data point • Extrapolation – Predictions BEYOND data points

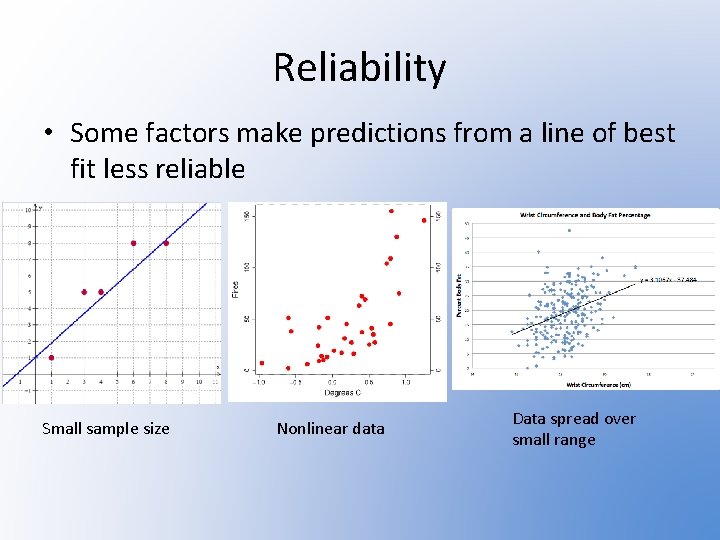
Reliability • Some factors make predictions from a line of best fit less reliable Small sample size Nonlinear data Data spread over small range