LINE AND SLOPE Introduction Some examples of surfaces

LINE AND SLOPE

Introduction • Some examples of surfaces that slope are mountain, wheelchair ramp, and house roofs • Lengths of a line segment are always positive (+) 19 cm Line Segment

Slope • The slope of a line measures how steep it is • In this graph, you can see that line 2 is steeper than line 1 • If the line falls from left to right, they have negative slopes (as shown in the example) • If the line rises from left to right, it has a positive slope

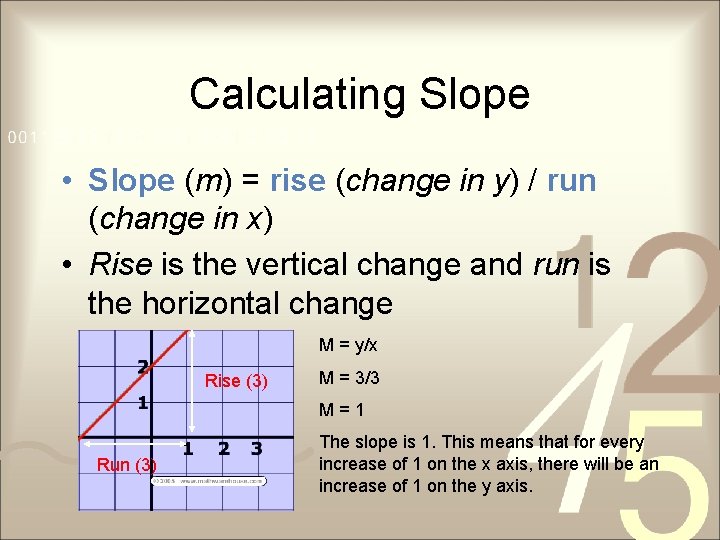
Calculating Slope • Slope (m) = rise (change in y) / run (change in x) • Rise is the vertical change and run is the horizontal change M = y/x Rise (3) M = 3/3 M=1 Run (3) The slope is 1. This means that for every increase of 1 on the x axis, there will be an increase of 1 on the y axis.

Calculating Slope • Another formula to calculate slope is m = Dy / Dx • Dy means (y 2 – y 1) • Dx means (x 2 – x 1) • Lines with positive slopes have positive numerical slopes • Lines with negative slopes have negative numerical slopes

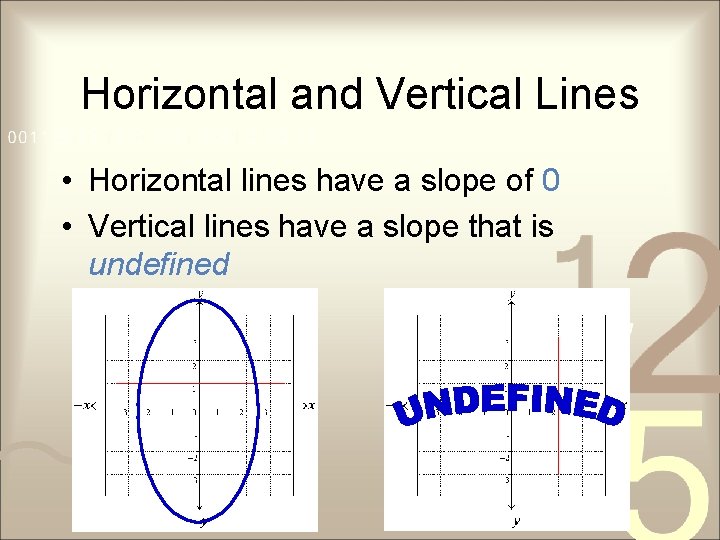
Horizontal and Vertical Lines • Horizontal lines have a slope of 0 • Vertical lines have a slope that is undefined

Point-Slope and Standard Form • There are 2 ways to find the equation of a line • One is the standard form, which is ‘Ax + By + C=0 • A, B, and C can equal any real number. X is the x-intercept and Y is the y-intercept. • The other form is ‘y-y 1 = m(x-x 1)’ • Plug in the coordinates of the first point for x 1 and y 1

X- and Y- Intercepts • Y-intercept is the point where the line crosses the y-axis • X-intercept is the point where the line crosses the x-axis

Slope and Y-Intercept Form • A third way to find the equation of a line is slope and y-intercept form • The equation is ‘Y= mx + b’

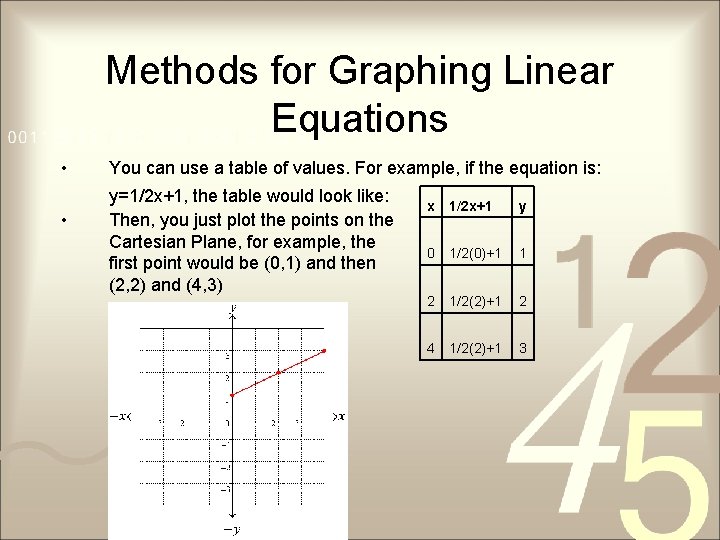
Methods for Graphing Linear Equations • • You can use a table of values. For example, if the equation is: y=1/2 x+1, the table would look like: Then, you just plot the points on the Cartesian Plane, for example, the first point would be (0, 1) and then (2, 2) and (4, 3) x 1/2 x+1 y 0 1/2(0)+1 1 2 1/2(2)+1 2 4 1/2(2)+1 3

Parallel and Perpendicular Lines • If 2 lines are parallel, they will have the same slope (m 1 = m 2) • All vertical lines are parallel • If 2 lines are parallel, their slopes multiplied by each other will equal -1 (this is called a negative reciprocal)

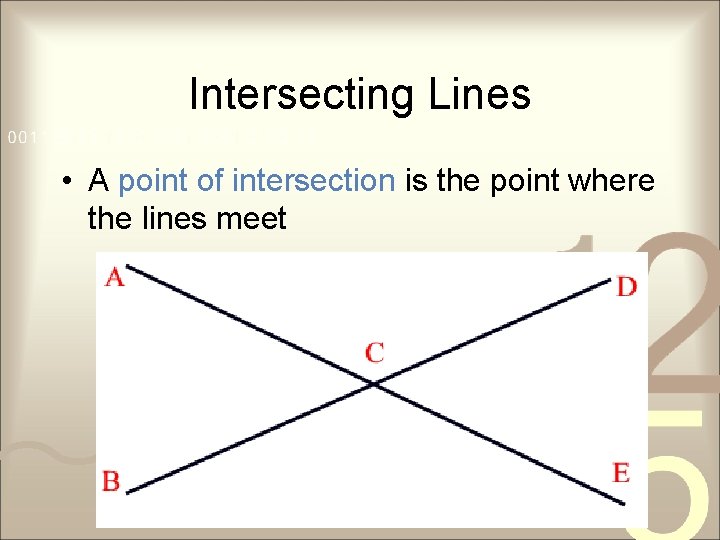
Intersecting Lines • A point of intersection is the point where the lines meet