Line and Curve Drawing Algorithms Line Drawing m1

Line and Curve Drawing Algorithms

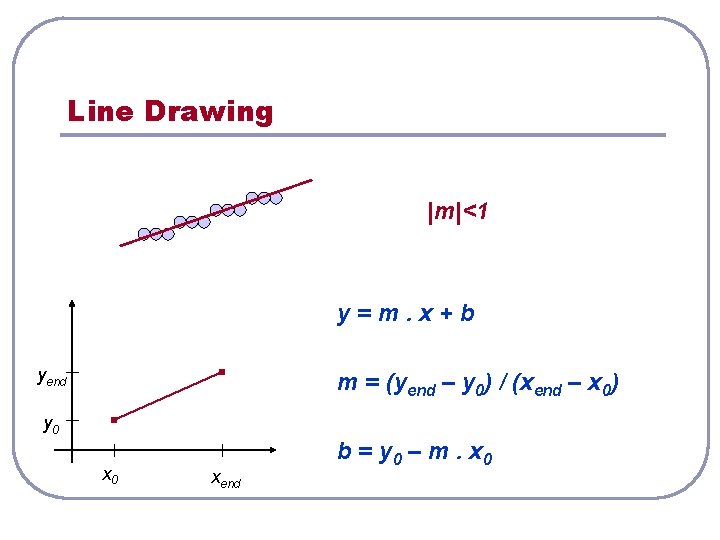
Line Drawing |m|<1 y=m. x+b yend m = (yend – y 0) / (xend – x 0) y 0 xend b = y 0 – m. x 0

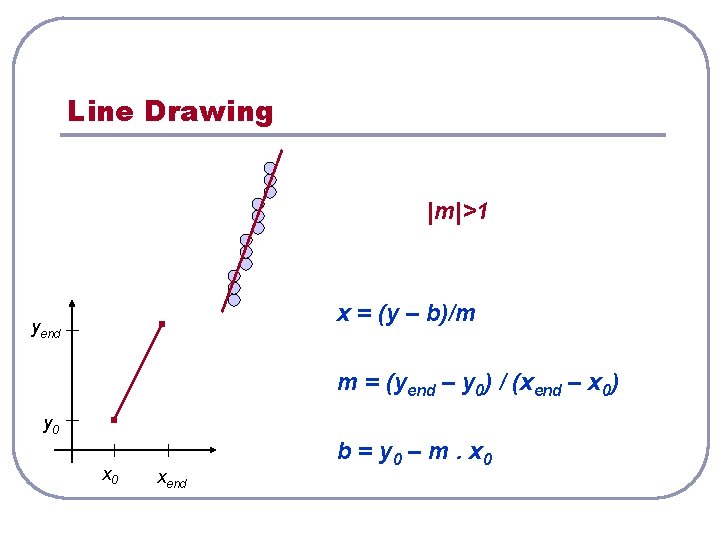
Line Drawing |m|>1 x = (y – b)/m yend m = (yend – y 0) / (xend – x 0) y 0 xend b = y 0 – m. x 0

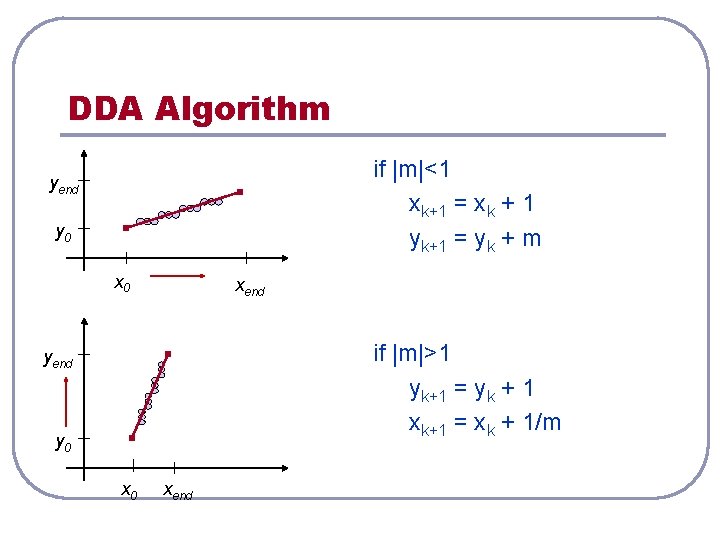
DDA Algorithm if |m|<1 xk+1 = xk + 1 yk+1 = yk + m yend y 0 xend if |m|>1 yk+1 = yk + 1 xk+1 = xk + 1/m yend y 0 xend

DDA Algorithm #include <stdlib. h> #include <math. h> inline int round (const float a) { return int (a + 0. 5); } void line. DDA (int x 0, int y 0, int x. End, int y. End) { int dx = x. End - x 0, dy = y. End - y 0, steps, k; float x. Increment, y. Increment, x = x 0, y = y 0; if (fabs (dx) > fabs (dy)) steps = fabs (dx); /* |m|<1 */ else steps = fabs (dy); /* |m|>=1 */ x. Increment = float (dx) / float (steps); y. Increment = float (dy) / float (steps); set. Pixel (round (x), round (y)); for (k = 0; k < steps; k++) { x += x. Increment; y += y. Increment; set. Pixel (round (x), round (y)); } }

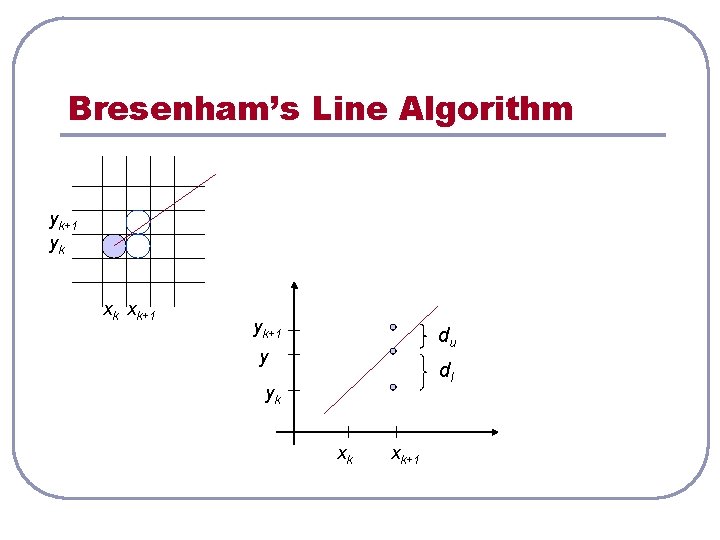
Bresenham’s Line Algorithm yk+1 yk xk xk+1 yk+1 du y dl yk xk xk+1

Bresenham’s Line Algorithm #include <stdlib. h> #include <math. h> /* Bresenham line-drawing procedure for |m|<1. 0 */ else { x = x 0; y = y 0; } set. Pixel (x, y); void line. Bres (int x 0, int y 0, int x. End, int y. End) { int dx = fabs(x. End - x 0), dy = fabs(y. End - y 0); int p = 2 * dy - dx; int two. Dy = 2 * dy, two. Dy. Minus. Dx = 2 * (dy - dx); int x, y; /* Determine which endpoint to use as start position. */ if (x 0 > x. End) { x = x. End; y = y. End; x. End = x 0; } while (x < x. End) { x++; if (p < 0) p += two. Dy; else { y++; p += two. Dy. Minus. Dx; } set. Pixel (x, y); } }

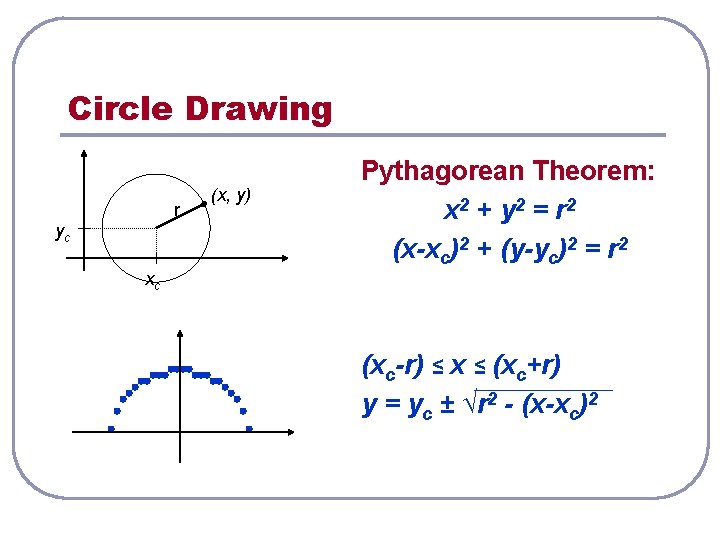
Circle Drawing r yc (x, y) Pythagorean Theorem: x 2 + y 2 = r 2 (x-xc)2 + (y-yc)2 = r 2 xc (xc-r) ≤ x ≤ (xc+r) y = yc ± √r 2 - (x-xc)2

Circle Drawing change x change y

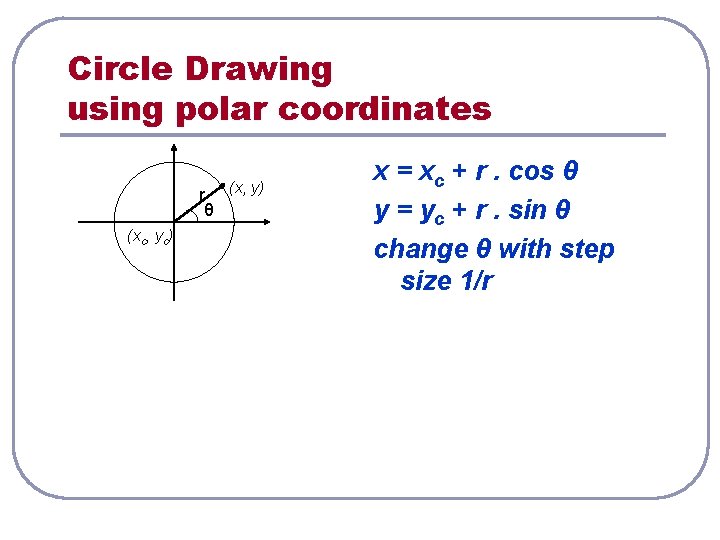
Circle Drawing using polar coordinates r (x, y) θ (xc, yc) x = xc + r. cos θ y = yc + r. sin θ change θ with step size 1/r

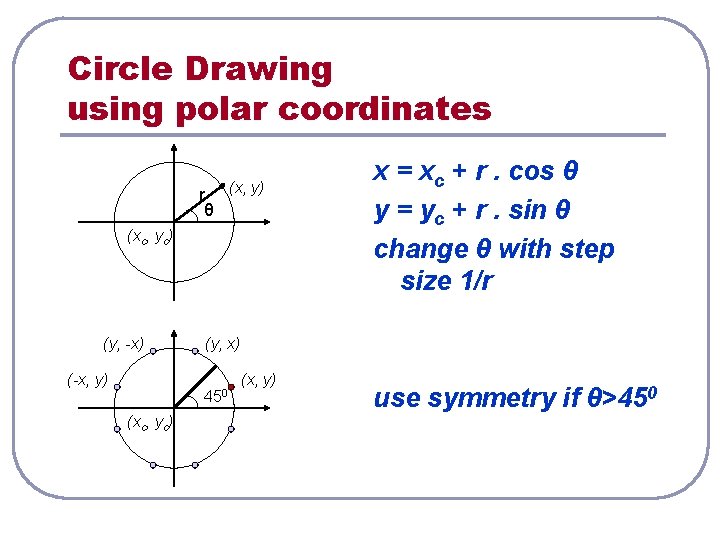
Circle Drawing using polar coordinates r (x, y) θ (xc, yc) (y, -x) (-x, y) (y, x) 450 (xc, yc) x = xc + r. cos θ y = yc + r. sin θ change θ with step size 1/r (x, y) use symmetry if θ>450

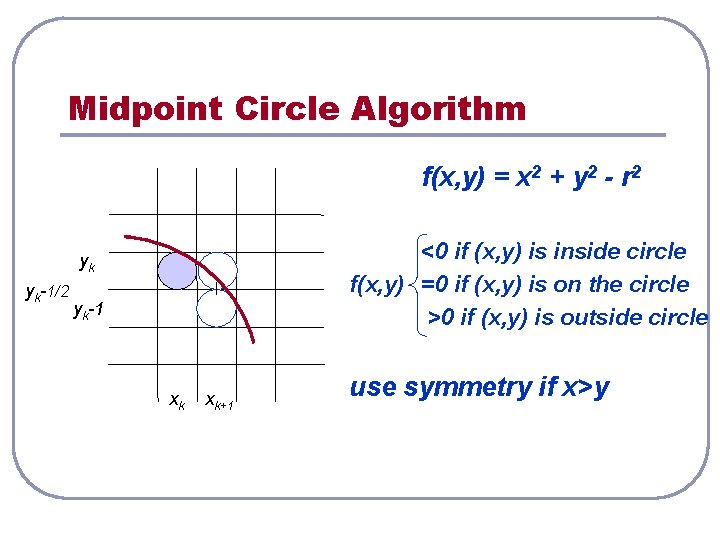
Midpoint Circle Algorithm f(x, y) = x 2 + y 2 - r 2 <0 if (x, y) is inside circle f(x, y) =0 if (x, y) is on the circle >0 if (x, y) is outside circle yk yk-1/2 yk-1 xk xk+1 use symmetry if x>y

Midpoint Circle Algorithm #include <GL/glut. h> class scr. Pt { public: GLint x, y; }; void set. Pixel (GLint x, GLint y) { gl. Begin (GL_POINTS); gl. Vertex 2 i (x, y); gl. End ( ); } void circle. Midpoint (scr. Pt circ. Ctr, GLint radius) { scr. Pt circ. Pt; GLint p = 1 - radius; circ. Pt. x = 0; circ. Pt. y = radius; void circle. Plot. Points (scr. Pt, scr. Pt); /* Plot the initial point in each circle quadrant. */ circle. Plot. Points (circ. Ctr, circ. Pt); /* Calculate next points and plot in each octant. */ while (circ. Pt. x < circ. Pt. y) { circ. Pt. x++; if (p < 0) p += 2 * circ. Pt. x + 1; else { circ. Pt. y--; p += 2 * (circ. Pt. x - circ. Pt. y) + 1; } circle. Plot. Points (circ. Ctr, circ. Pt); } } void circle. Plot. Points (scr. Pt circ. Ctr, scr. Pt circ. Pt); { set. Pixel (circ. Ctr. x + circ. Pt. x, circ. Ctr. y + circ. Pt. y); set. Pixel (circ. Ctr. x - circ. Pt. x, circ. Ctr. y + circ. Pt. y); set. Pixel (circ. Ctr. x + circ. Pt. x, circ. Ctr. y - circ. Pt. y); set. Pixel (circ. Ctr. x - circ. Pt. x, circ. Ctr. y - circ. Pt. y); set. Pixel (circ. Ctr. x + circ. Pt. y, circ. Ctr. y + circ. Pt. x); set. Pixel (circ. Ctr. x - circ. Pt. y, circ. Ctr. y + circ. Pt. x); set. Pixel (circ. Ctr. x + circ. Pt. y, circ. Ctr. y - circ. Pt. x); set. Pixel (circ. Ctr. x - circ. Pt. y, circ. Ctr. y - circ. Pt. x); }

Open. GL #include <GL/glut. h> // (or others, depending on the system in use) void init (void) { gl. Clear. Color (1. 0, 0. 0); // Set display-window color to white. gl. Matrix. Mode (GL_PROJECTION); // Set projection parameters. glu. Ortho 2 D (0. 0, 200. 0, 150. 0); } void line. Segment (void) { gl. Clear (GL_COLOR_BUFFER_BIT); gl. Color 3 f (0. 0, 1. 0); gl. Begin (GL_LINES); gl. Vertex 2 i (180, 15); gl. Vertex 2 i (10, 145); gl. End ( ); gl. Flush ( ); // Clear display window. // Set line segment color to blue. // Specify line-segment geometry. // Process all Open. GL routines as quickly as possible. } void main (int argc, char** argv) { glut. Init (&argc, argv); // Initialize GLUT. glut. Init. Display. Mode (GLUT_SINGLE | GLUT_RGB); // Set display mode. glut. Init. Window. Position (50, 100); // Set top-left display-window position. glut. Init. Window. Size (400, 300); // Set display-window width and height. glut. Create. Window ("An Example Open. GL Program"); // Create display window. init ( ); glut. Display. Func (line. Segment); glut. Main. Loop ( ); } // Execute initialization procedure. // Send graphics to display window. // Display everything and wait.

Open. GL Point Functions • gl. Vertex*( ); * : 2, 3, 4 i (integer) s (short) f (float) d (double) Ex: gl. Begin(GL_POINTS); gl. Vertex 2 i(50, 100); gl. End(); int p 1[ ]={50, 100}; gl. Begin(GL_POINTS); gl. Vertex 2 iv(p 1); gl. End();

Open. GL Line Functions • • • GL_LINES GL_LINE_STRIP GL_LINE_LOOP Ex: gl. Begin(GL_LINES); gl. Vertex 2 iv(p 1); gl. Vertex 2 iv(p 2); gl. End();

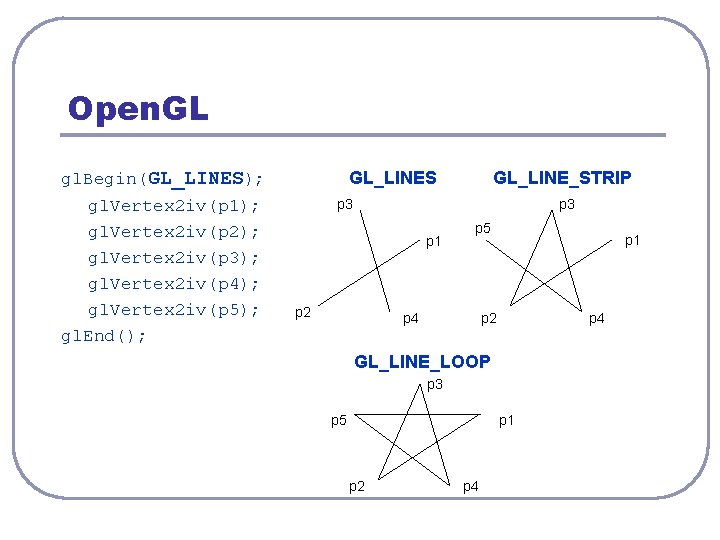
Open. GL gl. Begin(GL_LINES); gl. Vertex 2 iv(p 1); gl. Vertex 2 iv(p 2); gl. Vertex 2 iv(p 3); gl. Vertex 2 iv(p 4); gl. Vertex 2 iv(p 5); gl. End(); GL_LINES GL_LINE_STRIP p 3 p 1 p 2 p 5 p 4 p 1 p 2 p 4 GL_LINE_LOOP p 3 p 5 p 1 p 2 p 4

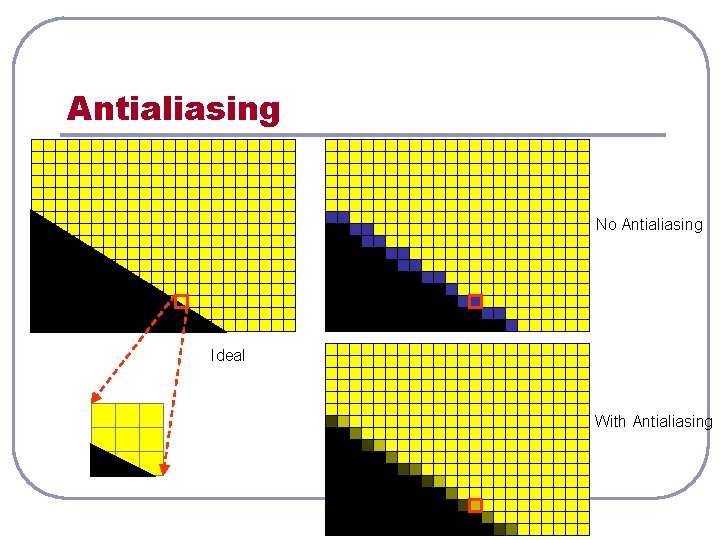
Antialiasing No Antialiasing Ideal With Antialiasing

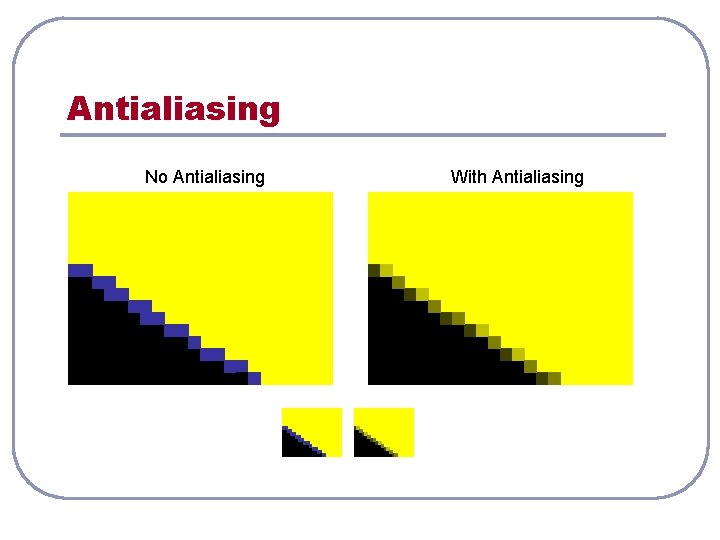
Antialiasing No Antialiasing With Antialiasing

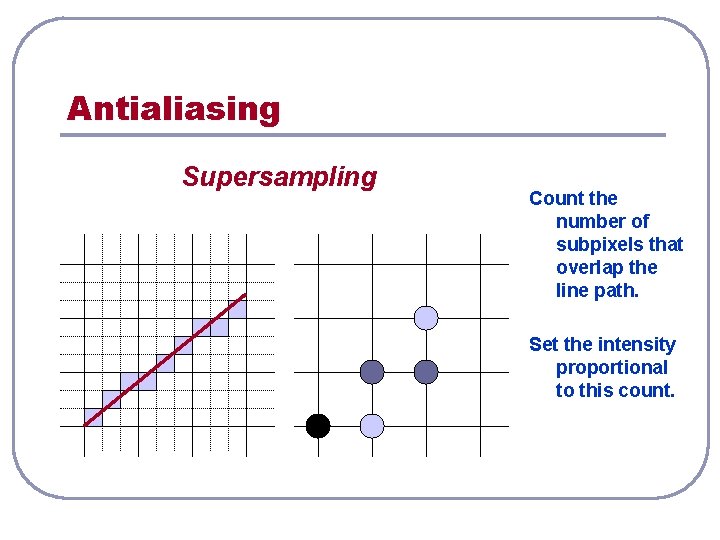
Antialiasing Supersampling Count the number of subpixels that overlap the line path. Set the intensity proportional to this count.

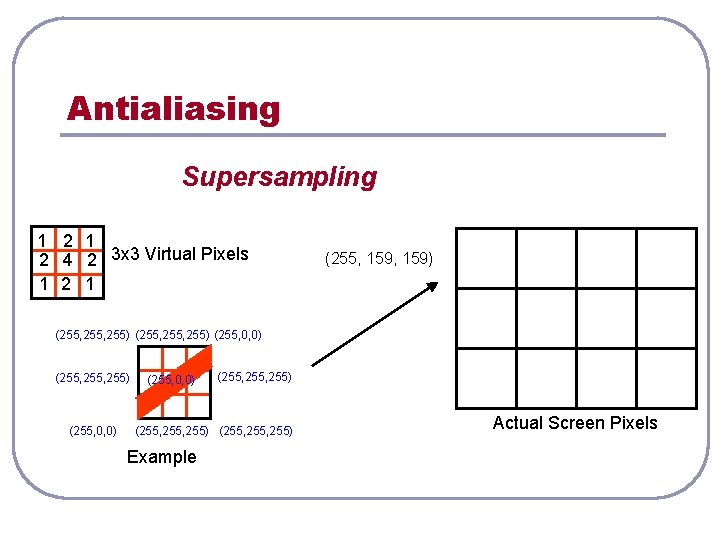
Antialiasing Supersampling 1 2 4 2 3 x 3 Virtual Pixels 1 2 1 (255, 159) (255, 255) (255, 0, 0) (255, 255, 255) (255, 255) Example Actual Screen Pixels

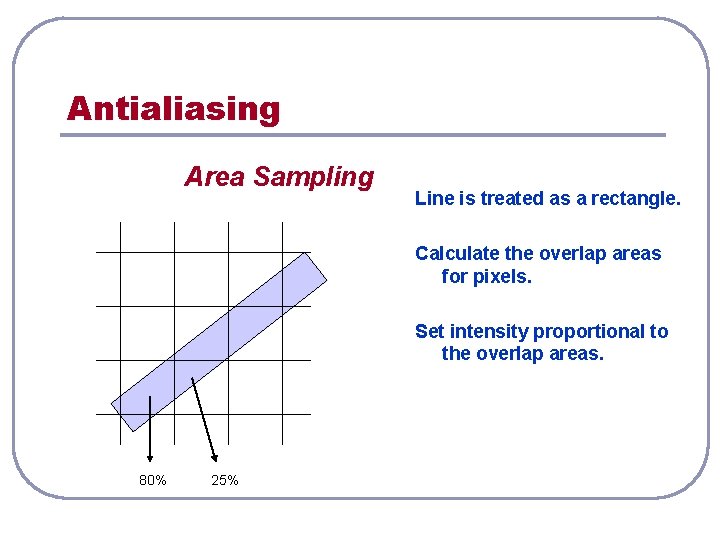
Antialiasing Area Sampling Line is treated as a rectangle. Calculate the overlap areas for pixels. Set intensity proportional to the overlap areas. 80% 25%

Antialiasing Pixel Sampling Micropositioning Electron beam is shifted 1/2, 1/4, 3/4 of a pixel diameter.

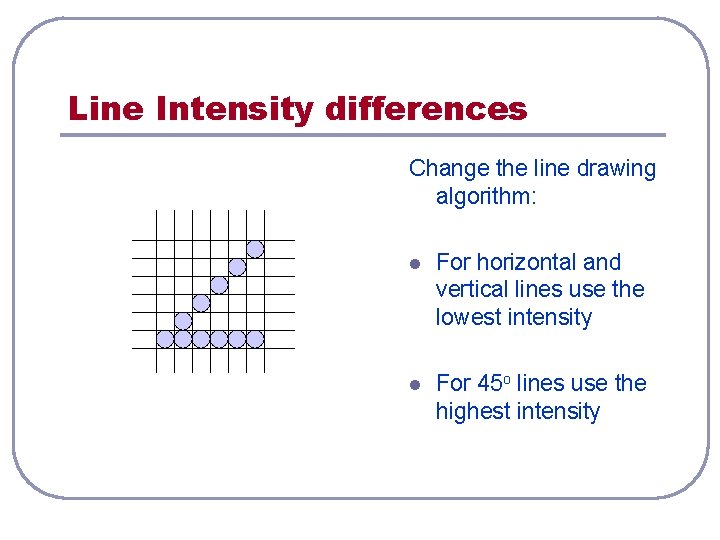
Line Intensity differences Change the line drawing algorithm: l For horizontal and vertical lines use the lowest intensity l For 45 o lines use the highest intensity