Line and Circle Drawing Algorithms 10102006 1 Learning

Line and Circle Drawing Algorithms 10/10/2006 1

Learning Objectives • • Coordinate reference frames Two-dimensional world reference Point functions Line drawing algorithms Curve functions Circle algorithms Other algorithms 10/10/2006 2

Learning Objectives • Understand Point and Line geometric primitives. • Understand line drawing algorithm. • Understand circle drawing algorithms. 10/10/2006 3

Graphics Output Primitives • Graphics output primitives – Functions used to describe the various picture components – Examples: car, house, flower, … • Geometric primitives – Functions used to describe points, lines, triangles, circles, … 10/10/2006 4

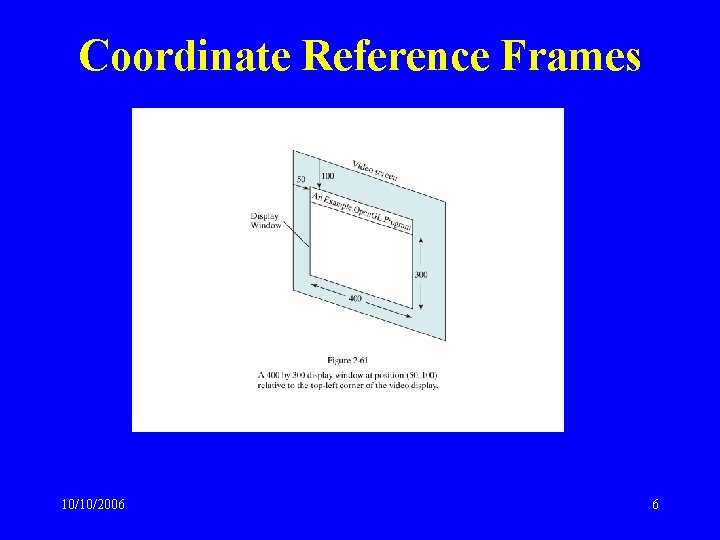
Coordinate Reference Frames • Cartesian coordinate system – Can be 2 D or 3 D – Objects are associated with a set of coordinates – World coordinates are associated with a scene • Object description – Coordinates of vertices – Color – Coordinate extents (min and max for each (x, y, z) in object – also called the bounding box • In 2 D – bounding rectangle 10/10/2006 5

Coordinate Reference Frames 10/10/2006 6

Coordinate Reference Frames • Screen coordinates – Location of object on a monitor – Start from upper left corner (origin (0, 0)) – Pixel coordinates • Scan line number (y) • Column number (x) – Other origin lower left corner (0, 0) – Pixel coordinate references the center of the pixel • set. Pixel (x, y) • get. Pixel (x, y, color) • Depth value is 0 in 2 D 10/10/2006 7

Coordinate Reference Frames • Relative coordinates – Current position – Offset from the current position – Example • Current position (2, 3) • Relative coordinates (4, -1) • Absolute coordinates (6, 2) 10/10/2006 8

2 D World Reference 10/10/2006 9

2 D World Reference • glu. Ortho 2 D (x. Min, x. Max, y. Min, y. Max) – References display window as a rectangle with the minimum and maximum values listed – Absolute coordinates within these ranges will be displayed gl. Matrix. Mode(GL. GL_PROJECTION); // set current matrix to projection matrix gl. Load. Identity(); // sets projection matrix to identity glu. Ortho 2 D(0. 0, 200. 0, 150. 0); // set coordinate values // with vertices (0, 0) for lower left corner // and (200, 150) for upper right corner 10/10/2006 10

2 D World Reference • Open. GL matrices – Control how images are rendered – Three matrices 4 x 4 – Stored differently than in maths – lines and columns are inversed (transposed matrices) – Projection matrix describes how the vertex coordinates are displayed on the screen, based on field of view and near and far planes – Modelview matrix is applied to each vertex coordinate and modifies their locations – Texture matrix is used to manipulate how textures are drawn on objects – default set to identity 10/10/2006 11

2 D World Reference • Orthographic projection is standard in the projection matrix – gl. Matrix. Mode(GL. GL_PROJECTION) select the projection matrix – gl. Load. Identity() set this matrix to the identity matrix – gl. Ortho 2 D(0, 200, 0, 150) sets the coordinate values on display between (0, 0) and (200, 150) 10/10/2006 12

Point Functions • Point – Coordinates – Color - gl. Color 3 f(1. 0 f, 0. 0 f ); RGB – Size – one screen pixel by default (gl. Point. Size) – gl. Begin (GL. GL_POINTS) gl. Vertex 2 i (50, 100); gl. Vertex 2 i (75, 150); gl. End(); – Coordinates can also be set in an int []: int point 1 [] = {50, 100}; … gl. Vertex 2 iv (point 1); – Point class can also be used (Point(x, y), get. X(), get. Y(), set. Location(50, 100), …). 10/10/2006 13

Line Functions • Line – Defined by two endpoint coordinates (one line segment) gl. Begin( GL. GL_LINES ); gl. Vertex 2 i( 180, 15 ); gl. Vertex 2 i( 10, 145 ); gl. End(); – If several vertices, a line is drawn between the first and second, then a separate one between the third and the fourth, etc. (isolated vertices are not drawn). 10/10/2006 14

Line Functions • Polyline – Defined by line connecting all the points gl. Begin( GL. GL_LINE_STRIP gl. Vertex 2 i( 180, 15 gl. Vertex 2 i( 10, 145 gl. Vertex 2 i( 100, 20 gl. Vertex 2 i( 30, 150 gl. End(); ); ); ); – Draws a line between vertex 1 and vertex 2 then between vertex 2 and vertex 3 then between vertex 3 and vertex 4. 10/10/2006 15

Line Functions • Polyline – Adds a line between the last vertex and the first one gl. Begin( GL. GL_LINE_LOOP ); gl. Vertex 2 i( 180, 15 ); gl. Vertex 2 i( 10, 145 ); gl. Vertex 2 i( 100, 20 ); gl. Vertex 2 i( 30, 150 ); gl. End(); – Draws a line between vertex 1 and vertex 2 then between vertex 2 and vertex 3 then between vertex 3 and vertex 4 then between vertex 4 and vertex 1. 10/10/2006 16

Line Drawing Algorithms • Line drawn as pixels • Graphics system – Projects the endpoints to their pixel locations in the frame buffer (screen coordinates as integers) – Finds a path of pixels between the two – Loads the color – Plots the line on the monitor from frame buffer (video controller) – Rounding causes all lines except horizontal or vertical to be displayed as jigsaw appearance (low resolution) – Improvement: high resolution, or adjust pixel intensities on the line path. 10/10/2006 17

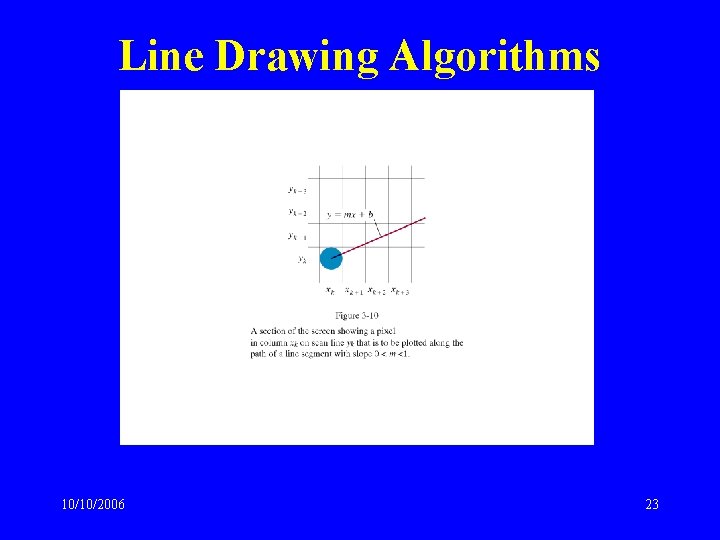
Line Drawing Algorithms • Line equation – Slope-intercept form y=m. x+b slope m Y-intercept b – Slope – Y-intercept 10/10/2006 18

Line Drawing Algorithms • DDA (Digital Differential Analyzer) – Scan conversion line algorithm – Line sampled at regular intervals of x, then corresponding y is calculated – From left to right 10/10/2006 19

Line Drawing Algorithms void line. DDA (int x 0, int y 0, int x. End, int y. End) { int dx = x. End - x 0, dy = y. End - y 0, steps, k; float x. Increment, y. Increment, x = x 0, y = y 0; if (fabs (dx) > fabs (dy)) steps = fabs (dx); else steps = fabs (dy); x. Increment = float (dx) / float (steps); y. Increment = float (dy) / float (steps); set. Pixel (round (x), round (y)); for (k = 0; k < steps; k++) { x += x. Increment; y += y. Increment; set. Pixel (round (x), round (y)); } } 10/10/2006 20

Line Drawing Algorithms • Advantage – Does not calculate coordinates based on the complete equation (uses offset method) • Disadvantage – Round-off errors are accumulated, thus line diverges more and more from straight line – Round-off operations take time • Perform integer arithmetic by storing float as integers in numerator and denominator and performing integer artithmetic. 10/10/2006 21

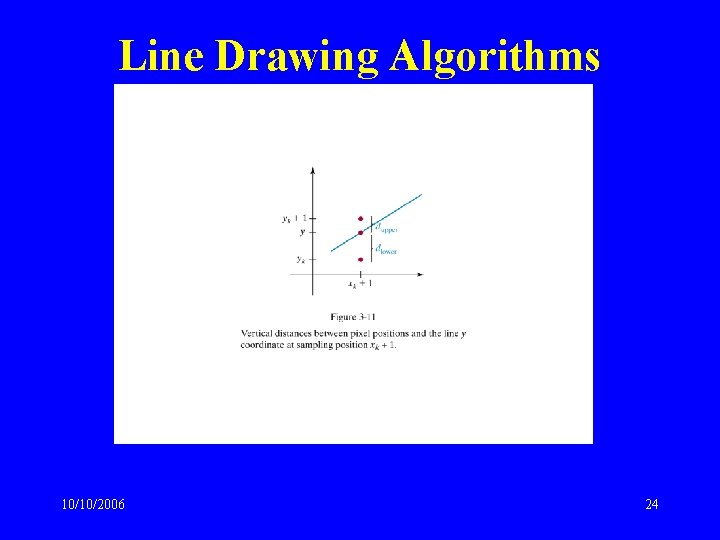
Line Drawing Algorithms • Bresenham’s line drawing – Efficient line drawing algorithm using only incremental integer calculations – Can be adapted to draw circles and other curves • Principle – Vertical axes show scan line positions – Horizontal axes show pixel columns – At each step, determine the best next pixel based on the sign of an integer parameter whose value is proportional to the difference between the vertical separations of the two pixel positions from the actual line. 10/10/2006 22

Line Drawing Algorithms 10/10/2006 23

Line Drawing Algorithms 10/10/2006 24

Line Drawing Algorithms • Bresenham’s line drawing algorithm (positive slope less than 1) dlower = y – yk dupper = (yk + 1) – y dlower – dupper = 2 m(xk+1) – 2 yk + 2 b – 1 decision parameter: pk= Δx (dlower – dupper ) pk = 2Δy xk- 2Δx yk + c sign of pk is the same as sign of dlower – dupper 10/10/2006 25

Line Drawing Algorithms • Bresenham’s line drawing algorithm (positive slope less than 1 1. 2. 3. 4. 5. 10/10/2006 Input the two line endpoints and store the left endpoint in (x 0, y 0). Set the color for the frame-buffer position (x 0, y 0) – i. e. plot the first point. Calculate the constant 2Δy –Δx, and set the starting value for the decision parameter as p 0 = 2Δy –Δx. At each xk along the line, from k=0, perform the following test: if pk<0, next point to plot is (xk + 1, yk) and pk+1 = pk + 2Δy otherwise, next point to plot is (xk + 1, yk + 1 ) and pk+1 = pk + 2Δy- 2Δx Repeat step 4 Δx - 1 times. 26

Curve Functions • Such primitive functions as to display circles and ellipses are not provided in Open. GL core library. • GLU has primitives to display spheres, cylinders, rational B-splines, including simple Bezier curves. • GLUT has some of these primitives too. • Circles and ellipses can also be generated by approximating them using a polyline. • Can also be generated by writing own circle or ellipsis display algorithm. 10/10/2006 27

Curve Functions 10/10/2006 28

Circle Algorithms • Properties of circles: 10/10/2006 29

Circle Algorithms • Polar coordinates • Symmetry of circles • All these methods have long execution time 10/10/2006 30

Curve Functions 10/10/2006 31

Curve Functions 10/10/2006 32

Circle Algorithms • Principle of the midpoint algorithm – Reason from octants of a circle centered in (0, 0), then find the remaining octants by symmetry, then translate to (xc, yc). – The circle function is the decision parameter. – Calculate the circle function for the midpoint between two pixels. 10/10/2006 33

Circle Algorithms • Midpoint circle drawing algorithm 1. Input radius r and circle center (xc, yc), then set the coordinates for the first point on the circumference of a circle centered on the origin as (xo, y 0) = (0, r). 2. Calculate the initial value of the decision parameter as p 0 = 5/4 – r (1 – r if an integer) 3. At each xk, from k=0, perform the following test: if pk<0, next point to plot along the circle centered on (0, 0) is (xk + 1, yk) and pk+1 = pk + 2 xk+1 + 1 otherwise, next point to plot is (xk+ 1, yk - 1) and pk+1 = pk + 2 xk+1 + 1 - 2 yk+1 where 2 xk+1 = 2 xk + 2, and 2 yk+1 = 2 yk - 2 10/10/2006 34

Circle Algorithms • Midpoint circle drawing algorithm 4. Determine symmetry points in the other seven octants. 5. Move each calculated pixel position (x, y) onto the circular path centered at (xc, yc) and plot the coordinate values: x = x + x c, y = y + y c 6. Repeat steps 3 through 5 until x >= y. 10/10/2006 35

Curve Functions • • Ellipsis can be drawn similarly using a modified midpoint algorithm. Similar algorithms can be used to display polynomials, exponential functions, trigonometric functions, conics, probability distributions, etc. 10/10/2006 36

Curve Functions 10/10/2006 37

Curve Functions 10/10/2006 38

Curve Functions 10/10/2006 39