Linda A Dataspace Approach to Parallel Programming CSE

Linda: A Data-space Approach to Parallel Programming CSE 60771 – Distributed Systems David Moore

Problem: How to Implement Parallel Algorithms Naturally � Classic approaches to parallel programming are clunky and difficult to use for many tasks � Logically concurrent algorithms benefit immensely from simultaneous threads of computation � Distributed systems seek the utility of interconnected, yet independent subsystems � Linda simplifies the task of writing parallel programs

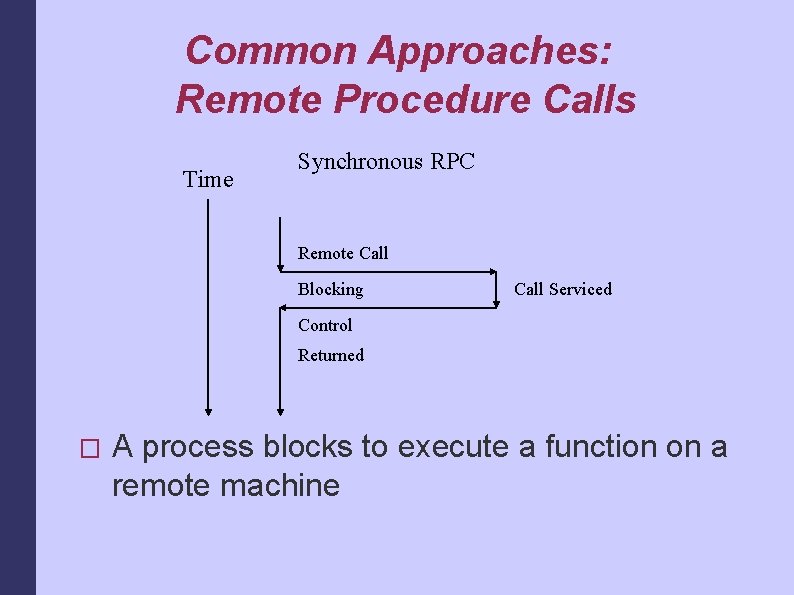
Common Approaches: Remote Procedure Calls Time Synchronous RPC Remote Call Blocking Call Serviced Control Returned � A process blocks to execute a function on a remote machine

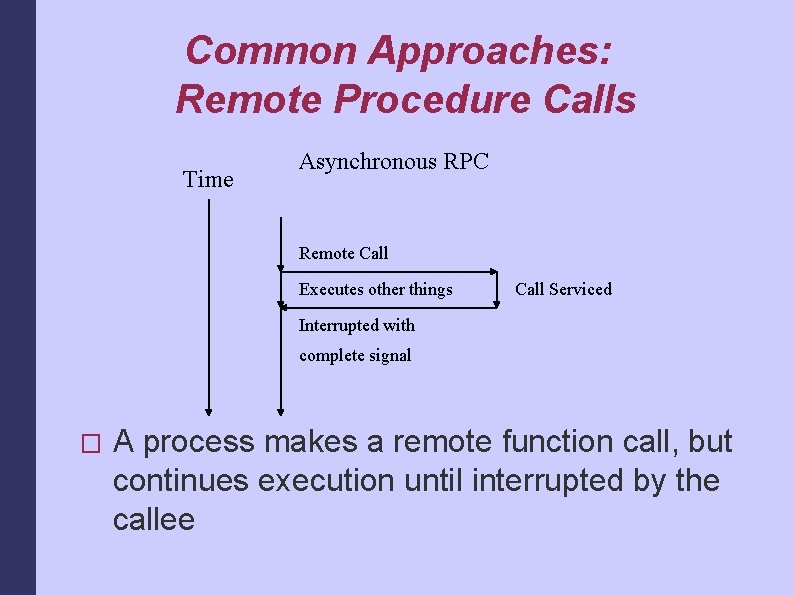
Common Approaches: Remote Procedure Calls Time Asynchronous RPC Remote Call Executes other things Call Serviced Interrupted with complete signal � A process makes a remote function call, but continues execution until interrupted by the callee

Common Approaches: Message Passing Time Information Passed � Systems may send, check, and wait for messages from specified peers

A New Approach � RPC and Message-passing are limited: � � � One to one communication RPC – control transfers Message-passing – data is transient Linda provides a metaphor that is parallel in nature, multi-node in scope, does not relinquish the processor, and preserves data. � Its spirit is a shared data-space �

Overview of Linda Provides shared-memory style interface � Extends existing programming languages � Adds 3 commands: in, out, and read � Alters syntax slightly, hence requiring language changes, not just a library addition � Implemented extensions include C and Fortran �

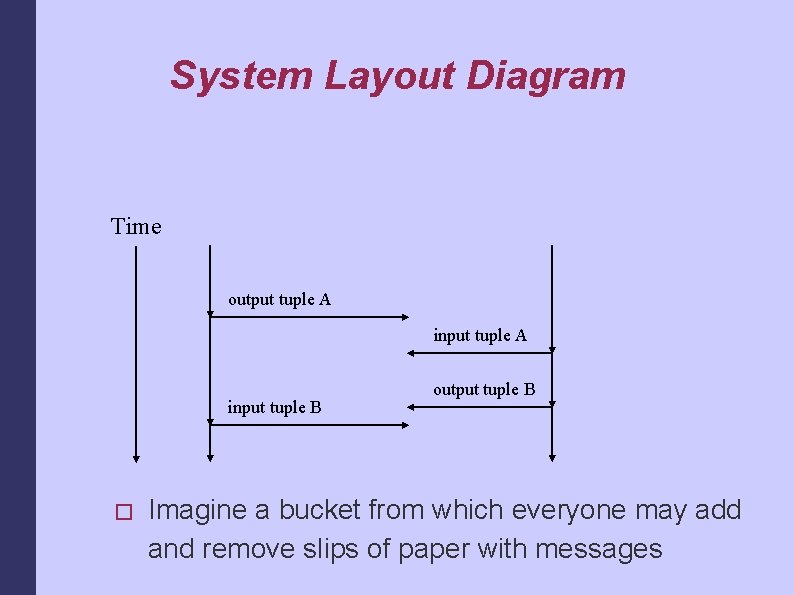
System Layout � Linda provides a network accessible “Tuple Space”. � Any node in the network may add, read, and remove information to and from the shared space in the form of tuples. � Done via output, input, and read commands. � A tuple contains a key, and one or more fields of data. � This is an example of a data-space architecture.

System Layout Diagram Time output tuple A input tuple B � output tuple B Imagine a bucket from which everyone may add and remove slips of paper with messages

Out() Command: Writing a Tuple to the TS � out(logical name, data 1 [, data 2, . . . ]); � � // If int a, char b, and long c are defined out(a, b, c); //Add a tuple to the TS named to a's value, containing the information in b and c out('A', b, 7); //Add a tuple to the TS with 'A' as its name, containing b's value and the value 7 No restriction on multiple tuples with the same name or data � All arguments must be of unambiguous type � For every tuple field, both value and type are stored � If both int b and char b existed, we must make a distinction

In() Command: Retrieving a Tuple from the TS � in(logical name, <argument list>); Valid arguments: � type and target variable – if a tuple matching the logical name and with a field in this position with this type exists, that field's value is put in the target variable � matching variable or constant– restricts the set of tuples considered to be read to those whose value in this field matches the value provided � If there is more than one match, selection is arbitrary � This command removes from the TS any tuple it returns. � This command suspends until a matching tuple if found � A type and variable name as an argument violate standard C structure. The is the reason it cannot be library-implemented. �

In() Command: Examples If these tuples are in the TS � 'P', 5, 8 � 'P', 4, 7 � 'P', 'S' � Valid commands and results � in('P', int a, int b); //either a=5, b=8, or (arbitrarily) a=4, b=7 � in('P', int a, 8); //a=5 � in('P', char c); //c = 'S' � in('P', char c, int a); //block until a (char, int) tuple is added to the TS �

Read() Command: Examining a Tuple in the TS � in(logical name, <argument list>); � � Same arguments as in(); Same results, except the tuple is not removed from the Tuple Space.

Implementation � Each node in the network maintains a copy of the TS. � out() and read(): the simple cases out() � Transmit to all nodes the tuple to be added � Each node adds it to their local TS cache � Constant time operation assuming a multi-cast command � read() � Examine the local TS cache � Find any tuple that matches the specified types, and possibly specified values if given. � Return its data. � Order O(tuple_count) operation � Searches and tuples are complex, hence keying, hashing, and sorting cannot improve search time �

Implementation � in(), while similar to read(), requires a node-wide deletion � First search the local TS cache for a matching tuple � If not found, block until one is added � If found, contact the tuple's originator � Obtain permission from that node to delete � This prevents two nodes from performing simultaneous in()'s on the same tuple � Inform all nodes of the deletion � Return the data � Order O(tuple_count) operation �

Example #1: A Matrix Multiplier � Three Component Processes Initialization Process – Loads all input data into tuples by row or column in the TS. Spawns multiple workers and a cleanup process. � Worker Process � in()'s a “position tuple” indicating the next un-calculated cell in the solution matrix. � Stores its value, increments it, and replaces it into the TS. � Calculates the data for that cell, outputting the results to the TS. � Cleanup Process – Attempts to read in all the cells in the solution matrix, repeatedly blocking until all cells are obtained. �

Example #2: A Web Server � Initializer Process: Contacted by clients requesting files. Creates tuples containing the client's information and requested files. � Worker Process: Examines the TS for requests for files it is responsible for. Removes tuples fulfilling this requirement, and services the client requesting those files. � This would allow the addition of new files seamlessly, as new workers to handle the new files could be added without other system modifications. � To achieve this without changing the initializer, a clean-up process that deleted requests for non-existent files would be needed, and modified when new files became valid requests.

Hard Cases � This was implemented on AT&T's S/Net bus network: it was extremely reliable and reportedly never lost any information. Today's networks make no such guarantee, yet Linda makes no allowance for lost information. � All nodes require communication preprocessors to avoid interruption of their execution when tuples enter and leave the TS. � Large applications will create enormous TS's, possibly overloading network traffic and exhausting local storage on some nodes. � The failure or shutdown of a node prevents any tuples it added from being removed.

Hard Cases: S/Net Specifics Node 1 2 3 Node 4 5 VAX Supercompute r � Collection of up to 64 disjoint inexpensive nodes � Connected by a fast, word-parallel broadcast bus � The addition of new nodes is simple � May have a super-computer node, but not required � “Perfect” reliability � If input buffer is full on a node and it is forced to dump a message, it turns on a bus-wide negative acknowledgment signal, all transmitting nodes should repeat their messages until the signal ceases

Results: Linda's Performance � Hard Numbers: Linda was capable of 720 in-out pairs executed per second. � Effective performance: As the number of workers approaches the number of job sections, the time to complete the total task approaches the time for one worker to complete one job section. � System overhead is generally minimal in comparison to job time

Linda's Performance and Granularity of Parallelism � If a job has 10 segments and 5 workers it takes as long with 9 workers. � If we subdivide the job further to avoid this problem, we incur additional overhead.

Overview � New approach to distributed computing � Shared data-space architecture � Assumes perfect reliability � Difficulty scaling to large data sets

Discussion What common tasks would be suited to this approach? � What are the effects and varieties of failure in the base Linda implementation? � How would Linda be implemented over the Internet? � What semantics of failure would this implementation present? �