LIMITS Chris Floyd Zach Hilley Aaron Hevenstone LIMITS

LIMITS Chris Floyd Zach Hilley Aaron Hevenstone

LIMITS A LIMIT IS THE VALUE A FUNCTION APPROACHES AT A CERTAIN POINT.

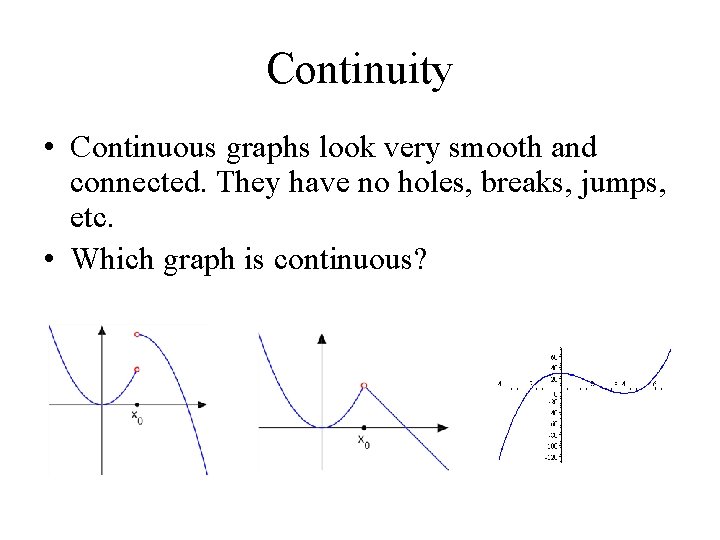
Is it continuous? Functions can have continuities, discontinuities, or even bothinuities. Testing for continuities within a function is similar to testing if a limit even exists! There are three different stipulations (big word!) that MUST be met in order for a function to be continuous.

Continuity • Continuous graphs look very smooth and connected. They have no holes, breaks, jumps, etc. • Which graph is continuous?

So… What does it really mean? • A function f(x) is continuous at x=c if THREE conditions are met: – Lim f(x) exists – f(c) is defined – Lim f(x)=f(c)

UH OH! It didn’t pass one of the three tests… • When a limit doesn’t meet one of the conditions, it has a discontinuity. • There are THREE main discontinuities: – Jump – usually a piecewise function whose pieces don’t meet up. – Point – When the function has a hole. (a “point” is missing!!!) – Infinite – When the function has neither a limit nor is defined at the given x-value. This is usually a vertical asymptote.

Removable vs. Nonremovable • A discontinuity can be labeled as removable when it is a “hole” in the function. In other words, it is when the limit is defined but the value f(c) is not. : ’( • A nonremovable continuity exists when the limit does not.

PRACTICE (CONTINUITY) Determine whether of not g(x) is continuous at x=1 3 x 2 -x-2 , x≠ 1 g(x)={ x-1 -2, x=1 Give all x-values for which the function is discontinuous, and classify each instance of discontinuity. g(x)=2 x 2+5 x-25 x 2 -25

Evaluating Limits The easiest way to evaluate a limit is simply to plug in the approached value to the function. lim x 2/(x+2)=? ? ? x -> 4 If you said 8/3 you are a winner! There a few situations where this method falls short. A limit may not exist, it may have an indeterminant form, or it may not be equal to the function.

HOW can a limit not equal the function!? ? Because a limit only means the value that a function approaches, the limit may be equal to a value different from that of the function, even if the function does not exist at that location.

One sided limits Limits can sometimes be taken from only one side of a point. If for example you are taking a limit from the right, you look at what the function approaches from the right side, sometimes limits from the right and left are different. In this case the limit does not exist.

When does a limit not exist? A limit does not exist if… The limit from the right does not equal the limit from the left. The limit approaches infinity. The function oscillates.

Approaching infinity If you are taking a limit of a function as it approaches infinity look at the degree of the numerator and denominator. If they are the same, then the limit is the ratio of the coefficients. If the degree of the numerator is greater, the function approaches infinity. If the degree of the denominator is greater, the function approaches 0.

Indeterminant forms If a limit approaches certain values that cannot be evaluated (but are NOT undefined!) like 0*infinity, 0/0, infinity/infinity, etc. then more work must be done to evaluate the limit. 1/0 IS NOT INDETERMINANT!

L’Hopital’s Rule (or Little Hospitals) L’Hopital’s Rule is a useful method for evaluating an indeterminant limit. To use Little Hospitals take the derivative of the numerator and the denominator separately (do not use division rule) and then evaluate the limit. This method will NOT work unless the limit is indeterminant.

Practice!

Intermediate Value Theorem • If a function f is continuous on a closed interval [a, b], and c is any number between f(a) and f(b) inclusive, then there is at least one number x in the closed interval such the f(x)=c.

Basically, if f(x) is continuous from on point, a, to another, b, then there is a point in between them, c.

Corollary • f(x) is continuous on [a, b] and if f(a) and f(b) are nonzero numbers and have opposite signs, f(x) has a zero in (a, b) • There’s a zero if it is continuous and goes from negative to positive.

Problems!

Asymptotes of Limits • The behavior of a function f(x) as either x or f(x) approaches positive or negative infinity. • There exists a vertical asymptote if the limit, as x approaches L from the right or left, of f(x) is positive or negative infinity. • There exists a horizontal asymptote if the limit, as x approaches positive or negative infinity, of f(x) equals L.

Fun Stuff • If the exponents of the variables in the numerator and the denominator are equal, then the limit approaches the coefficients of the variables. • If the exponent of the variable in the denominator is greater, then the limit approaches pos. or neg. infinity • If the exponent of the variable in the numerator is greater, then the limit approaches infinity.

More Problems!

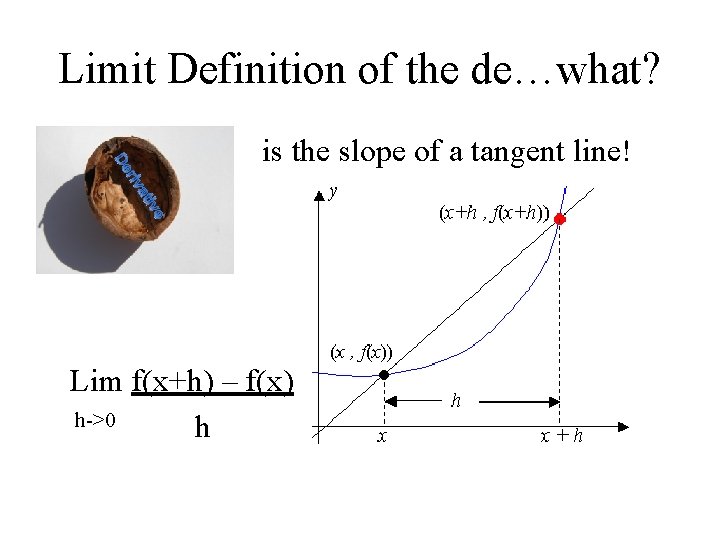
Limit Definition of the de…what? • is the slope of a tangent line! Lim f(x+h) – f(x) h->0 h

I’ve got problems… (Limit Definition) Find the derivative of f(x)=5 x 2+7 x -6 and use it to calculate f’(-1) Find the derivative of g(x)=x 2 -3 x +4 and then evaluate f’(2)