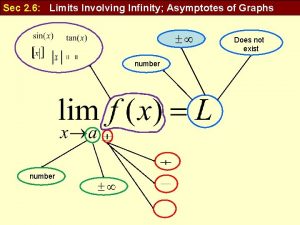
LIMITS AND DERIVATIVES 2 6 Limits at Infinity





























- Slides: 38

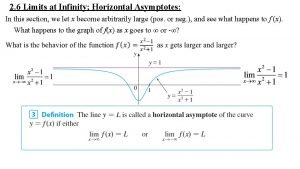
LIMITS AND DERIVATIVES. 2. 6 Limits at Infinity: Horizontal Asymptotes In this section, we: Let x become arbitrarily large (positive or negative) and see what happens to y.

HORIZONTAL ASYMPTOTES Let’s begin by investigating the behavior of the function f defined by as x becomes large.

HORIZONTAL ASYMPTOTES As x grows larger and larger, you can see that the values of f(x) get closer and closer to 1. § It seems that we can make the values of f(x) as close as we like to 1 by taking x sufficiently large.

HORIZONTAL ASYMPTOTES This situation is expressed symbolically by writing In general, we use the notation to indicate that the values of f(x) become closer and closer to L as x becomes larger and larger.

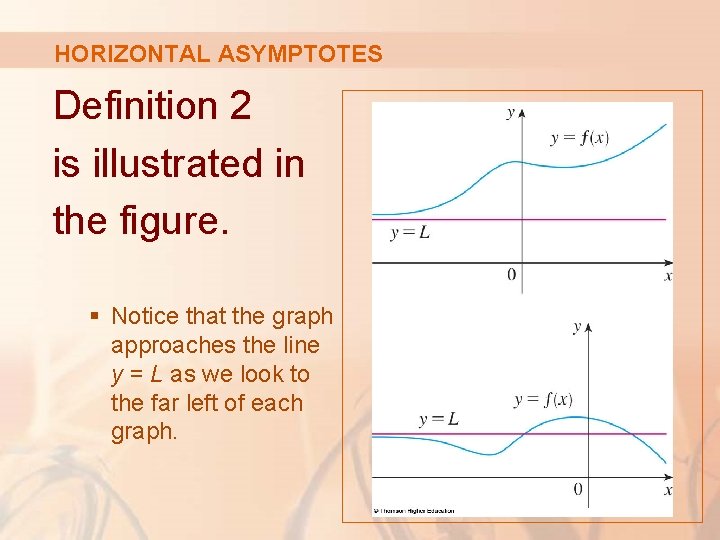
HORIZONTAL ASYMPTOTES 2. Definition Let f be a function defined on some interval. Then, means that the values of f(x) can be made arbitrarily close to L by taking x sufficiently large negative.

HORIZONTAL ASYMPTOTES Definition 2 is illustrated in the figure. § Notice that the graph approaches the line y = L as we look to the far left of each graph.

HORIZONTAL ASYMPTOTES 3. Definition The line y = L is called a horizontal asymptote of the curve y = f(x) if either

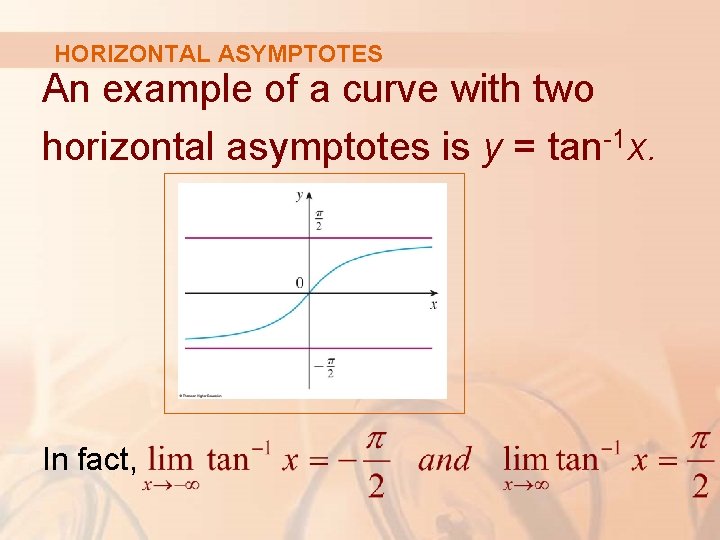
HORIZONTAL ASYMPTOTES An example of a curve with two horizontal asymptotes is y = tan-1 x. In fact,

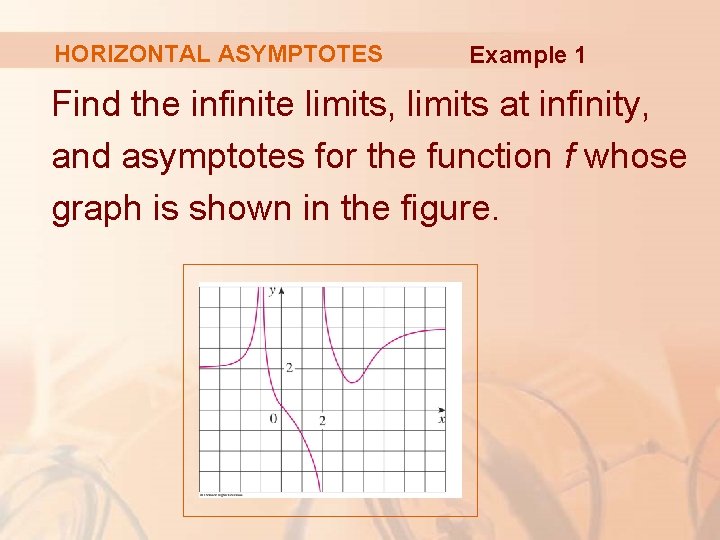
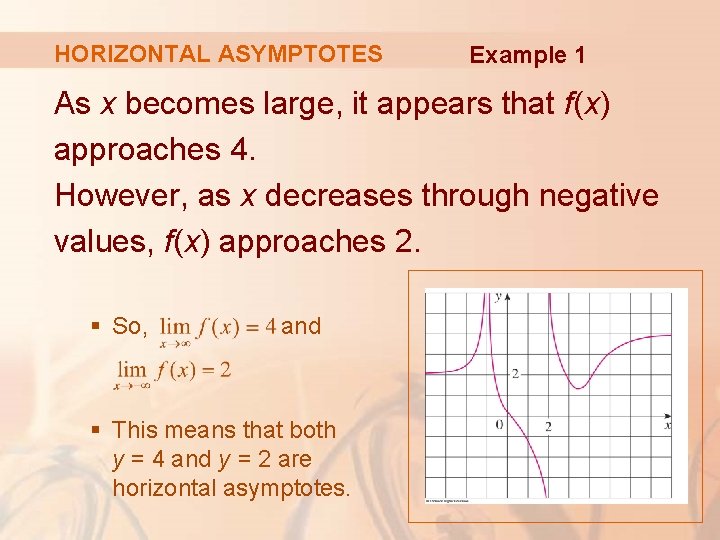
HORIZONTAL ASYMPTOTES Example 1 Find the infinite limits, limits at infinity, and asymptotes for the function f whose graph is shown in the figure.

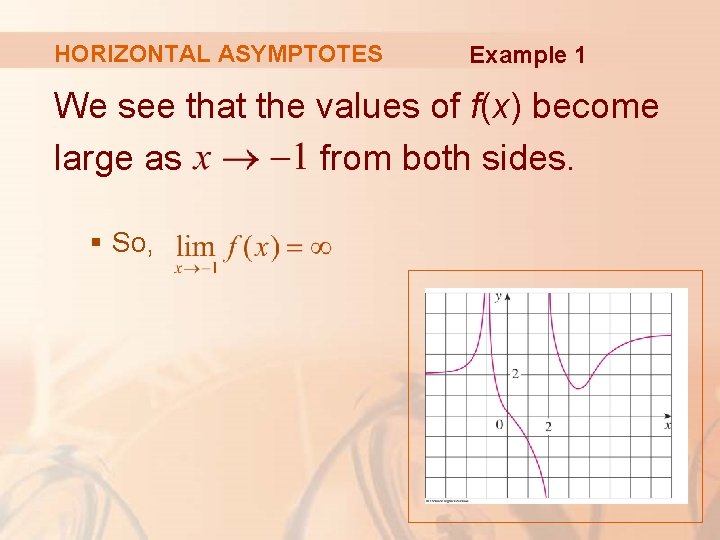
HORIZONTAL ASYMPTOTES Example 1 We see that the values of f(x) become large as from both sides. § So,

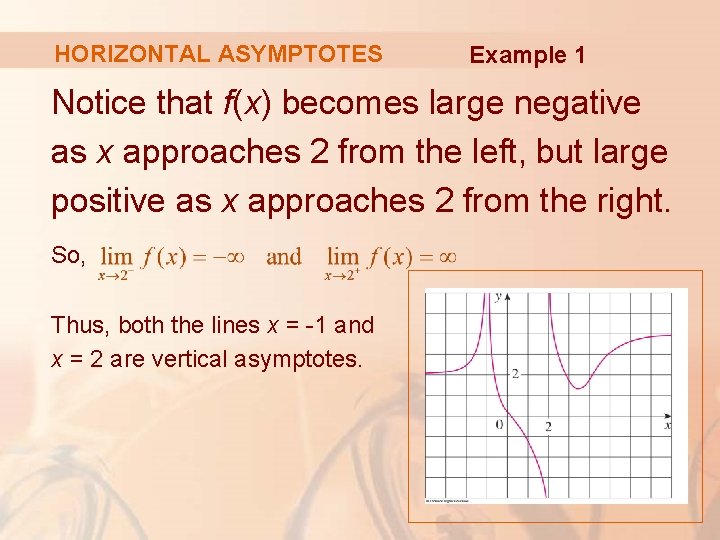
HORIZONTAL ASYMPTOTES Example 1 Notice that f(x) becomes large negative as x approaches 2 from the left, but large positive as x approaches 2 from the right. So, Thus, both the lines x = -1 and x = 2 are vertical asymptotes.

HORIZONTAL ASYMPTOTES Example 1 As x becomes large, it appears that f(x) approaches 4. However, as x decreases through negative values, f(x) approaches 2. § So, and § This means that both y = 4 and y = 2 are horizontal asymptotes.

HORIZONTAL ASYMPTOTES Example 2 Find § Observe that, when x is large, 1/x is small. § For instance, § In fact, by taking x large enough, we can make 1/x as close to 0 as we please. § Therefore, according to Definition 1, we have

HORIZONTAL ASYMPTOTES Example 3 Evaluate and indicate which properties of limits are used at each stage. § As x becomes large, both numerator and denominator become large. § So, it is not obvious what happens to their ratio. § We need to do some preliminary algebra.

HORIZONTAL ASYMPTOTES Example 3 In this case, the highest power of x in the denominator is x 2. So, we have:

HORIZONTAL ASYMPTOTES Example 3

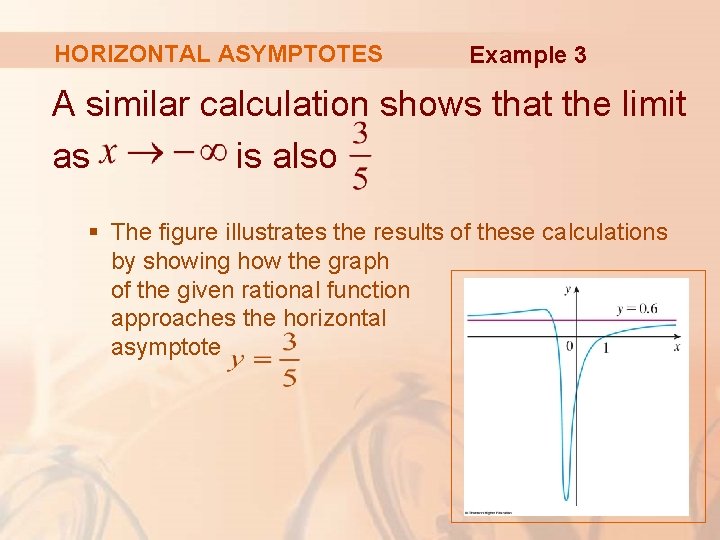
HORIZONTAL ASYMPTOTES Example 3 A similar calculation shows that the limit as is also § The figure illustrates the results of these calculations by showing how the graph of the given rational function approaches the horizontal asymptote

Degree of numerator = degree of denominator , y = 5 x 6 /2 x 6 = 5/2 y = 5/2

Degree of numerator < degree of denominator y = 0 is the horizontal asymptote

HORIZONTAL ASYMPTOTES Example 4 Find the horizontal and vertical asymptotes of the graph of the function

HORIZONTAL ASYMPTOTES Example 4 Dividing both numerator and denominator by x and using the properties of limits, we have:

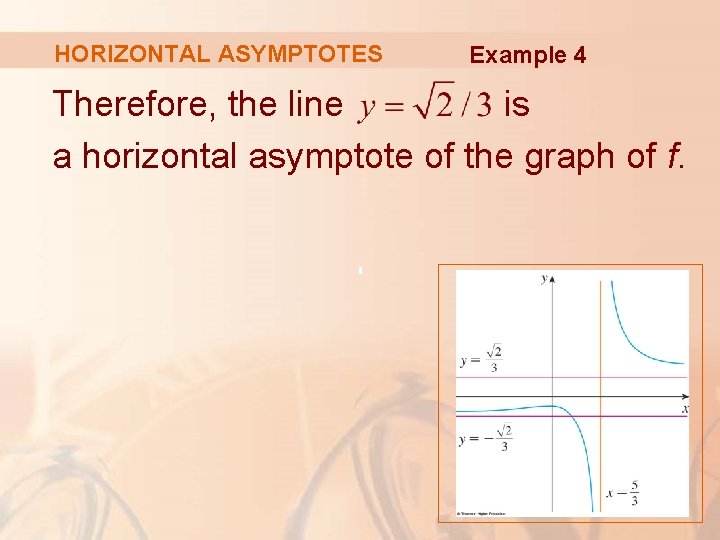
HORIZONTAL ASYMPTOTES Example 4 Therefore, the line is a horizontal asymptote of the graph of f.

HORIZONTAL ASYMPTOTES Example 4 In computing the limit as , we must remember that, for x < 0, we have § So, when we divide the numerator by x, for x < 0, we get § Therefore,

HORIZONTAL ASYMPTOTES Example 4 Thus, the line is also a horizontal asymptote.

HORIZONTAL ASYMPTOTES Example 4 A vertical asymptote is likely to occur when the denominator, 3 x - 5, is 0, that is, when § If x is close to and , then the denominator is close to 0 and 3 x - 5 is positive. § The numerator is always positive, so f(x) is positive. § Therefore,

HORIZONTAL ASYMPTOTES Example 4 § If x is close to but , then 3 x – 5 < 0, so f(x) is large negative. § Thus, § The vertical asymptote is

HORIZONTAL ASYMPTOTES Example 5 Compute § As both and x are large when x is large, it’s difficult to see what happens to their difference. § So, we use algebra to rewrite the function.

HORIZONTAL ASYMPTOTES Example 5 We first multiply the numerator and denominator by the conjugate radical:

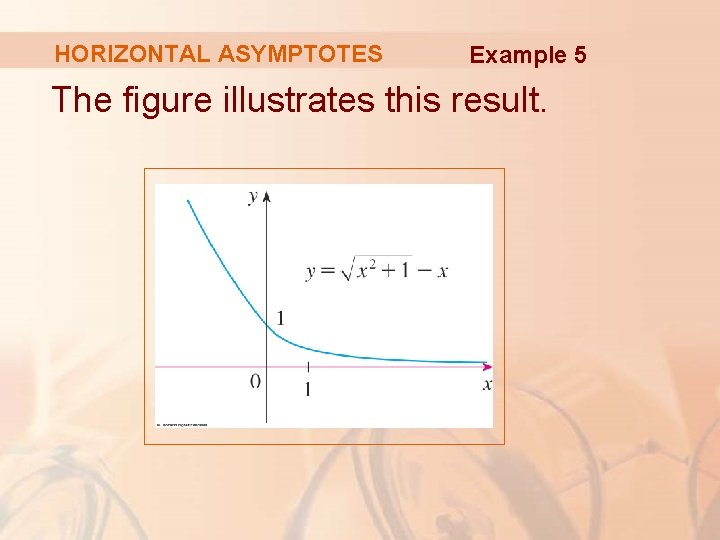
HORIZONTAL ASYMPTOTES Example 5 The figure illustrates this result.

HORIZONTAL ASYMPTOTES Example 6 Evaluate § As x increases, the values of sin x oscillate between 1 and -1 infinitely often. § So, they don’t approach any definite number. § Thus, does not exist.

INFINITE LIMITS AT INFINITY The notation is used to indicate that the values of f(x) become large as x becomes large. § Similar meanings are attached to the following symbols:

INFINITE LIMITS AT INFINITY Find Example 8 and § When x becomes large, x 3 also becomes large. § For instance, § In fact, we can make x 3 as big as we like by taking x large enough. § Therefore, we can write

INFINITE LIMITS AT INFINITY Example 8 § Similarly, when x is large negative, so is x 3. § Thus, § These limit statements can also be seen from the graph of y = x 3 in the figure.

INFINITE LIMITS AT INFINITY Example 9 Find § It would be wrong to write § The Limit Laws can’t be applied to infinite limits because is not a number ( can’t be defined). § However, we can write § This is because both x and x - 1 become arbitrarily large and so their product does too.

INFINITE LIMITS AT INFINITY Example 10 Find § As in Example 3, we divide the numerator and denominator by the highest power of x in the denominator, which is just x: because and as

INFINITE LIMITS AT INFINITY Example 11 Sketch the graph of by finding its intercepts and its limits as and as § The y-intercept is f(0) = (-2)4(1)3(-1) = -16 § The x-intercepts are found by setting y = 0: x = 2, -1, 1.

INFINITE LIMITS AT INFINITY Example 11 Notice that, since (x - 2)4 is positive, the function does not change sign at 2. Thus, the graph does not cross the x-axis at 2. § It crosses the axis at -1 and 1.

INFINITE LIMITS AT INFINITY Example 11 When x is large positive, all three factors are large, so When x is large negative, the first factor is large positive and the second and third factors are both large negative, so
 Limits involving infinity
Limits involving infinity Asymptote rules
Asymptote rules Limits at infinity definition
Limits at infinity definition How to find horizontal asymptotes
How to find horizontal asymptotes Rules for limits to infinity
Rules for limits to infinity Limits involving infinity asymptotes
Limits involving infinity asymptotes Horizontal asymptote
Horizontal asymptote Vertical and horizontal asymptotes limits
Vertical and horizontal asymptotes limits Limits and derivatives class 11
Limits and derivatives class 11 Limits and derivatives
Limits and derivatives Limits and derivatives
Limits and derivatives Real limits statistics
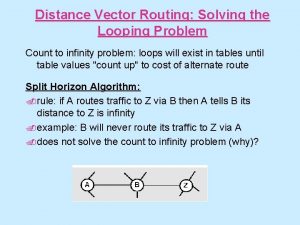
Real limits statistics Count to infinity problem is
Count to infinity problem is Mendel latin america 15m series infinity
Mendel latin america 15m series infinity Activity 3 to infinity and beyond
Activity 3 to infinity and beyond Product and quotient rules and higher order derivatives
Product and quotient rules and higher order derivatives Special trig limits
Special trig limits Hilbert's paradox of the grand hotel
Hilbert's paradox of the grand hotel C3v character table
C3v character table Fungsi numerator
Fungsi numerator Summation math
Summation math How to count past infinity
How to count past infinity Infinity-data.xlsx
Infinity-data.xlsx Infinite geometric sum
Infinite geometric sum Count to infinity problem
Count to infinity problem Count to infinity problem
Count to infinity problem Interval notation for infinity
Interval notation for infinity Complex gsm
Complex gsm Refraction through a rectangular glass slab
Refraction through a rectangular glass slab Tora routing protocol
Tora routing protocol Infinity in greek
Infinity in greek D infinity h point group example
D infinity h point group example Infinity next
Infinity next 1 to infinity
1 to infinity Schoology uplift education
Schoology uplift education Infinity hris
Infinity hris Check point infinity
Check point infinity Hindu cycle of life
Hindu cycle of life Infinity concept
Infinity concept