Limits and continuity Day 1 RATES OF CHANGE





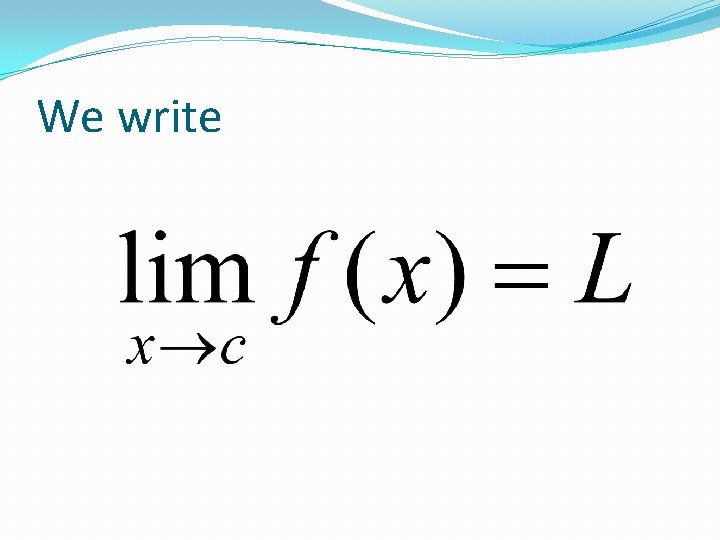
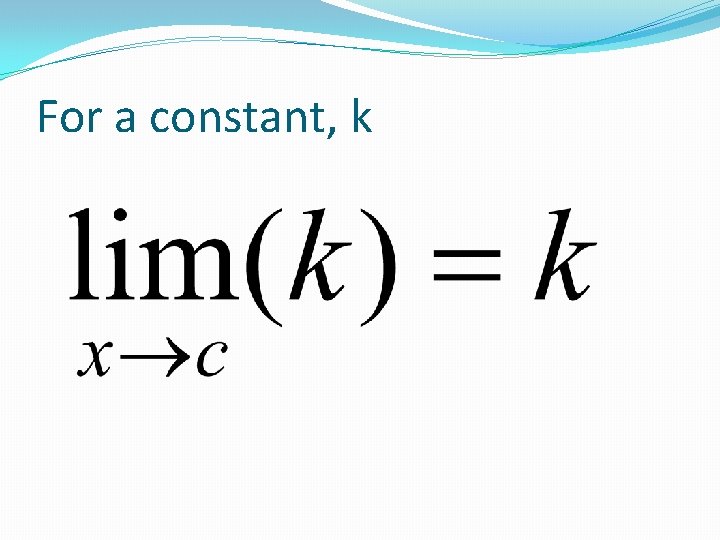














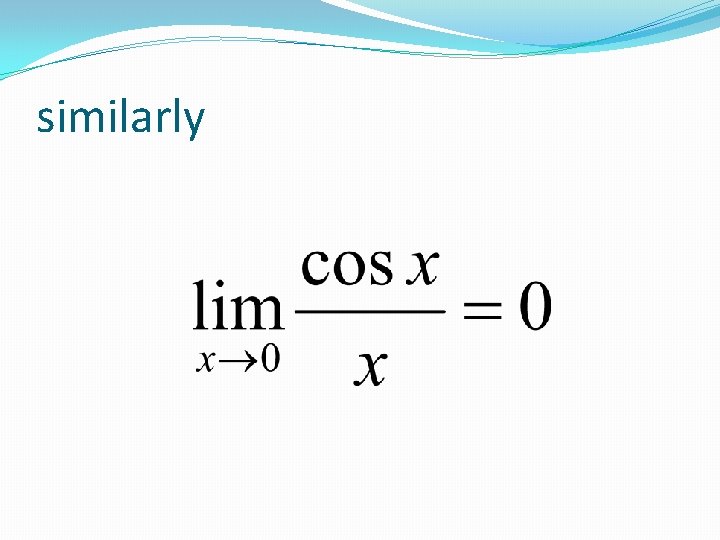










































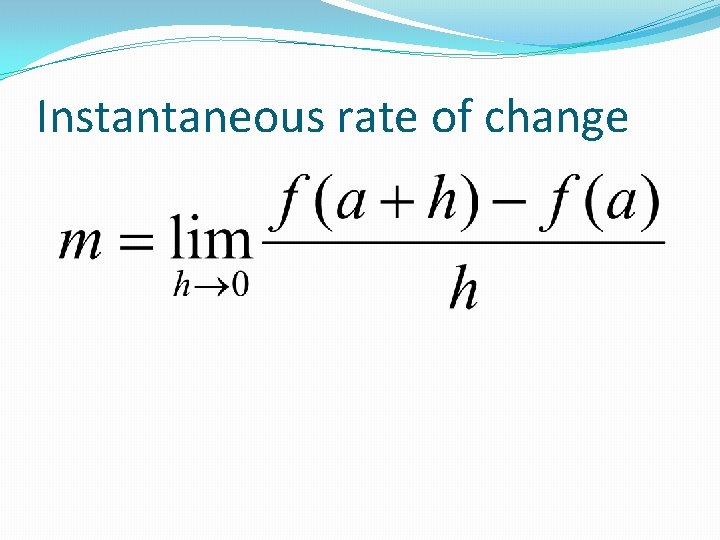




- Slides: 75

Limits and continuity Day 1

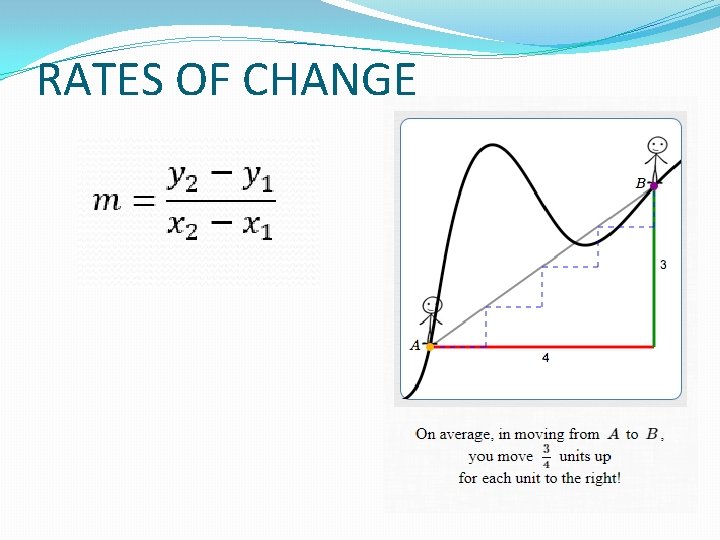
RATES OF CHANGE �If you travel 20 miles in 5 hours, what is your rate of change of distance? �Right! 4 miles per hour �This might lead you to realize that: �Average Speed = distance/time �This is a commonly used rate of change

RATES OF CHANGE

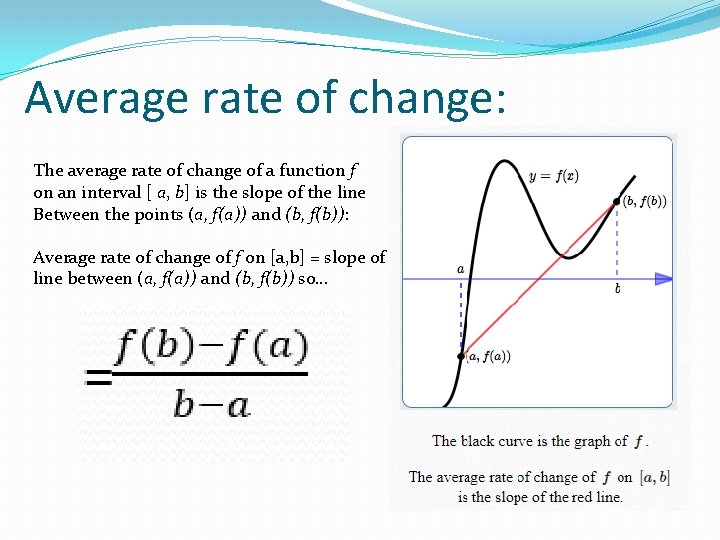
Average rate of change: The average rate of change of a function f on an interval [ a, b] is the slope of the line Between the points (a, f(a)) and (b, f(b)): Average rate of change of f on [a, b] = slope of line between (a, f(a)) and (b, f(b)) so…

Example �

A look at limits �

The basic idea �What we have just looked at is the basic idea of limits as x approaches infinity and negative infinity. �We will look at the formal definition of a limit in this class, but we will not use it. �If you are interested in the formal definition, more information can be found in Appendix 3, page 584
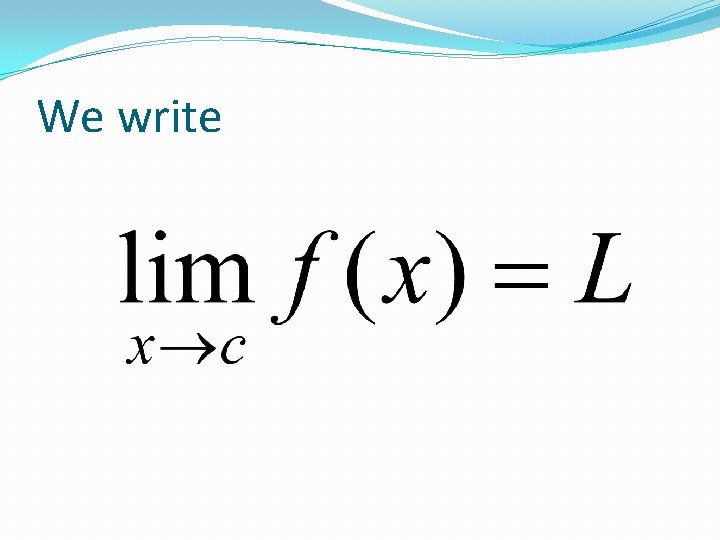
We write
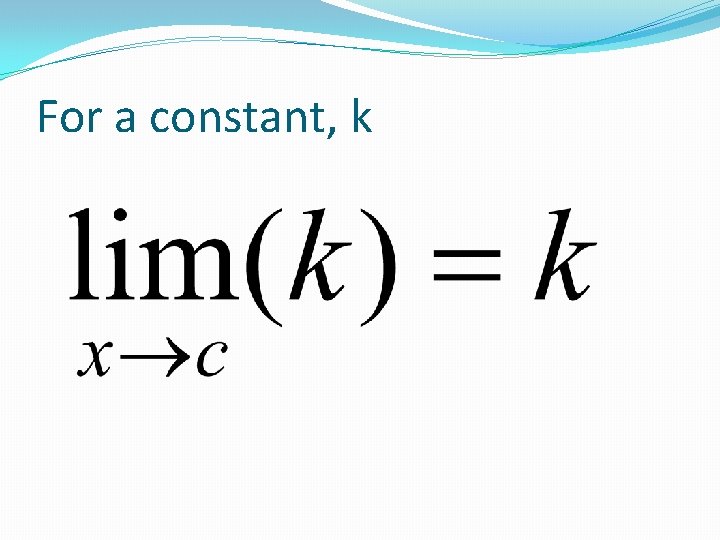
For a constant, k

Limit of the identity function

Properties of Limits

More properties of limits

Limits of rational functions (You learned this before!) �If f(x) and g(x) are polynomials and c is any real number, then if g(c)≠ 0:

One-sided and two-sided limits �Right-hand limit: the limit of f as x approaches c from the right (or the positive side) �Left-hand limit: the limit of f as x approaches c from the left side (or the negative side)

Recall: � What is the limit of a function if the left-hand right-hand limits are different? � No limit

Practice – Pg. 62 #22 �

Practice – Pg. 62 #22 Since graphing will give us an estimate, we can check algebraically. *Remember to factor and simplify before substituting*

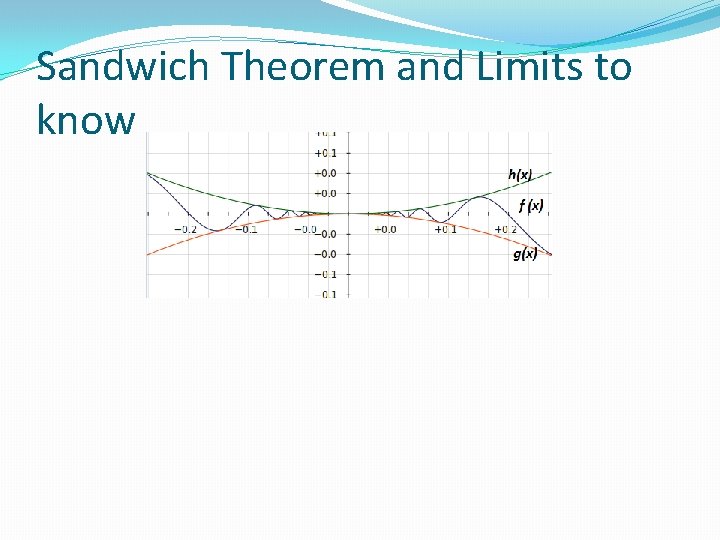
Sandwich Theorem and Limits to know �

Sandwich Theorem and Limits to know

Sandwich Theorem and Limits to know �

Sandwich Theorem and Limits to know �

Sandwich Theorem and Limits to know �Let’s begin with a handout about a limit that you will have to memorize for the AP Test �

Sandwich Theorem Handout

So, memorize
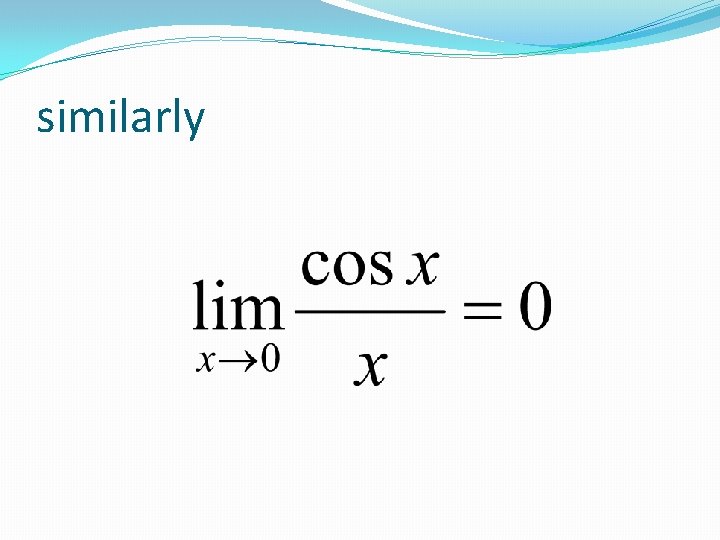
similarly

Which leads us to the Sandwich Theorem �If g(x)≤f(x)≤h(x) for all x≠c in some interval about c, and

Another example � Let’s look at example 9 on page 61 as another example

Page 61 example 9

Practice Let’s do page 64 #53 together. Find the limit graphically then use the sandwich theorem to confirm.

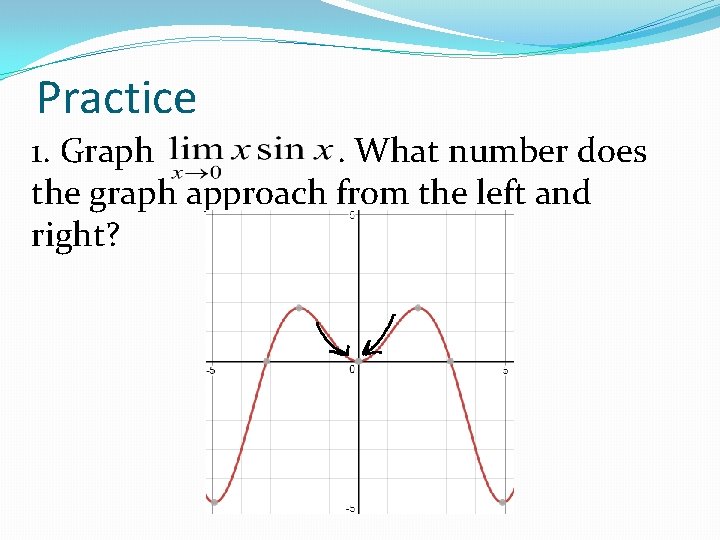
Practice 1. Graph. What number does the graph approach from the left and right?

Practice �

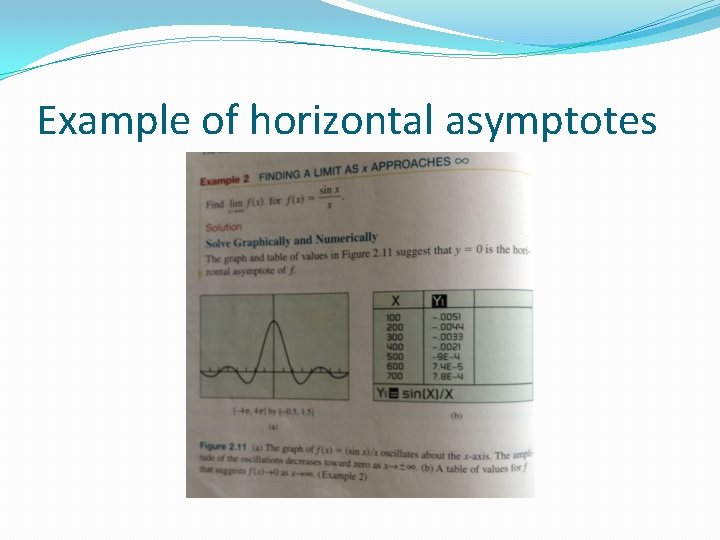
Limits involving infinity ( You may not know this, but you have done these before IN ALG II) �The line y=b is a horizontal asymptote of the graph of a function y=f(x) if either

Example of horizontal asymptotes

Vertical asymptotes �The line x=a is a vertical asymptote of the graph of a function y=f(x) if either:

Example of vertical asymptotes

End behavior model �An end behavior model has the same behaviors as a function as x moves toward ∞ or -∞ �To find one, think of what dominates as the inputs get larger and larger �Let’s examine together examples 7 and 8 on page 70

End Behavior

End behavior

Practice � Let’s do together 71(2, 4, 17, 26, 32, 34, 40)

Practice �

Practice �

Practice �

Practice �

Practice �

Practice �

Practice �

Work day � Quick Quiz 2. 1 -2. 2 � Continuity packet �Together in class

Continuity � Informally – continuity is when you can start at one end of the graph and draw the entire graph without ever having to lift your pencil

Continuity at a Point �Interior Point: A function y=f(x) is continuous at an interior point c of its domain if Endpoint: A function y=f(x) is continuous at a left endpoint a or a right endpoint b of its domain if:

Examples of continuous functions �Polynomials �Sine �Cosine �Exponential �Logarithmic �Radical �Algebraic combinations of continuous functions (where defined) �Composites of continuous functions*

Discontinuity � If a function is not continuous at a point c, we say that f is discontinuous at c, and c is a point of discontinuity of f.

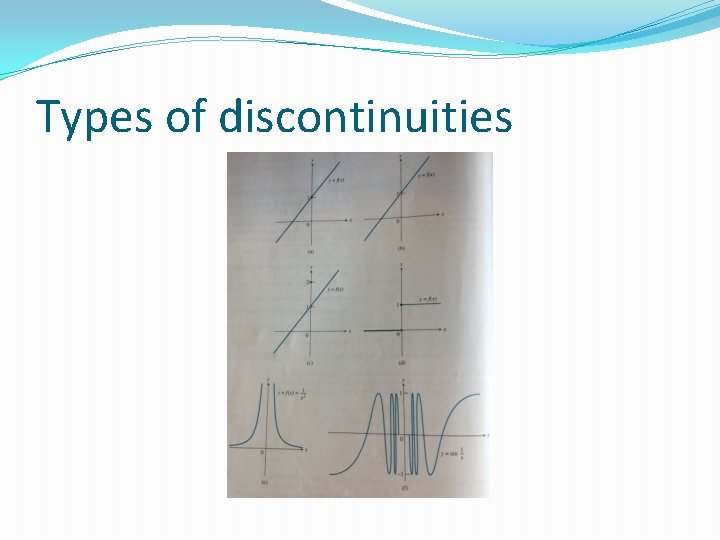
Types of discontinuities � Removable (this is a “hole”) � Jump � Infinite (like a vertical asymptote) � Oscillating

Types of discontinuities

Exploration 1 � Take a few minutes to complete page 77 Exploration 1. � Take note of what an “extended function” is

Exploration 1

Is any real number exactly 1 less than its cube? �We answer this question by applying the Intermediate Value Theorem in the following way. Any such number must satisfy the equation x=x 3 -1 or, equivalently, x 3 -x-1=0. Hence, we are looking for a zero value of the continuous function f(x)=x 3 -x-1. The function changes signs between 1 and 2, so there must be a point c between 1 and 2 where f(c)=0.

Practice �

Practice �

Practice �

Practice �

Practice �

Practice �

Practice #24 – Open your books (pg. 81) a) Find each point of discontinuity b) Which of the discontinuity are removable? Not removable? Give reasons.

Practice �

Average rate of change �Average rate of change = quantity of change divided by the time for the change. �Note: This is the slope of the secant line through the beginning and ending points of the time interval.

Instantaneous rate of change �Instantaneous rate of change is the slope of the tangent line. �Note: The tangent line can be found by making secants over smaller and smaller time intervals.

Slope of a curve at a point � The slope of a curve at a point is defined to be the slope of the tangent line at that point. � Note: This is a BIG idea

Slope of a curve �The slope of a curve at a point P(a, f(a)), if it exists is

The difference quotient

Normal line �The normal line to a curve at a point is the line perpendicular to the tangent at that point. �Recall, the slope of a perpendicular line is the opposite reciprocal of the slope of the line.
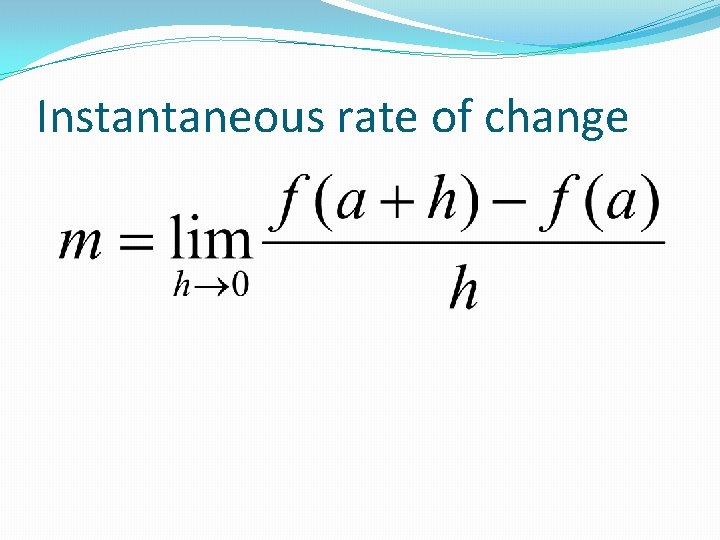
Instantaneous rate of change

Practice �

Practice �

Homework Review 2. 1 & 2. 2 Quiz Assign 2. 3 & 2. 4 Quick Quiz

Homework �Pg. 62(1 -6, 9, 15, 17, 18, 21, 24, 25, 31, 33) �Pg. 62(39, 42, 43, 46, 49, 51, 54, 58 a, b) �Pg. 71(3 -48 multiples of 3 (omit 45), 54, 57, 59) �Pg. 80(1 -29 odd, 36, 39, 42, 48) �Pg. 87(1 -33 odd) �Pg. 91(1, 5, 7, 13, 15 -20, 29, 31, 32, 35, 37, 39, 43, 47, 49)