Limit Definition of the Derivative Objective To use

Limit Definition of the Derivative

Objective Ø To use the limit definition to find the derivative of a function. Ø TS: Devoloping a capacity for working within ambiguity.

Slope Ø Slope: the rate at which a line rises or falls Ø For a line, the rate (or slope) is the same at every point on the line. Ø For graphs other than lines, the rate at which the graph rises or falls changes from point to point.

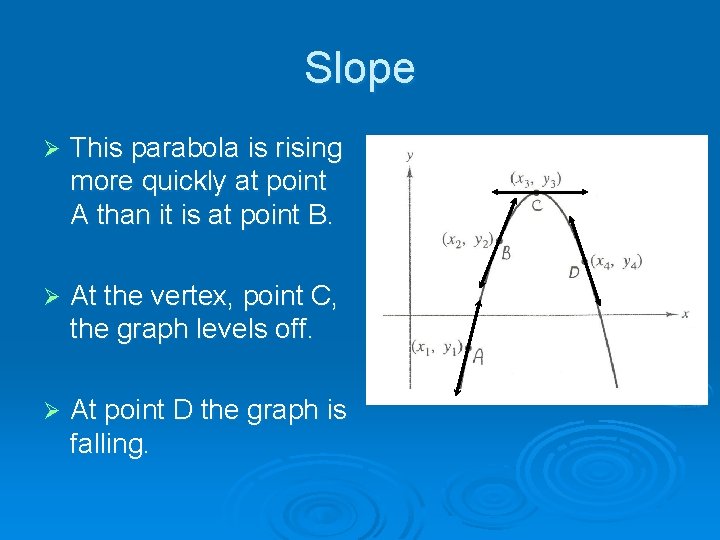
Slope Ø This parabola is rising more quickly at point A than it is at point B. Ø At the vertex, point C, the graph levels off. Ø At point D the graph is falling.

Slope Ø To determine the rate at which a graph rises or falls at a single point, we can find the slope of the tangent line to the point. Ø How do we calculate the slope of a tangent line?

Video Clip from Calculus-Help. com The Difference Quotient

The Difference Quotient Ø The derivative is the slope of the tangent line to a graph f(x), and is usually denoted f’(x). Ø To calculate the slope of the tangent line we will use the difference quotient.

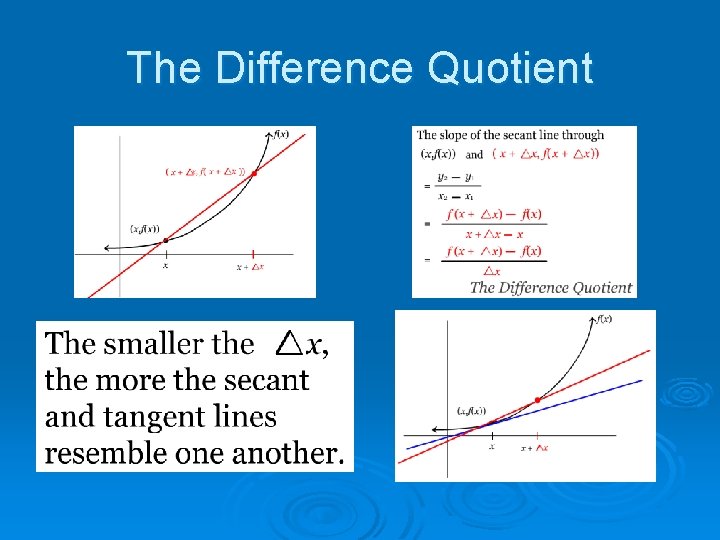
The Difference Quotient

Limit Definition of the Derivative The derivative is the formula which gives the slope of the tangent line at any point x for f (x), and is denoted provided this limit exists.

Derivatives Ø The derivative of the function y = f (x) may be expressed as … “f prime of x” Prime notation “y prime” Leibniz notation “the derivative of y with respect to x”

Derivatives Ø The process of finding derivatives is called differentiation. Ø A function is differentiable at a point if its derivative exists at that point.

Limit Definition of the Derivative Ø Use the limit definition to find the derivative of:

Limit Definition of the Derivative

Limit Definition of the Derivative A formula for finding the slope of the tangent line of f (x) at a given point.

Limit Definition of the Derivative Ø Use the limit definition to find the derivative of:

Limit Definition of the Derivative

Limit Definition of the Derivative A formula for finding the slope of the tangent line of f (x) at a given point.

Differentiability Ø Not every function is differentiable at all points. Ø Some common situations in which a function will not be differentiable at a point include: 1. Vertical tangent lines 2. Discontinuities (like a hole, break, or vertical asymptote) 3. Sharp turns (called cusps & nodes)

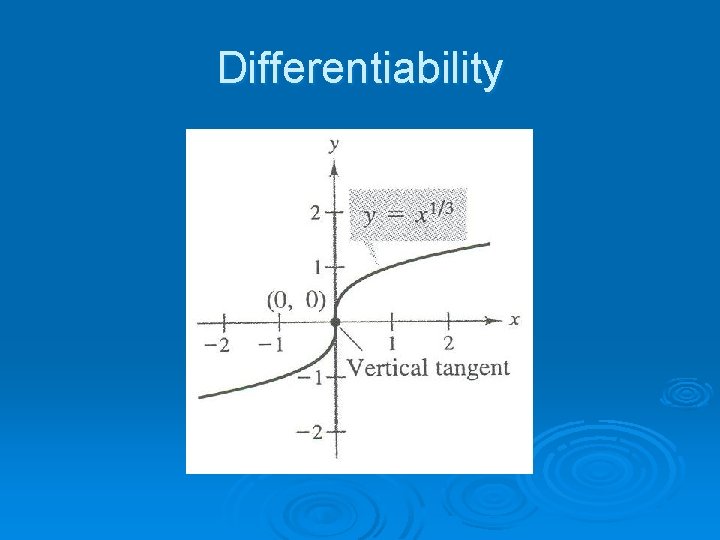
Differentiability

Differentiability

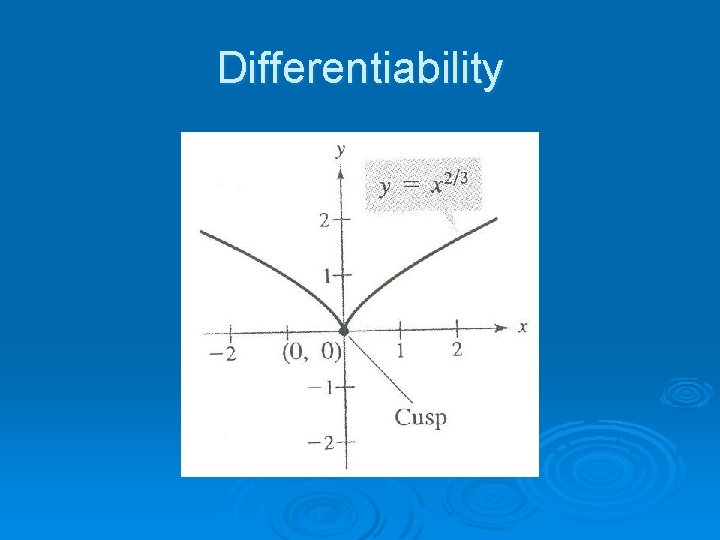
Differentiability

Differentiability

CALCULUS JEOPARDY! $200 Answer: It’s computed by finding the limit of the difference quotient as ∆x approaches 0. Question: What is the derivative?

CALCULUS JEOPARDY! $400 Answer: It’s used to find the slope of a function at a point. Question: What is the derivative?

CALCULUS JEOPARDY! $600 Answer: It’s used to find the slope of the tangent line to a graph f (x), and is usually denoted f’(x). Question: What is the derivative?

CALCULUS JEOPARDY! $800 Answer: It’s used to find the instantaneous rate of change of a function. Question: What is the derivative?

CALCULUS JEOPARDY! $1000 Answer: It’s the thing we love most about calculus. Question: What is the derivative?

The Derivative is… Ø computed by finding the limit of the difference quotient as ∆x approaches 0. Ø the slope of a function at a point. Ø the slope of the tangent line to a graph f (x), and is usually denoted f’(x). Ø the instantaneous rate of change of a function.