Liikumine Liikumine Kinemaatika tuleneb kreekakeelsest snast kinema mis

Liikumine

Liikumine "Kinemaatika" tuleneb kreekakeelsest sõnast kinema, mis tähendab liikumist. Vastav mehaanika osa uuribki liikumist - mitte niivõrd selle põhjusi kui just liikumise matemaatilise kirjeldamise võimalusi. Liikumine on looduse põhiomadusi. Seisvaid asju pole olemas. Paigalseis on alati suhteline (liikumatus millegi/kellegi suhtes). Liikumist ennast on kahte tüüpi: • kulgev liikumine, kui vabalt liigutatav keha muudab oma asukohta (toas, tänaval) ja • pöörlev liikumine, kui keha on kinnitatud (pöörlemisteljele) ja võib seetõttu vaid pöörduda, muutes oma ruumilist orientatsiooni (asendit ruumis, püsti, külili, kummuli). Liikumine tähendab asukoha ning asendi (orientatsiooni) muutumist. Muutumine nõuab vähemalt kaht parameetrit, millest üks väljendab liikumist ennast on teine aga argumendiks (muutub sõltumatult liikuvast kehast). Selleks sõltumatuks argumendiks aeg.

Liikumise suhtelisus: Galilei relatiivsusprintsiip Katseliselt tuvastatavat absoluutset liikumist pole olemas. Paigalseis ja liikumine on suhtelised mõisted ning sõltuvad vaatleja liikumisest. Keha liikumise trajektoor ja kiirus sõltuvad taustsüsteemi valikust. Taustsüsteem on mingi kehaga seotud ruumiliste ja ajaliste koordinaatide süsteem. Taustsüsteemi nimetame inertsiaalseks, kui kõik vabad kehad liiguvad temas ühtlaselt ja sirgjooneliselt ruum on ühtlane, isotroopne ja aeg on ühesugune. Inertsiaalsüsteeme, mis liiguvad üksteise suhtes ühtlaselt ja sirgjooneliselt on lõpmatu hulk. Kõik nad on samaväärsed (neis kõigis toimivad füüsikaseadused ühtemoodi) Mitteinertsiaalne süsteem liigub inertsiaalsete suhtes kiirendusega.

Keha asendi ja selle muutuste/nihke kvantitatiivseks kirjeldamiseks kasutatakse ruumikoordinaate. Koordinaadid on arvud, mis määravad keha kauguse mingitest kindlaksmääratud kohtadest - koordinaat-telgedest. Kolmemõõtmelises ruumis (ainuke inimese poolt tunnetatav) on asendi määramiseks vaja kolme arvu (koordinaati), kahemõõtmelises (tasapinnal) kaks ja ühemõõtmelises (joonel) üksainus arv. Need koordinaadid koos koordinaattelgede alguspunktiga moodustavad asukoha raadiusvektori (sirge, mis algab 0 ja lõpeb antud punktis). Teepikkus s (ehk nihkevektor) on vektor, millel on x, y, ja z- suunalised komponendid

Koordinaadid peavad olema üksteisest Koordinaadid sõltumatud • Koordinaadid on arvud, mis määravad keha kauguse mingitest kindlaksmääratud kohtadest - koordinaattelgedest • Koordinaadid peavad olema üksteisest sõltumatud • Teine moodus seda öelda on, koordinaadid asetsevad omavahel risti • Kolmas, et nad on ortogonaalsed A = Axx+Ayy+Azz • Ortogonaalsuse vajalik ja piisav tingimus: piisav tingimus Teljevektorite skalaarkorrutis=0 • Liikumised sõltumatute koordinaatide suunas on teineteisest sõltumatud kus An – vektori projektsioonid telgedele

Liikumise trajektoor, kiirus ja kiirendus Liikumist iseloomustavad trajektoor, kiirus ja kiirendus. Erinevatel ajahetkedel saadud asukoha (koordinatide) üleskirjutus on keha trajektoor. Trajektoor koosneb diskreetsetest punktidest. Trajektoori matemaatilisel üldistusel saame pideva liikumisvõrrandi näiteks kujul s = s(t). A(t) = Ax(t)x+Ay(t)y+Az(t)z Liikumisvõrrandi esimest tuletist aja järgi nimetatakse kiiruseks. Kiirus (v) on füüsikaline suurus, mida mõõdetakse ajaühikus läbitud teepikkusega. Kiiruse hetkväärtust arvutatakse kui Liikumisvõrrandi teist tuletist aja järgi (kiiruse esimest tuletist) nimetatakse kiirenduseks. Ebaühtlase liikumise kiirendus (a) on füüsikaline suurus, mida mõõdetakse kiiruse muutusega ajaühikus.
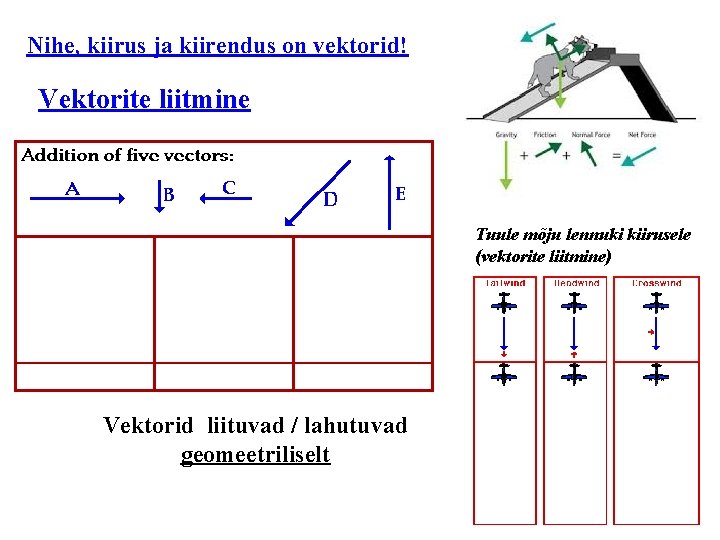
Nihe, kiirus ja kiirendus on vektorid! Vektorite liitmine Tuule mõju lennuki kiirusele (vektorite liitmine) Vektorid liituvad / lahutuvad geomeetriliselt
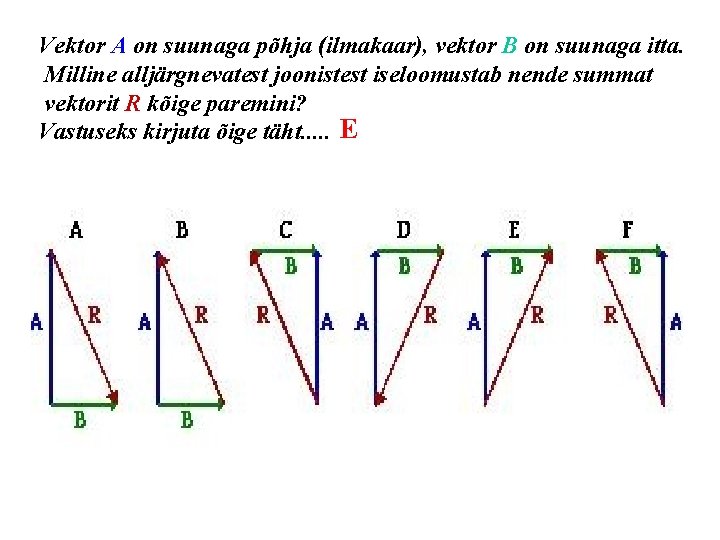
Vektor A on suunaga põhja (ilmakaar), vektor B on suunaga itta. Milline alljärgnevatest joonistest iseloomustab nende summat vektorit R kõige paremini? Vastuseks kirjuta õige täht. . . E
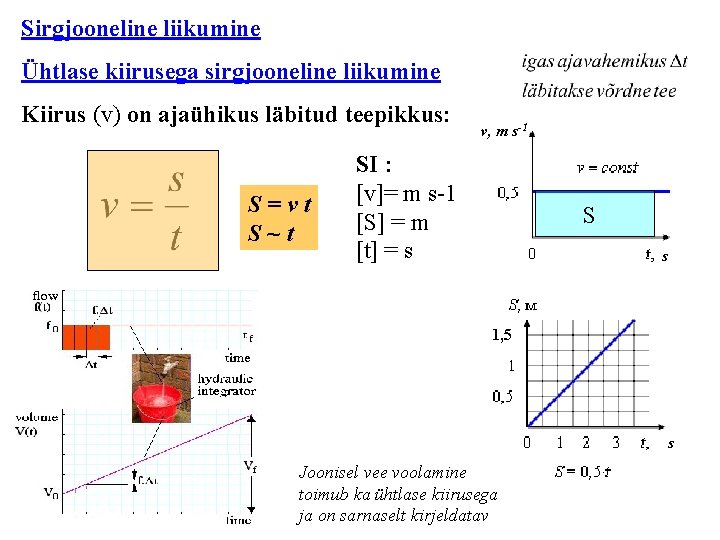
Sirgjooneline liikumine Ühtlase kiirusega sirgjooneline liikumine Kiirus (v) on ajaühikus läbitud teepikkus: S=vt S~t v, m s-1 SI : [v]= m s-1 [S] = m [t] = s S s 1, 5 s Joonisel vee voolamine toimub ka ühtlase kiirusega ja on sarnaselt kirjeldatav

Liikumise graafiline esitus Ühtlase kiirusega liikumine positiivses suunas

Liikumise graafiline esitus Ühtlase kiirusega liikumine negatiivses suunas S < 0, v < 0

Kirjeldage kehade 1 ja 2 liikumist - ajahetkel 0 mõlemad kehad alustavad liikumist positiivses suunas - keha 1 alustab liikumist olles 1 m võrra ees kehast 2 - läbitud teepikkus on võrdeline ajaga, seega liikumine on ühtlase kiirusega S, m s - sirgete tõusud on võrdsed, ehk liikumiskiirused v 1 = v 2 - kehad läbivad 1 meetri 2 sekundi jooksul, siit v 1 = v 2 = 0. 5 m/s
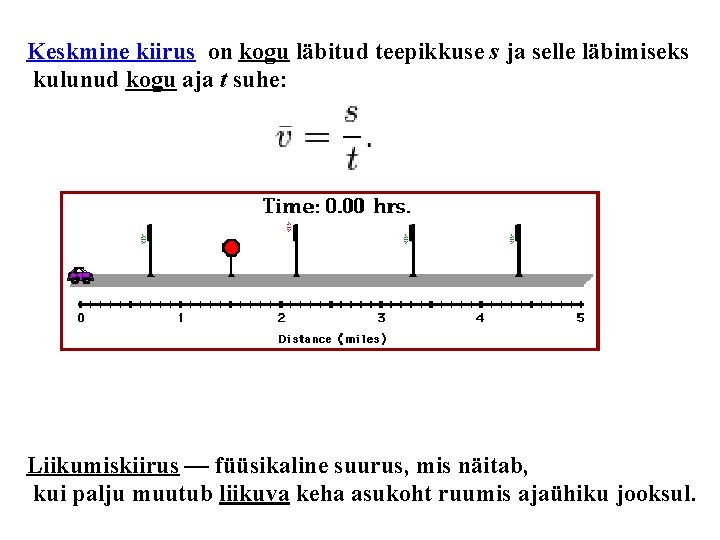
Keskmine kiirus on kogu läbitud teepikkuse s ja selle läbimiseks kulunud kogu aja t suhe: Liikumiskiirus — füüsikaline suurus, mis näitab, kui palju muutub liikuva keha asukoht ruumis ajaühiku jooksul.

Auto sõitis Tallinnast Tartusse, vahemaa oli 200 km. Esimese 100 km vältel oli kiirus 50 km h-1, siis aga 100 km h-1. Missugune oli keskmine kiirus? Kui kiirus oleks olnud ühtlane, siis oleks asi lihtne: v = s : t. Ebaühtlase kiiruse puhul aga tuleb kõigepealt leida teel oldud aeg: t = 100/50 + 100/100 = 2 + 1 = 3 h ja alles siis same läbitud tee pikkuse kaudu arvutada keskmise kiiruse: v = 200/3 = 66. 67 km/h. Kiirus ei keskmistu mitte läbitud teepikkuse, vaid teel oldud aja kaudu. Keskmine kiirus:

Ülesande tingimustest teate: - läbitud teepikkus oli 200 km, - 1 -100 km kiirus oli 50 km/h, - 100 -200 km kiirus oli 100 km/h - kui a = 0 S kasvab lineaarselt ja kiirus = const Ülesande lahendusest teate: - sõit võttis aega kokku 3 h, - 1 -100 km sõideti 2 h, - 100 -200 km sõideti 1 h Kandke graafikule alg- ja lõpppunktid ja ühendage nad vastavate kõveratega/sirgetega. Punase sirge tõus teepikkuse graafikul ongi keskmine kiirus

Ebaühtlane liikumine
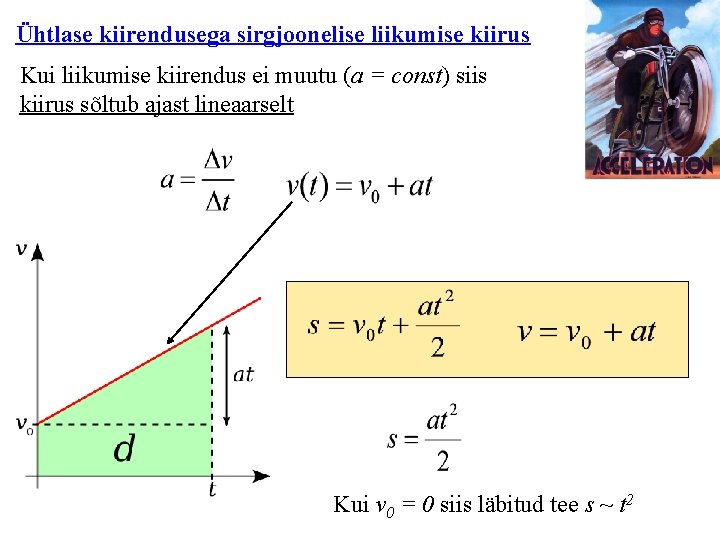
Ühtlase kiirendusega sirgjoonelise liikumise kiirus Kui liikumise kiirendus ei muutu (a = const) siis kiirus sõltub ajast lineaarselt Kui v 0 = 0 siis läbitud tee s ~ t 2

Liikumise graafiline esitus Kiirendus positiivses suunas

Liikumise graafiline esitus Kiirendus negatiivses suunas Algkiirus on 0 ja kiirus läheb negatiivsemaks (väheneb), siit a<0
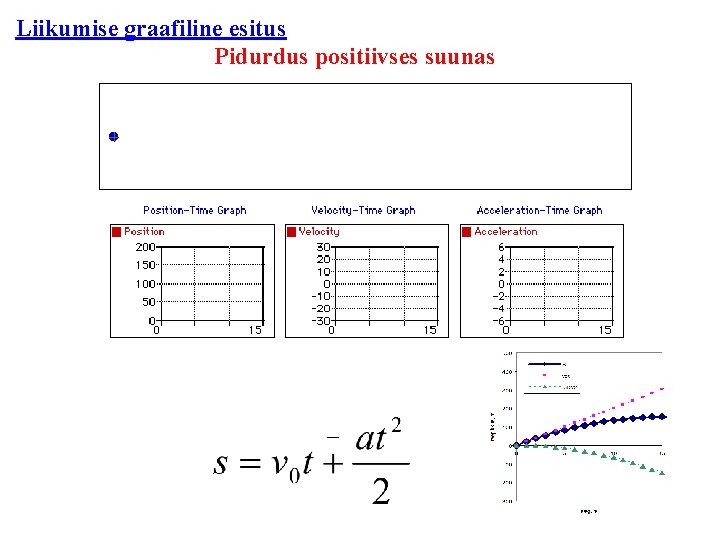
Liikumise graafiline esitus Pidurdus positiivses suunas _

Liikumise graafiline esitus Pidurdus negatiivses suunas V < 0 ja läheb positiivsemaks (kasvab), siit a>0

Joonisel on esitatud sõiduki liikumise kiiruse muutus ajas. Arvutage sõiduki kiirendus kolmandal sekundil. Graafikul on keha kiiruse sõltuvus ajast. Kirjeldage keha liikumist. Graafikul on keha kiirenduse sõltuvus ajast. Millisel ajahetkel sõiduki kiirus on kõige suurem?

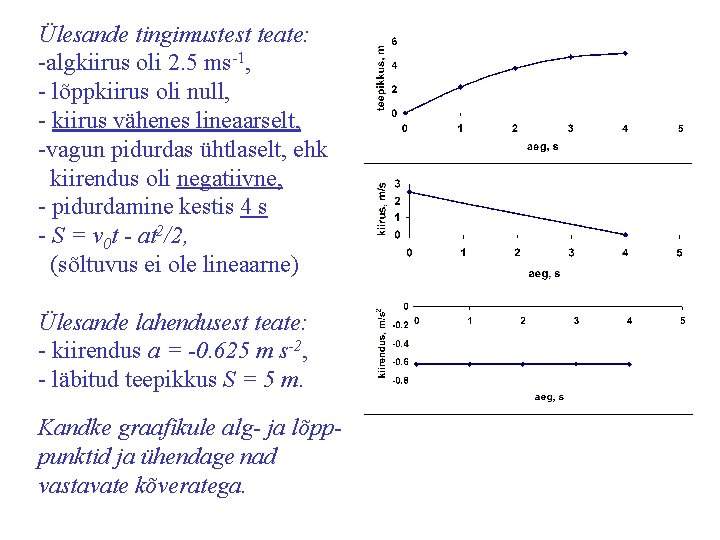
Ülesande tingimustest teate: -algkiirus oli 2. 5 ms-1, - lõppkiirus oli null, - kiirus vähenes lineaarselt, -vagun pidurdas ühtlaselt, ehk kiirendus oli negatiivne, - pidurdamine kestis 4 s - S = v 0 t - at 2/2, (sõltuvus ei ole lineaarne) Ülesande lahendusest teate: - kiirendus a = -0. 625 m s-2, - läbitud teepikkus S = 5 m. Kandke graafikule alg- ja lõpppunktid ja ühendage nad vastavate kõveratega.
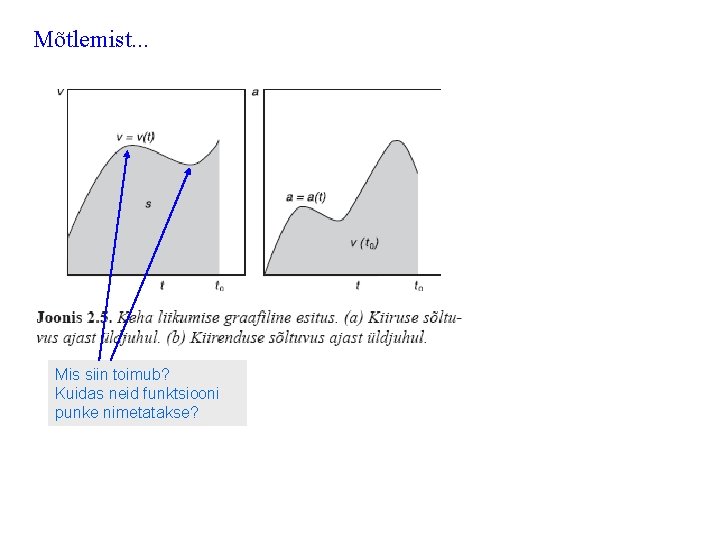
Mõtlemist. . . Mis siin toimub? Kuidas neid funktsiooni punke nimetatakse?

Vaba langemine g = 9. 8 ms-2
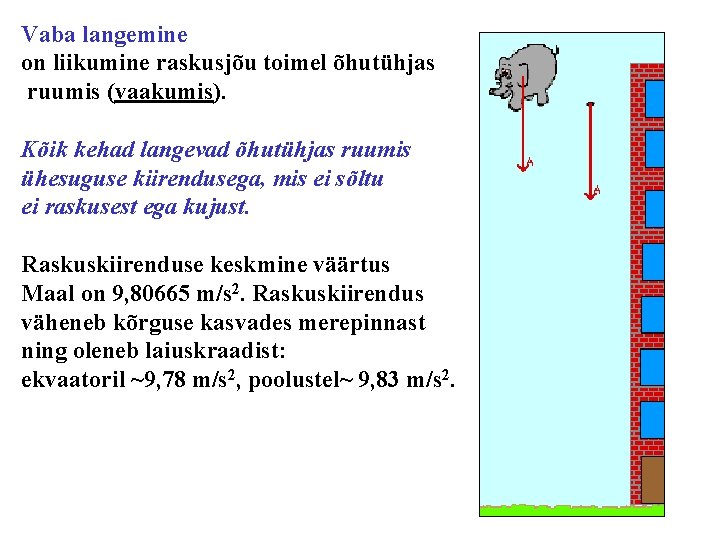
Vaba langemine on liikumine raskusjõu toimel õhutühjas ruumis (vaakumis). Kõik kehad langevad õhutühjas ruumis ühesuguse kiirendusega, mis ei sõltu ei raskusest ega kujust. Raskuskiirenduse keskmine väärtus Maal on 9, 80665 m/s 2. Raskuskiirendus väheneb kõrguse kasvades merepinnast ning oleneb laiuskraadist: ekvaatoril ~9, 78 m/s 2, poolustel~ 9, 83 m/s 2.
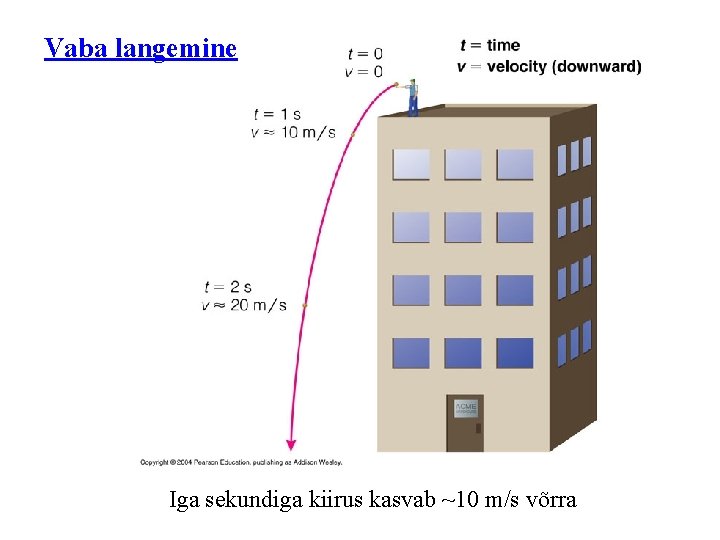
Vaba langemine Iga sekundiga kiirus kasvab ~10 m/s võrra

Langemine + horisontaalliikumine Vaba langemise aeg ei sõltu sellest, kas keha võtab osa ka horisontaalliikumisest. Langemise aeg sõltub ainult keha asukoha kõrgusest maapinnalt (õhutakistust ei arvesta).

Vaba langemise aeg sõltub ainult raskuskiirendusest (g) ja keha algkõrgusest maapinnalt




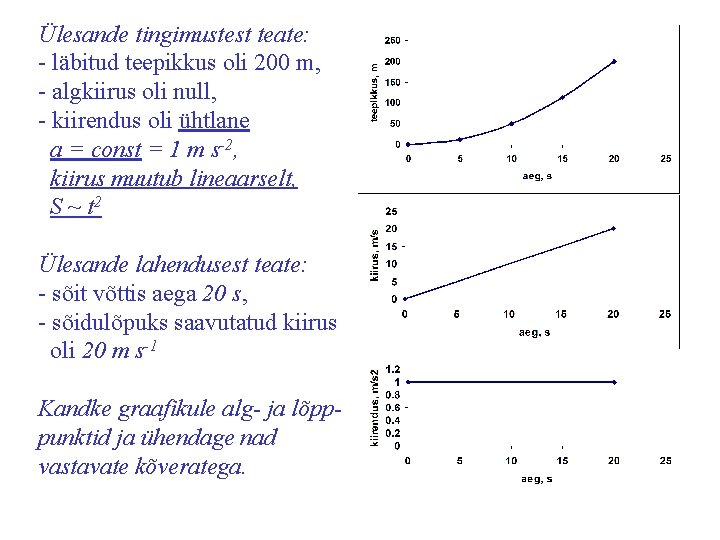
Ülesande tingimustest teate: - läbitud teepikkus oli 200 m, - algkiirus oli null, - kiirendus oli ühtlane a = const = 1 m s-2, kiirus muutub lineaarselt, S ~ t 2 Ülesande lahendusest teate: - sõit võttis aega 20 s, - sõidulõpuks saavutatud kiirus oli 20 m s-1 Kandke graafikule alg- ja lõpppunktid ja ühendage nad vastavate kõveratega.

Soovin edu !
- Slides: 36