Light Pulse Atom Interferometry for Precision Measurement Jaewan

Light Pulse Atom Interferometry for Precision Measurement Jaewan Kim Myongji University

AI for Precision Measurements • Inertial Sensing – Gravimeters, Gyroscopes, Gradiometers • Newton’s constant G • Fine-structure constant and h/M • Test of Relativity • Interferometers in space • …

Gravity Measurements Geophysics Gravity field mapping (crustal deformations, mass changes, definition of the geoid …) Navigation (submarine…) Tests of fundamental physics (equivalence principle, tests of gravitation …) Metrology: Watt Balance (new definition of the kg) g

Absolute Gravimeters Commercial Gravimeter : FG 5 Principle : Michelson interferometer with falling corner cube Accuracy : 2 µGal 1 µGal = 10 -8 m/s 2 ~ 10 -9 g Atomic gravimeter Stanford experiment in 2001 : – Resolution: 3 µGal after 1 minute – Accuracy: <3 µGal From A. Peters, K. Y. Chung and S. Chu

Principle of Atom Interferometry

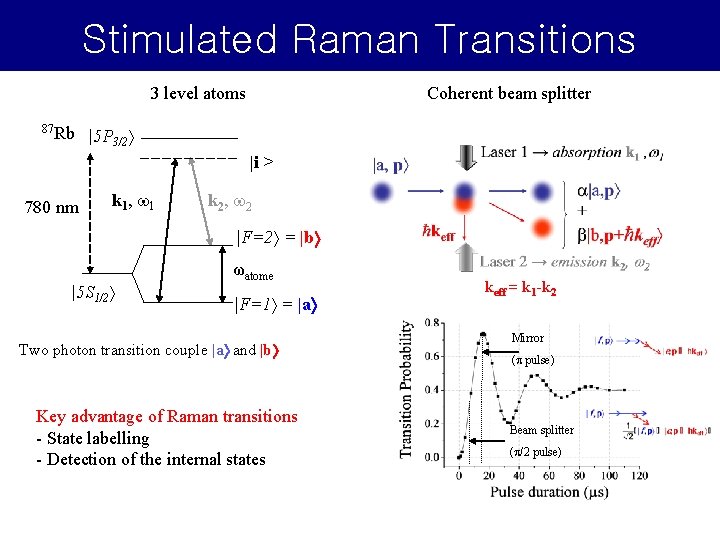
Stimulated Raman Transitions Coherent beam splitter 3 level atoms 87 Rb |5 P 3/2 |i > 780 nm k 1 , 1 k 2 , 2 |F=2 = |b |5 S 1/2 ωatome |F=1 = |a Two photon transition couple |a and |b Key advantage of Raman transitions - State labelling - Detection of the internal states keff = k 1 -k 2 Mirror (p pulse) Beam splitter (p/2 pulse)

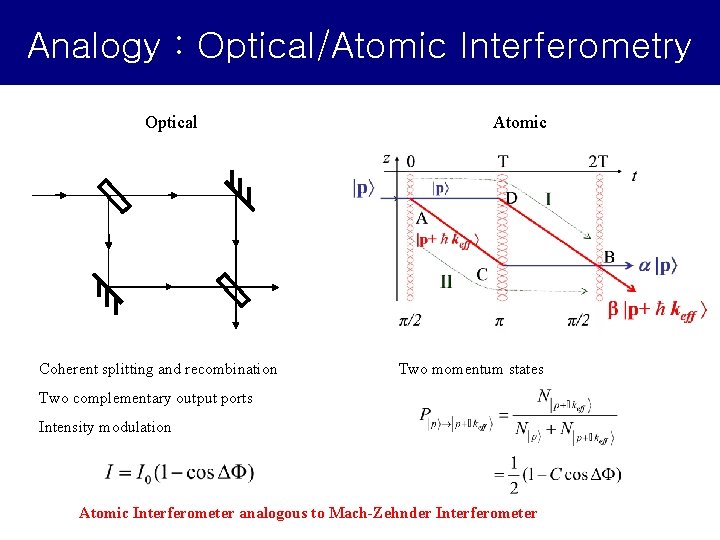
Analogy : Optical/Atomic Interferometry Optical Coherent splitting and recombination Atomic Two momentum states Two complementary output ports Intensity modulation Atomic Interferometer analogous to Mach-Zehnder Interferometer

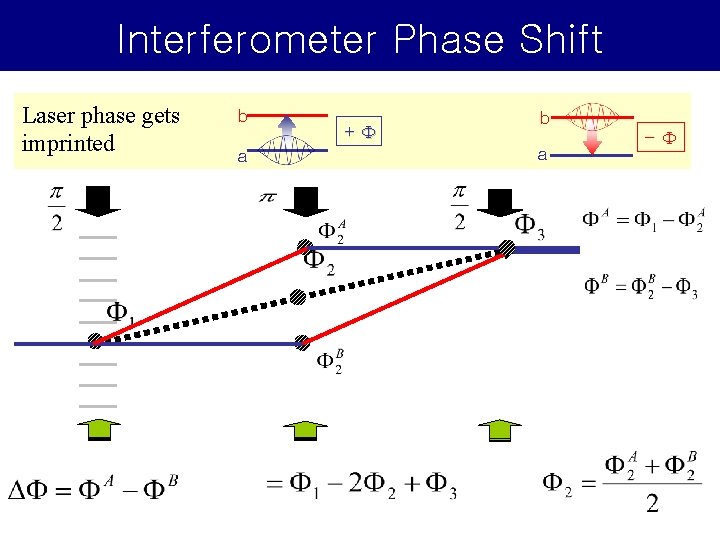
Interferometer Phase Shift Laser phase gets imprinted b a +F b a -F

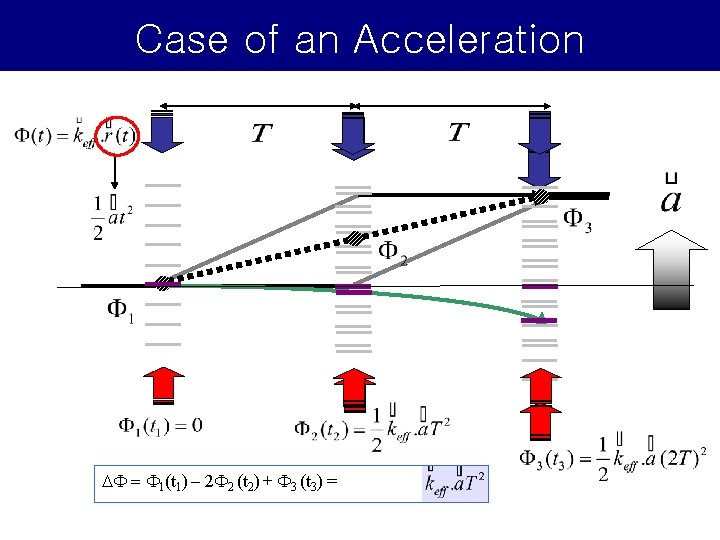
Case of an Acceleration DF = F 1(t 1) – 2 F 2 (t 2) + F 3 (t 3) =

Implementation of Raman Laser • Vertical Raman lasers Laser 1 • Retroreflect two (copropagating) Raman lasers Pulse 1 Reduces influence of path fluctuations (common mode) Þ 4 laser beams Þ 2 pairs of counterpropragating Raman lasers with opposite keff wavevectors Pulse 2 • Position of planes of equal phase difference attached to position of retroreflecting mirror Pulse 3 Laser 2 Miroir Interferometer measurement = relative displacement atoms/mirror

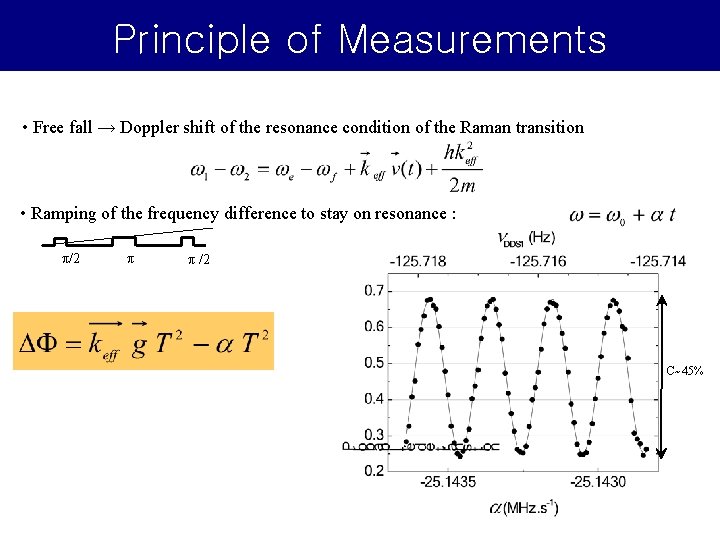
Principle of Measurements • Free fall → Doppler shift of the resonance condition of the Raman transition • Ramping of the frequency difference to stay on resonance : π/2 π π /2 C~45%

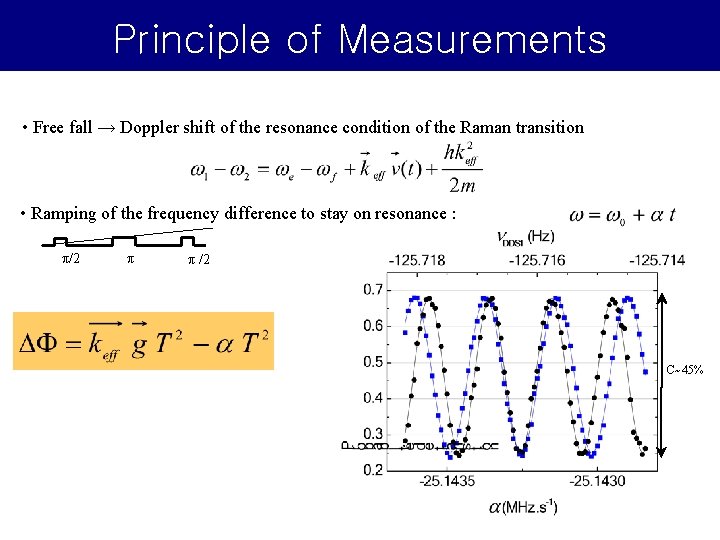
Principle of Measurements • Free fall → Doppler shift of the resonance condition of the Raman transition • Ramping of the frequency difference to stay on resonance : π/2 π π /2 C~45%

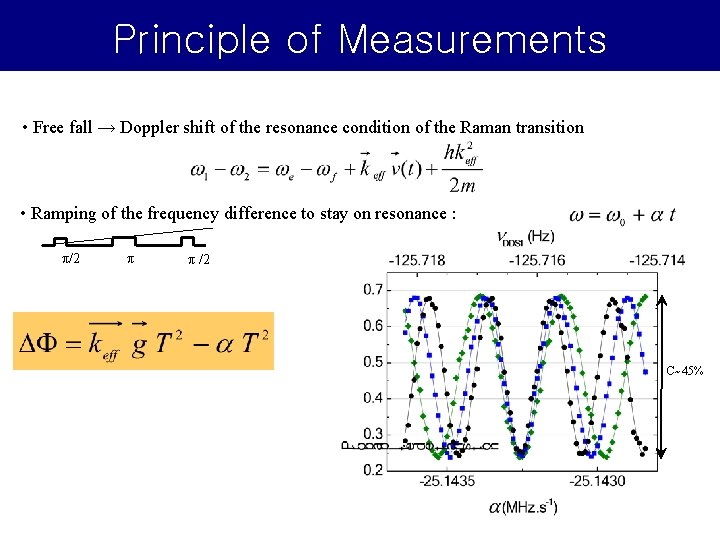
Principle of Measurements • Free fall → Doppler shift of the resonance condition of the Raman transition • Ramping of the frequency difference to stay on resonance : π/2 π π /2 C~45%

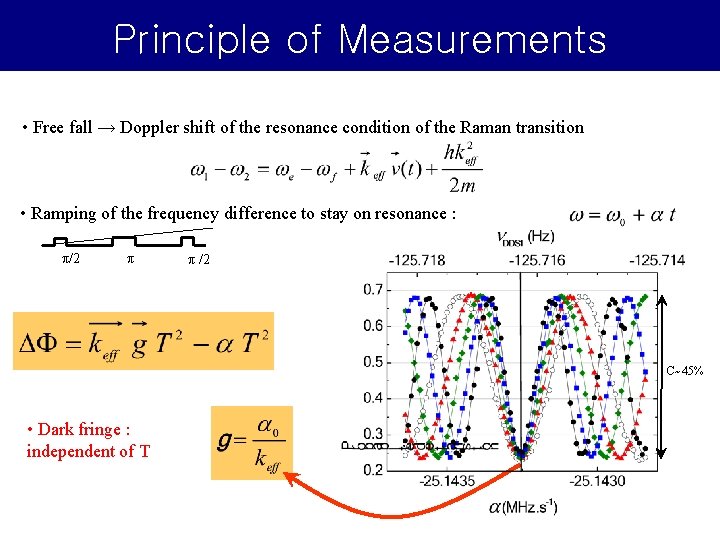
Principle of Measurements • Free fall → Doppler shift of the resonance condition of the Raman transition • Ramping of the frequency difference to stay on resonance : π/2 π π /2 C~45% • Dark fringe : independent of T

Experiments

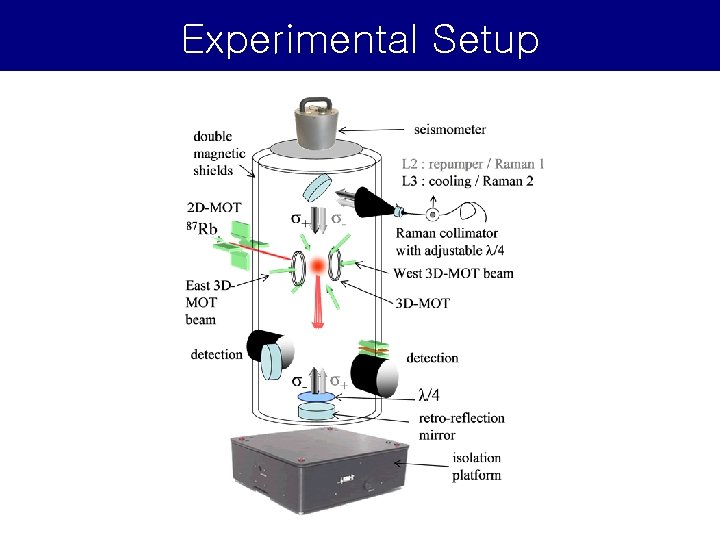
Experimental Setup 2 nd generation vacuum chamber • Titanium vacuum chamber (non magnetic) • 14 + 2 + 4 viewports • Indium seals • Pumps : 2 × getter pumps 50 l/s 1 × ion pump 2 l/s 4 × getter pills • Two layers magnetic shield • Retroreflecting mirror under vacuum

Experimental Setup

Experimental Setup Commercial fiber splitters Fibered angled MOT collimators Symmetric detection Passive isolation platform Baking 2~3 months at 120 °C

Optical Bench Compact : 60 by 90 cm 3 ECDL, 2 TA Key feature : Use the same lasers for Cooling and Raman beams

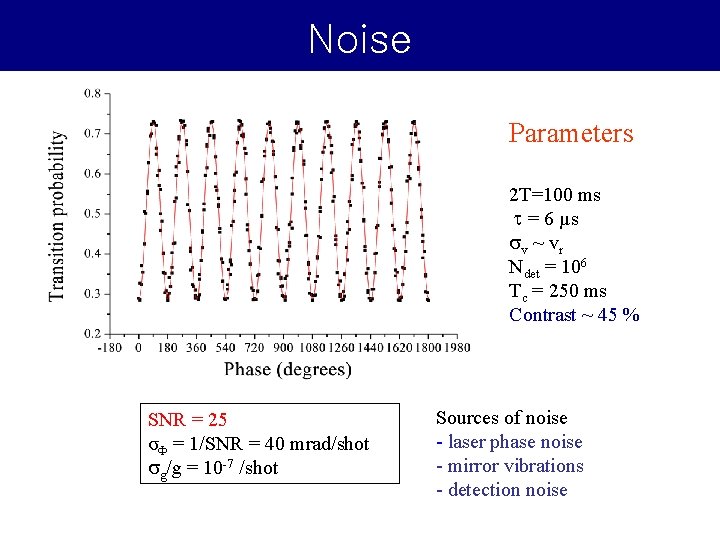
Noise Parameters 2 T=100 ms t = 6 µs s v ~ vr Ndet = 106 Tc = 250 ms Contrast ~ 45 % SNR = 25 σΦ = 1/SNR = 40 mrad/shot sg/g = 10 -7 /shot Sources of noise - laser phase noise - mirror vibrations - detection noise

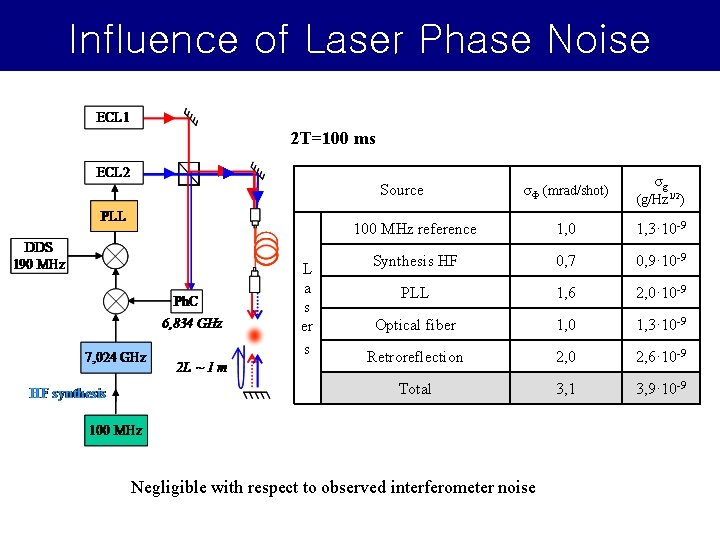
Influence of Laser Phase Noise 2 T=100 ms Source L a s er s σg σΦ (mrad/shot) (g/Hz 1/2) 100 MHz reference 1, 0 1, 3· 10 -9 Synthesis HF 0, 7 0, 9· 10 -9 PLL 1, 6 2, 0· 10 -9 Optical fiber 1, 0 1, 3· 10 -9 Retroreflection 2, 0 2, 6· 10 -9 Total 3, 1 3, 9· 10 -9 Negligible with respect to observed interferometer noise

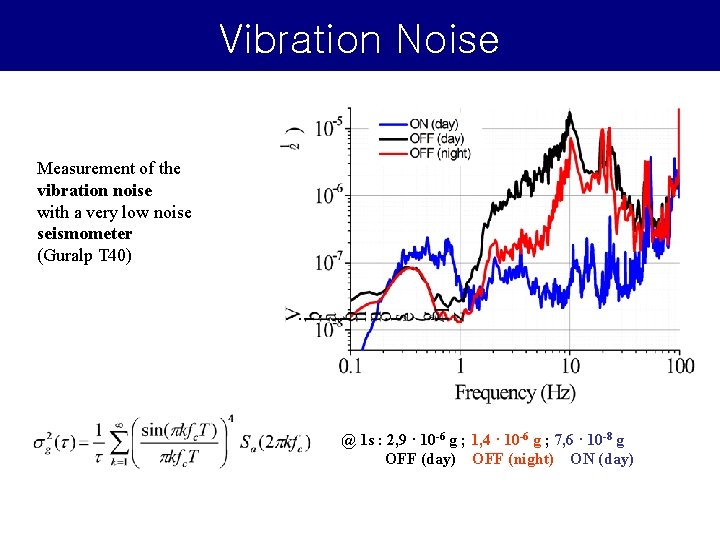
Vibration Noise Measurement of the vibration noise with a very low noise seismometer (Guralp T 40) @ 1 s : 2, 9 · 10 -6 g ; 1, 4 · 10 -6 g ; 7, 6 · 10 -8 g OFF (day) OFF (night) ON (day)

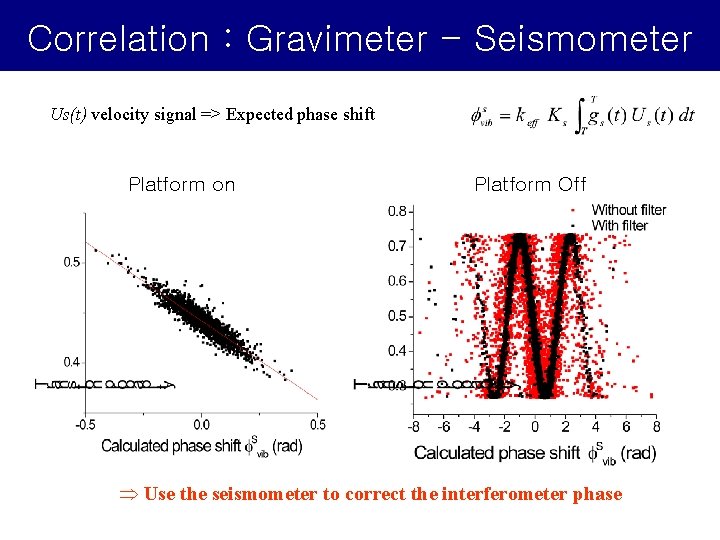
Correlation : Gravimeter - Seismometer Us(t) velocity signal => Expected phase shift Platform on Platform Off Þ Use the seismometer to correct the interferometer phase

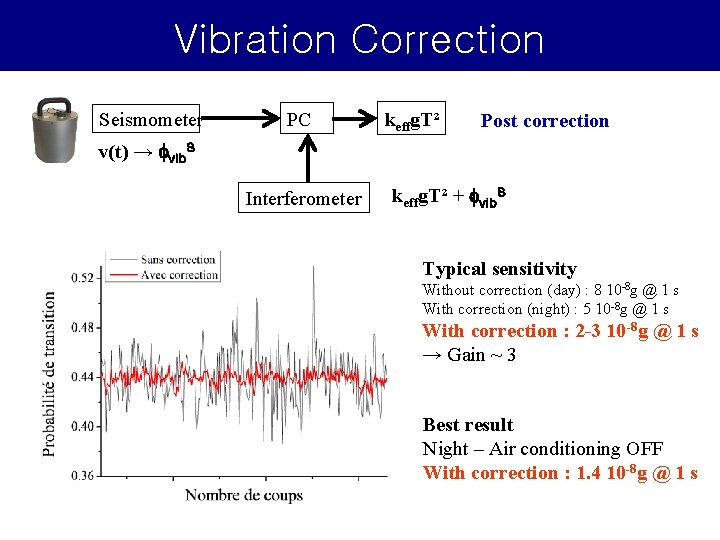
Vibration Correction Seismometer PC keffg. T² Post correction v(t) → fvib. S Interferometer keffg. T² + fvib. S Typical sensitivity Without correction (day) : 8 10 -8 g @ 1 s With correction (night) : 5 10 -8 g @ 1 s With correction : 2 -3 10 -8 g @ 1 s → Gain ~ 3 Best result Night – Air conditioning OFF With correction : 1. 4 10 -8 g @ 1 s

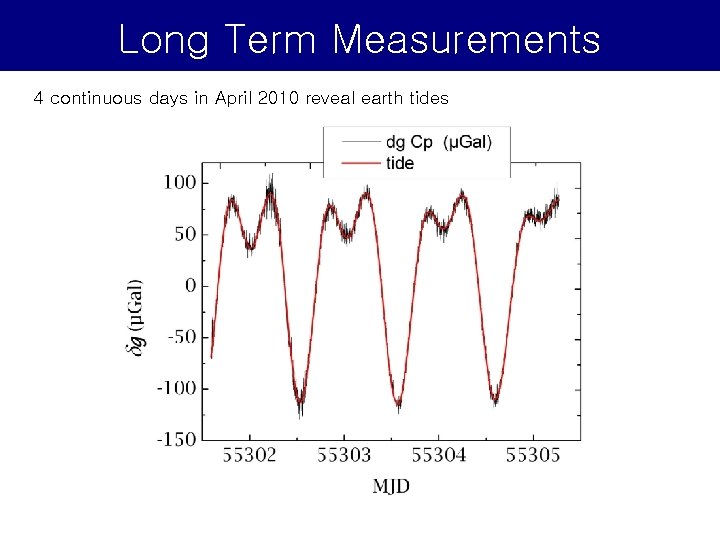
Long Term Measurements 4 continuous days in April 2010 reveal earth tides

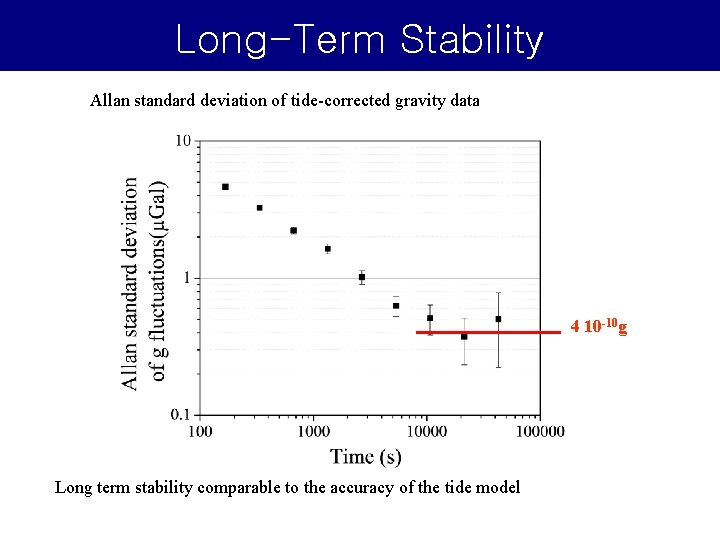
Long-Term Stability Allan standard deviation of tide-corrected gravity data 4 10 -10 g Long term stability comparable to the accuracy of the tide model

Wavefront Aberrations Wavefronts are not flat : gaussian beams, flatness of the optics … Case of a curvature → δφ = K. r 2 (with K = k 1/2 R) Δg < 10 -9 g with T = 2 µK R > 10 km ! → flatness better than λ/300 !!! Measure aberrations with wavefront sensor + excellent optics + colder atoms

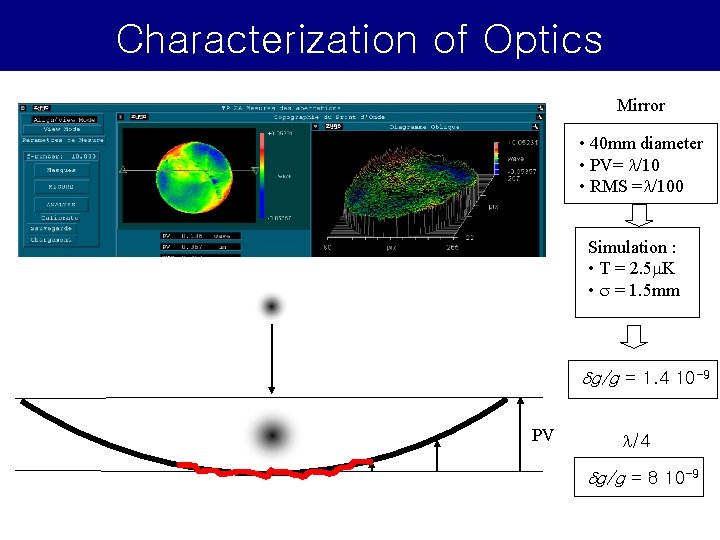
Characterization of Optics Mirror • 40 mm diameter • PV= l/10 • RMS =l/100 Simulation : • T = 2. 5 m. K • s = 1. 5 mm g/g = 1. 4 10 -9 PV l/4 g/g = 8 10 -9

Compact Atomic Gravimeter Principal demonstrations of key elements done ➡ New prototype under realization (automne 2010) ➡ High repetition rate (4 Hz) ➡ Expected performances: 50 µGal/√Hz Transportable device: field applications ➡ sensor head: -Few dm 3 -no mechanical moving part -Magnetic shield Pyramidal reflector (2 X 2 cm 2) 30 cm Laser and electronic ensemble: 19 inches/12 U

Conclusion CAG Laboratory experiment – (for Watt Balance project) Aimed at ultimate accuracy <10 -9 g Need for ultra cold atoms Towards on-field sensors Technology is now mature Þ Transfer to industry First step : Miniatom Soon on the market? l New schemes Trapped geometries : optical lattices, atom chips ? Further reduction in the size l New applications Geophysics, fundamental physics (tests of EP, space missions …)