Light oscillating electric and magnetic fields electromagnetic EM

Light: oscillating electric and magnetic fields electromagnetic (EM) radiation - travelling wave Characterize a wave by its wavelength, l, or frequency, n c=ln Black-body radiation Planck: vibrating atoms in a heated object give rise to the emitted EM radiation; these vibrations are quantized Energy of vibration = h n Photoelectric effect Einstein: light consists of massless particles called photons Ephoton = h c / l E of a mole of photons = No h n

Calculate the energy of each photon of blue light of frequency 6. 40 x 1014 Hz. What is the energy of a mole of photons of this frequency? E per photon = h n = (6. 626 x 10 -34 J s) (6. 40 x 1014 s-1) = 4. 20 x 10 -19 J E for a mole of photons = 4. 20 x 10 -19 J x 6. 023 x 1023/mole = 2. 53 x 105 J/mole or 253 k. J/mol

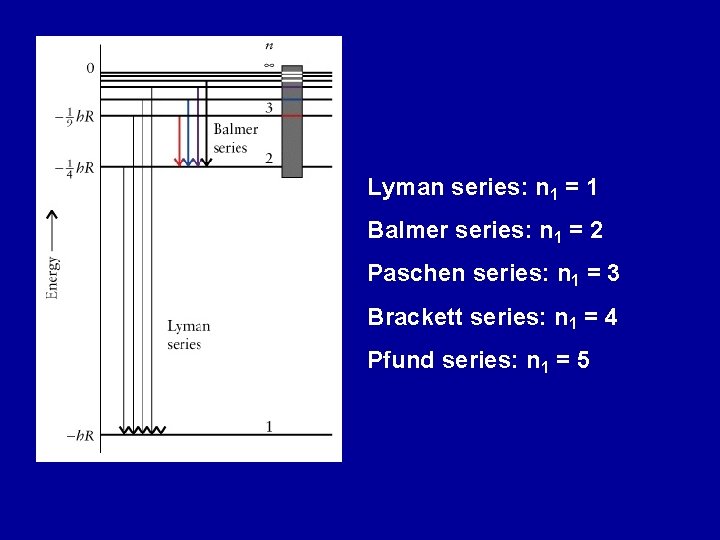
Atomic line spectra (nm) For the H atom n = ( 1 2 - 1 2 ) 3. 29 x 1015 s-1 n 2 n 1 = 3, 4, … n 2 = n 1 + 1, n 1 + 2, . . .

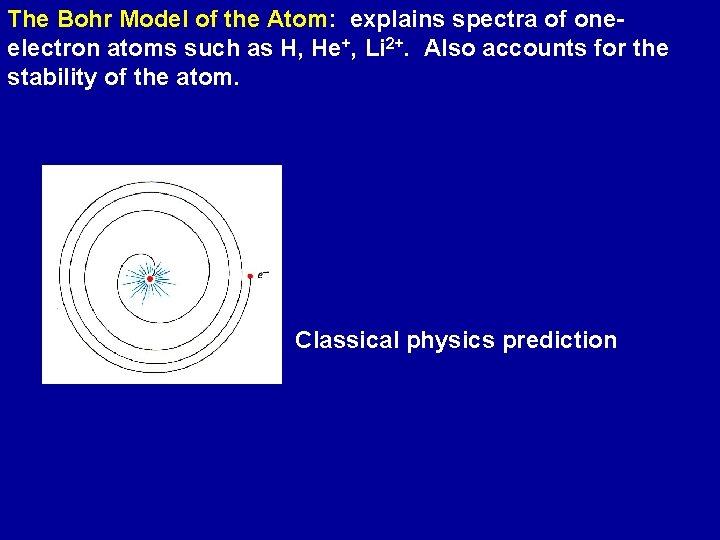
The Bohr Model of the Atom: explains spectra of oneelectron atoms such as H, He+, Li 2+. Also accounts for the stability of the atom. Classical physics prediction

Bohr theory 1) Quantization of angular momentum: For electrons, only those orbits, or energy state that have certain values of angular momentum are allowed Allowed orbits: angular momentum = n h / 2 p (n = 1, 2, 3, . . ) 2) As long as an electron stays in an allowed orbit it does not absorb or emit energy 3) Emission or absorption occurs only during transitions between allowed orbits. The emission and absorption are observed in spectra.

From the Bohr model angular momentum = Radius of allowed orbitals Z: positive charge on the nucleus ao : Bohr radius = 5. 29177 x 10 -11 m Total energy of electron in a stable orbital

Electrons can move from one allowed orbit to another, changing n is the energy absorbed or released equals the energy difference between allowed orbits of two different n values

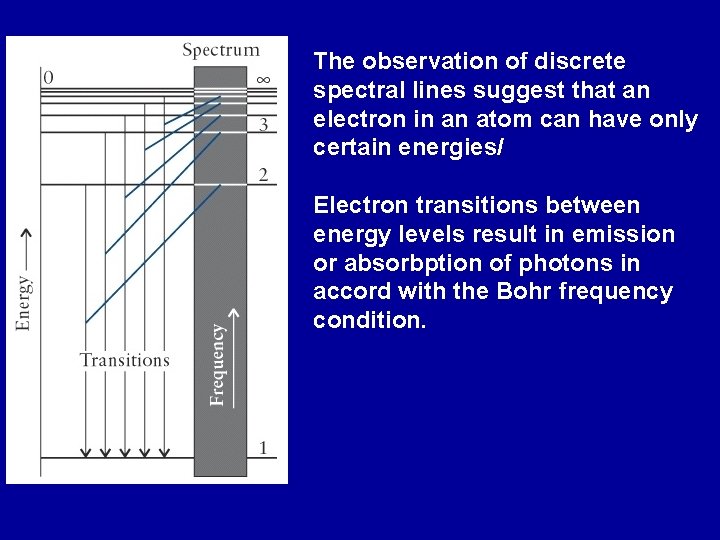
An electron in an atom can exist only in a series of discrete levels When an electron makes a transition, its energy changes from one of these levels to another. The difference in energy DE = Eupper - Elower is carried away as a photon The frequency of the photon emitted, n = DE/h

Energy from light of frequency n can also be absorbed by the H atoms if h n = DE = Eupper - Elower In this case, an electron in a lower energy level is excited to an upper energy level. If h n Eupper - Elower the electron cannot undergo a transition. The frequency of an individual spectral line is related to the energy difference between the two levels: h n = DE = Eupper - Elower animation

The observation of discrete spectral lines suggest that an electron in an atom can have only certain energies/ Electron transitions between energy levels result in emission or absorbption of photons in accord with the Bohr frequency condition.

Lyman series: n 1 = 1 Balmer series: n 1 = 2 Paschen series: n 1 = 3 Brackett series: n 1 = 4 Pfund series: n 1 = 5

Problems with Bohr’s theory Could not be used to determine energies of atoms with more than one electron. Unable to explain fine structure observed in H atom spectra Cannot be used to understand bonding in molecules, nor can it be used to calculate energies of even the simplest molecules. Bohr’s model based on classical mechanics, used a quantization restriction on a classical model.

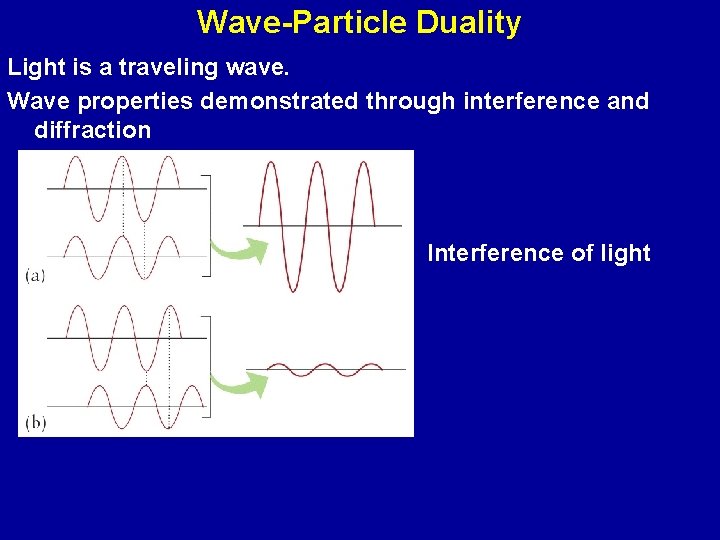
Wave-Particle Duality Light is a traveling wave. Wave properties demonstrated through interference and diffraction Interference of light

Diffraction of light Einstein’s experiments are explained by the “particle” nature of light - photons Light behaves as both a wave and a particle

Wave-Particle Duality of Matter Louis de Broglie: suggested that all particles should have wave like properties. Wavelength associated with a particle of mass m and speed v h l=mv h l= p where p = m v, the linear momentum of the particle

For a golf ball of mass 1. 62 ounces (0. 0459 kg), propelled at an average speed of 150. Mi/hr (67. 1 m/s), the de. Broglie wavelength is 2. 15 x 10 -34 m; too small to be measured Wavelength of an electron (me = 9. 11 x 10 -31 kg) moving at a speed of 3. 00 x 107 m/s is 2. 42 x 10 -11 m; corresponds to the X -ray region of the electromagnetic spectrum

Electron diffraction pattern (Davisson, Germer, Thompson, 1927)

The Uncertainty Principle In classical mechanics a particle has a definite path, or trajectory, on which location and linear momentum are specified at each instant. However, if a particle behaves as a wave, its precise location cannot be specified. Heisenberg’s uncertainty principle: impossible to fix both the position of an electron in an atom and its energy with any degree of certainty if the electron is described by a wave

Heisenberg uncertainty principle: if the location of a particle is known to within an uncertainty of Dx, then the linear momentum parallel to the x axis can be known only to within Dp, where Dx Dp ≥ 1 h 2 h h= 2 p Max Born: If the energy of an electron in an atom is known with a small uncertainty, then there must be a large uncertainty in its position. Can only assess the probability of finding an electron with a given energy within a given region of space

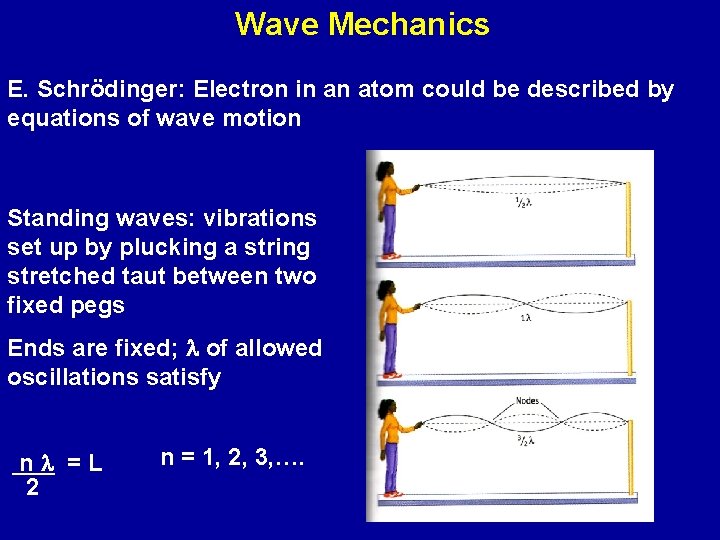
Wave Mechanics E. Schrödinger: Electron in an atom could be described by equations of wave motion Standing waves: vibrations set up by plucking a string stretched taut between two fixed pegs Ends are fixed; l of allowed oscillations satisfy nl =L 2 n = 1, 2, 3, ….

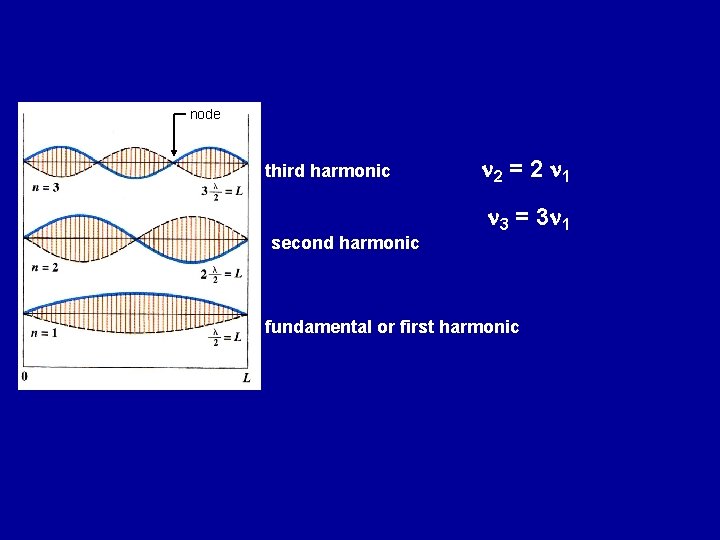
node third harmonic second harmonic n 2 = 2 n 1 n 3 = 3 n 1 fundamental or first harmonic

Standing waves - example of quantization; only certain discrete states allowed Electrons are wave-like and exist in stable standing waves, called stationary states, about the nucleus. Wave mechanics depicts the electron as a “wave-packet”

Stationary states with the circumference being divisible into an integral number of wavelengths From wave mechanics can show that allowed stationary states satisfy the condition: me v r = n h 2 p

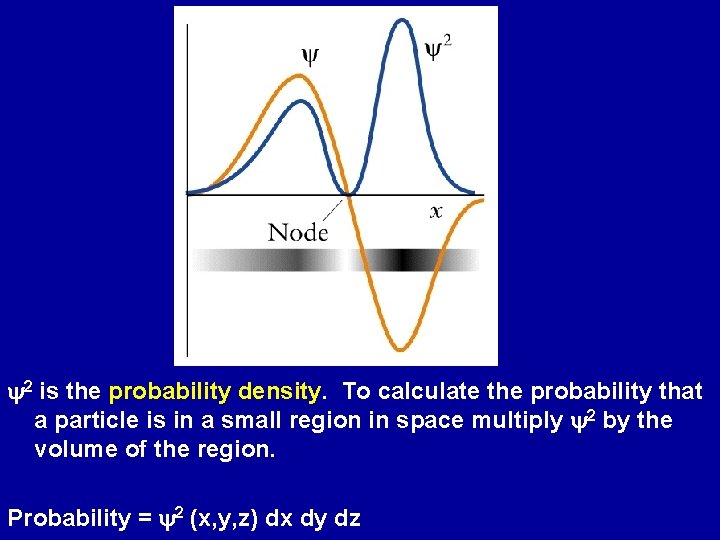
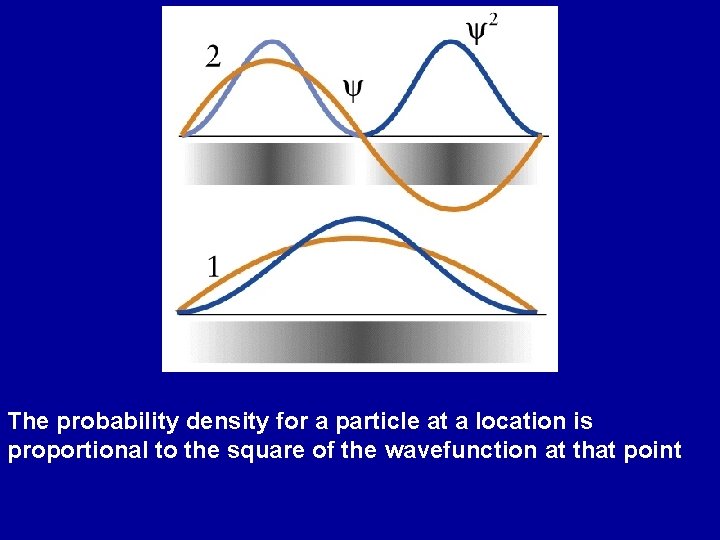
Wavefunctions and Energy Levels Since particles have wavelike properties cannot expect them to behave like point-like objects moving along precise trajectories. Erwin Schrödinger: Replace the precise trajectory of particles by a wavefunction (y), a mathematical function that varies with position Max Born: physical interpretation of wavefunctions. Probability of finding a particle in a region is proportional to y 2.

y 2 is the probability density. To calculate the probability that a particle is in a small region in space multiply y 2 by the volume of the region. Probability = y 2 (x, y, z) dx dy dz

Schrödinger Equation The Schrödinger equation describes the motion of a particle of mass m moving in a region where the potential energy is described by V(x). 2 y d -h 2 m dx 2 + V(x) y = E y (1 -dimension) Only certain wave functions are allowed for the electron in an atom The solutions to the equation defines the wavefunctions and energies of the allowed states

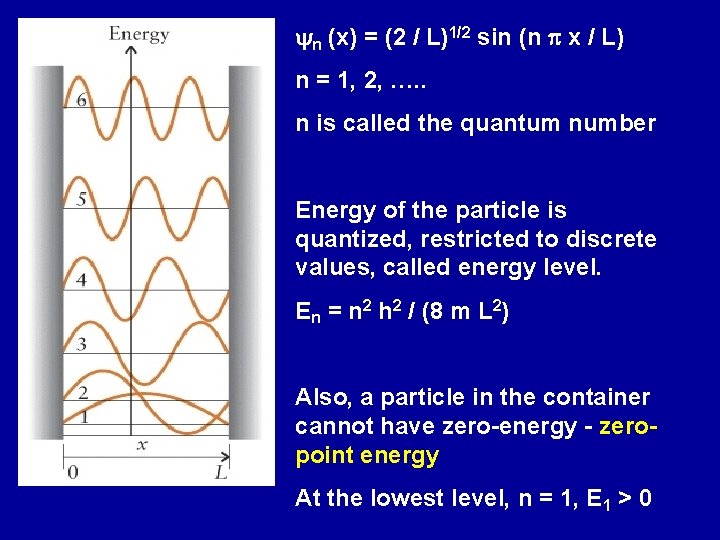
An outcome of Schrödinger’s equation is that the particle can only possess certain values of energy, i. e. energy of a particle is quantized. For example, one of the simplest example is that of a particle confined between two rigid walls a distance of L apart “particle in a box” Only certain wavelengths can exist in the box, just as a stretched guitar string can support only certain wavelengths.

yn (x) = (2 / L)1/2 sin (n p x / L) n = 1, 2, …. . n is called the quantum number Energy of the particle is quantized, restricted to discrete values, called energy level. En = n 2 h 2 / (8 m L 2) Also, a particle in the container cannot have zero-energy - zeropoint energy At the lowest level, n = 1, E 1 > 0

The probability density for a particle at a location is proportional to the square of the wavefunction at that point

To find the energy levels of an electron in the H atom, solve the Schrödinger equation. In the H atom the potential that the electron feels is the electrostatic interaction between it and the positive nucleus V(r ) = - e 2 / (4 p eo r) r: distance between the electron and the nucleus. Solution for allowed energy levels is: En = - h R n 2 n = 1, 2, . . . R = (me e 4) / (8 h 3 eo 2) = 3. 29 x 1015 Hz

Showed that quantum mechanics did indeed explain behavior of the electron Note that the energy of an electron bound in a H atom is always lower than that of a free electron (as indicated by the negative sign)

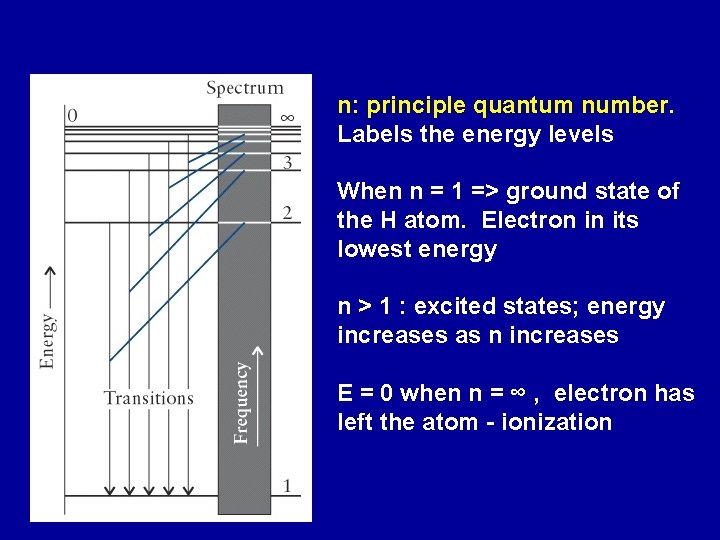
n: principle quantum number. Labels the energy levels When n = 1 => ground state of the H atom. Electron in its lowest energy n > 1 : excited states; energy increases as n increases E = 0 when n = ∞ , electron has left the atom - ionization