Light field microscopy Marc Levoy Ren Ng Andrew

Light field microscopy Marc Levoy, Ren Ng, Andrew Adams Matthew Footer, Mark Horowitz Stanford Computer Graphics Laboratory

Executive summary • captures the 4 D light field inside a microscope • yields perspective flyarounds and focal stacks from a single snapshot, but at lower spatial resolution • focal stack → deconvolution microscopy → volume data Ó 2006 Marc Levoy

Devices for recording light fields (using geometrical optics) big scenes small scenes • • • handheld camera gantry array of cameras plenoptic camera light field microscope [Buehler 2001] [Stanford 2002] [Wilburn 2005] [Ng 2005] (this paper) Ó 2006 Marc Levoy

Light fields at micron scales • wave optics must be considered – diffraction limits the spatial × angular resolution • most objects are no longer opaque – each pixel is a line integral through the object » of attenuation » or emission – can reconstruct 3 D structure from these integrals » tomography » 3 D deconvolution Ó 2006 Marc Levoy

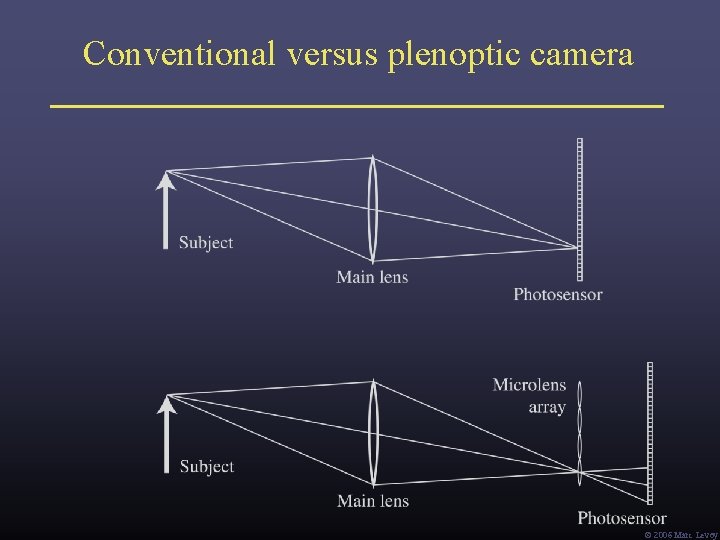
Conventional versus plenoptic camera Ó 2006 Marc Levoy

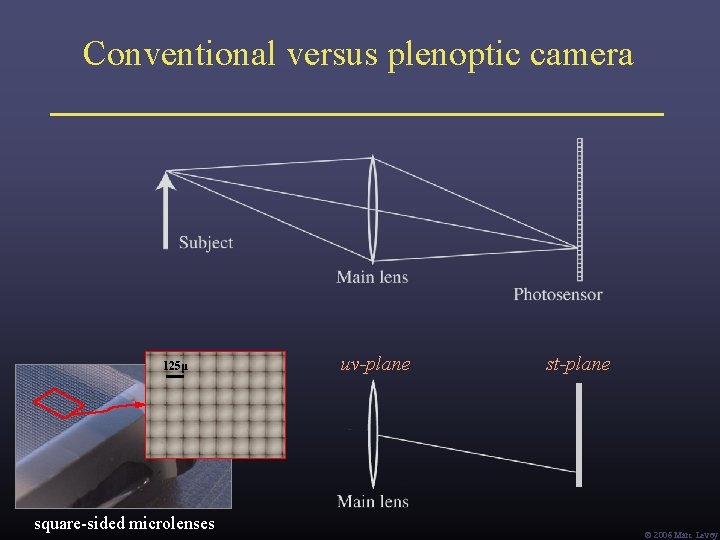
Conventional versus plenoptic camera 125μ square-sided microlenses uv-plane st-plane Ó 2006 Marc Levoy

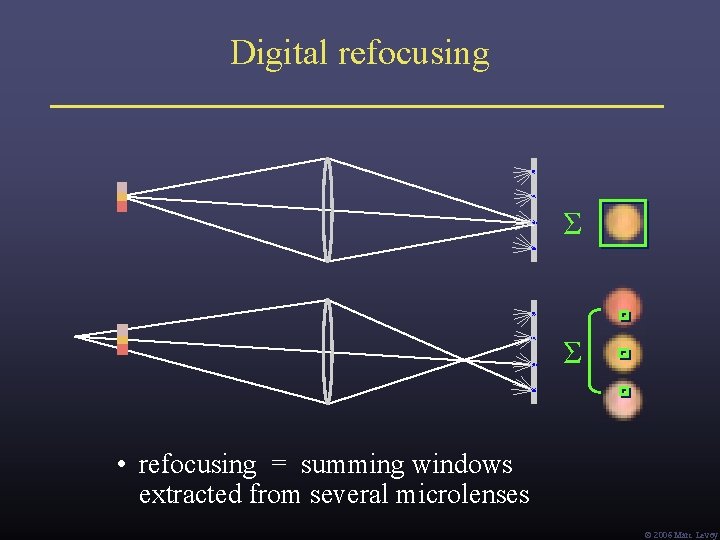
Digital refocusing Σ Σ • refocusing = summing windows extracted from several microlenses Ó 2006 Marc Levoy

Example of digital refocusing Ó 2006 Marc Levoy

Refocusing portraits Ó 2006 Marc Levoy

Macrophotography Ó 2005 Marc Levoy

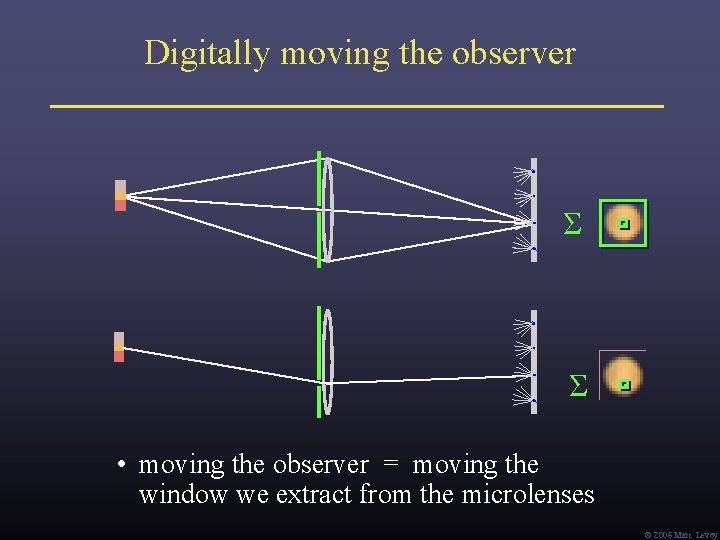
Digitally moving the observer Σ Σ • moving the observer = moving the window we extract from the microlenses Ó 2006 Marc Levoy

Example of moving the observer Ó 2006 Marc Levoy

Moving backward and forward Ó 2006 Marc Levoy

A light field microscope (LFM) eyepiece intermediate image plane objective specimen Ó 2006 Marc Levoy

A light field microscope (LFM) sensor eyepiece intermediate image plane objective specimen → reduced lateral resolution on specimen = 0. 26μ × 12 spots = 3. 1μ • 40 x / 0. 95 NA objective ↓ 0. 26μ spot on specimen × 40 x = 10. 4μ on sensor ↓ 2400 spots over 25 mm field • 1252 -micron microlenses ↓ 200 × 200 microlenses with 12 × 12 spots per microlens Ó 2006 Marc Levoy

A light field microscope (LFM) sensor 2. 5 mm 160 mm 0. 2 mm Ó 2006 Marc Levoy

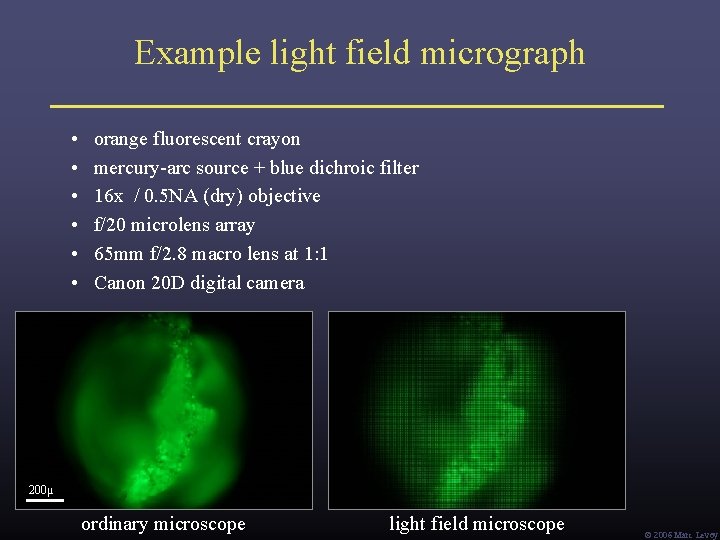
Example light field micrograph • • • orange fluorescent crayon mercury-arc source + blue dichroic filter 16 x / 0. 5 NA (dry) objective f/20 microlens array 65 mm f/2. 8 macro lens at 1: 1 Canon 20 D digital camera 200μ ordinary microscope light field microscope Ó 2006 Marc Levoy

The geometry of the light field in a microscope • microscopes make orthographic views • translating the stage in X or Y provides no parallax on the specimen f • out-of-plane features don’t shift position when they come into focus objective lenses are telecentric Ó 2006 Marc Levoy

Panning and focusing panning sequence focal stack Ó 2006 Marc Levoy

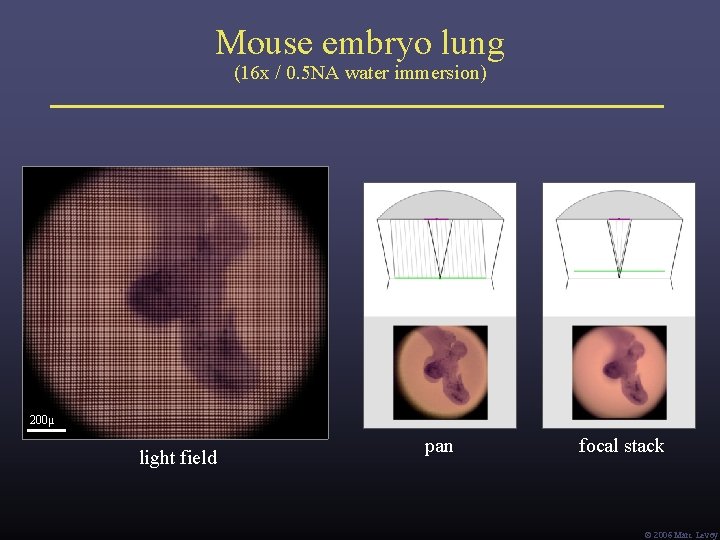
Mouse embryo lung (16 x / 0. 5 NA water immersion) 200μ light field pan focal stack Ó 2006 Marc Levoy

Axial resolution (a. k. a. depth of field) • wave term + geometrical optics term • ordinary microscope (16 x/0. 4 NA (dry), e = 0) (wave optics dominates) • with microlens array (e = 125μ) (geometrical optics dominates) • stopped down to one pixel per microlens → number of slices in focal stack = 12 Ó 2006 Marc Levoy

3 D reconstruction • confocal scanning [Minsky 1957] • shape-from-focus [Nayar 1990] • deconvolution microscopy [Agard 1984] – 4 D light field → digital refocusing → 3 D focal stack → deconvolution microscopy → 3 D volume data (UMIC SUNY/Stonybrook) (Noguchi) (Delta. Vision) Ó 2006 Marc Levoy

3 D deconvolution [Mc. Nally 1999] focus stack of a point in 3 -space is the 3 D PSF of that imaging system • • • object * PSF → focus stack {object} × {PSF} → {focus stack} {PSF} → {object} spectrum contains zeros, due to missing rays imaging noise is amplified by division by ~zeros reduce by regularization, e. g. smoothing {PSF} Ó 2006 Marc Levoy

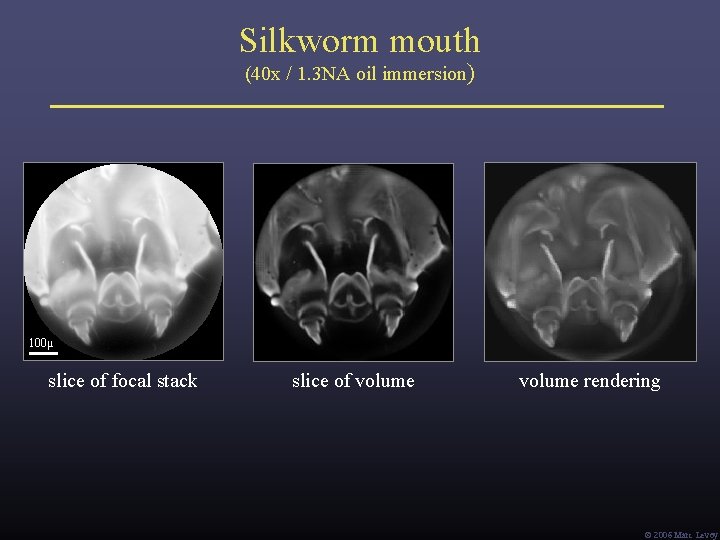
Silkworm mouth (40 x / 1. 3 NA oil immersion) 100μ slice of focal stack slice of volume rendering Ó 2006 Marc Levoy

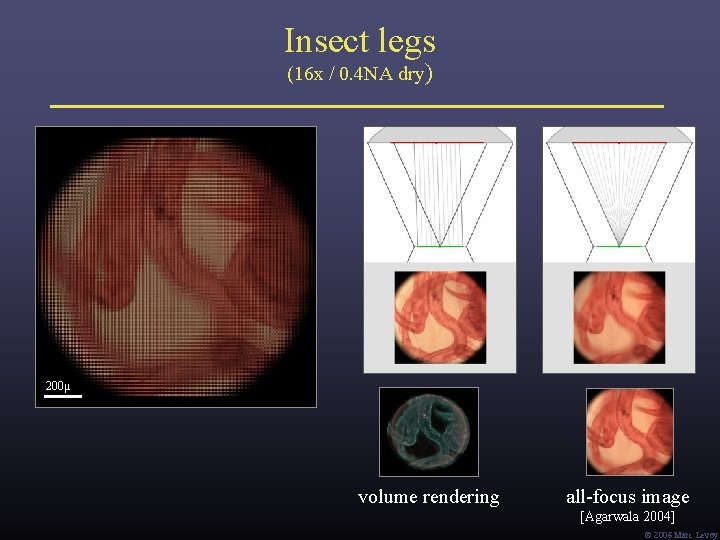
Insect legs (16 x / 0. 4 NA dry) 200μ volume rendering all-focus image [Agarwala 2004] Ó 2006 Marc Levoy

3 D reconstruction (revisited) • 4 D light field → digital refocusing → 3 D focal stack → deconvolution microscopy → 3 D volume data (Delta. Vision) • 4 D light field → tomographic reconstruction → 3 D volume data (from Kak & Slaney) Ó 2006 Marc Levoy

Implications of this equivalence • light fields of minimally scattering volumes contain only 3 D worth of information, not 4 D • the extra dimension serves to reduce noise, but could be re-purposed? Optical Projection Tomography [Sharpe 2002] Ó 2006 Marc Levoy

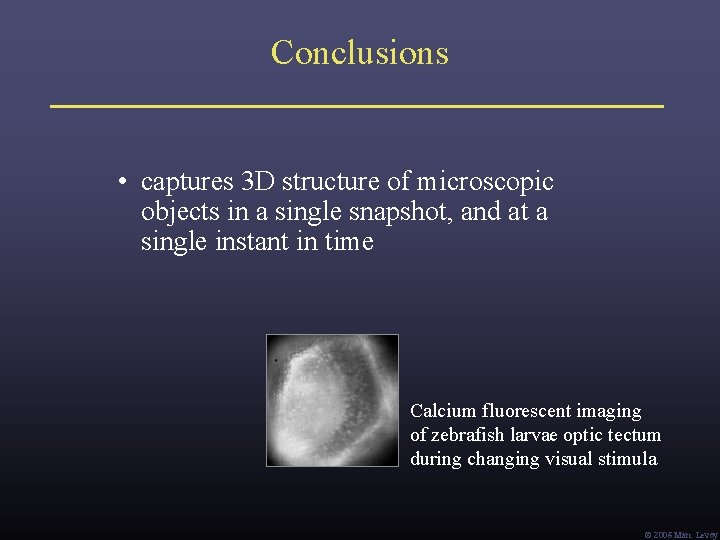
Conclusions • captures 3 D structure of microscopic objects in a single snapshot, and at a single instant in time Calcium fluorescent imaging of zebrafish larvae optic tectum during changing visual stimula Ó 2006 Marc Levoy

Conclusions • captures 3 D structure of microscopic objects in a single snapshot, and at a single instant in time but. . . • sacrifices spatial resolution to obtain control over viewpoint and focus • 3 D reconstruction fails if specimen is too thick or too opaque Ó 2006 Marc Levoy

Future work • extending the field of view by correcting digitally for objective aberrations Nikon 40 x 0. 95 NA (dry) Plan-Apo Ó 2006 Marc Levoy

Future work • extending the field of view by correcting digitally for objective aberrations • microlenses in the illumination path → an imaging microscope scatterometer 200μ angular dependence of reflection from single squid iridophore Ó 2006 Marc Levoy

http: //graphics. stanford. edu/projects/lfmicroscope Ó 2006 Marc Levoy