Lidhja e bobinave Lidhja serike e bobinave Bobinatsikurse
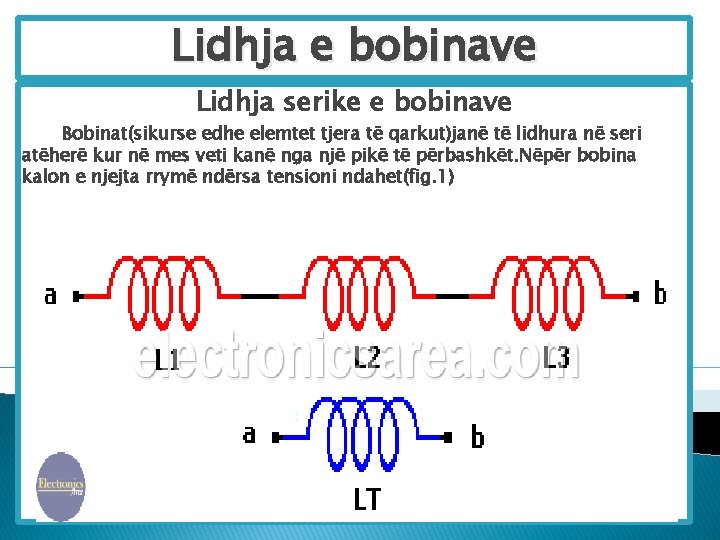
Lidhja e bobinave Lidhja serike e bobinave Bobinat(sikurse edhe elemtet tjera të qarkut)janë të lidhura në seri atëherë kur në mes veti kanë nga një pikë të përbashkët. Nëpër bobina kalon e njejta rrymë ndërsa tensioni ndahet(fig. 1)

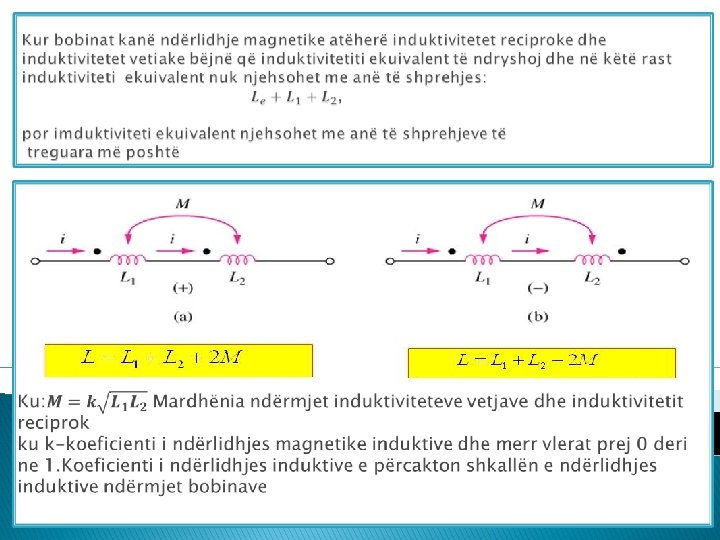
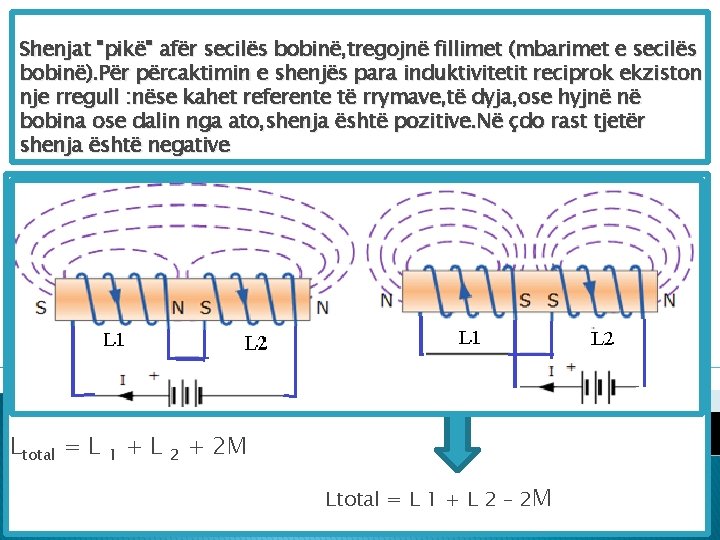
Shenjat "pikë" afër secilës bobinë, tregojnë fillimet (mbarimet e secilës bobinë). Për përcaktimin e shenjës para induktivitetit reciprok ekziston nje rregull : nëse kahet referente të rrymave, të dyja, ose hyjnë në bobina ose dalin nga ato, shenja është pozitive. Në çdo rast tjetër shenja është negative Ltotal = L 1 + L 2 + 2 M Ltotal = L 1 + L 2 – 2 M
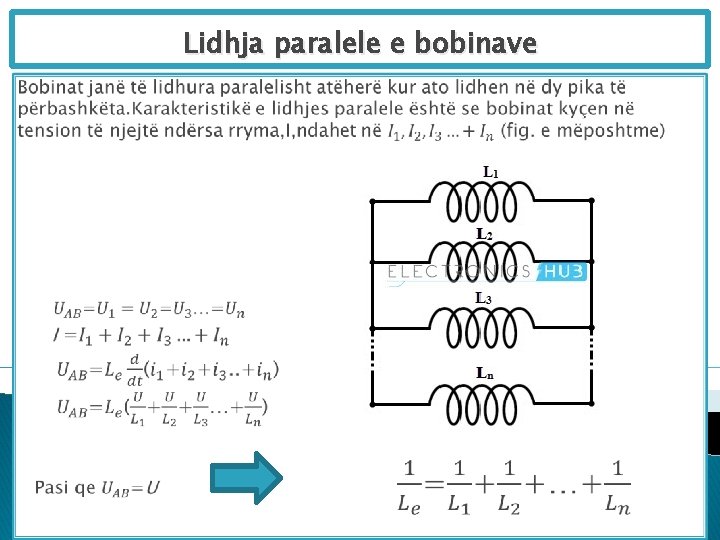
Lidhja paralele e bobinave
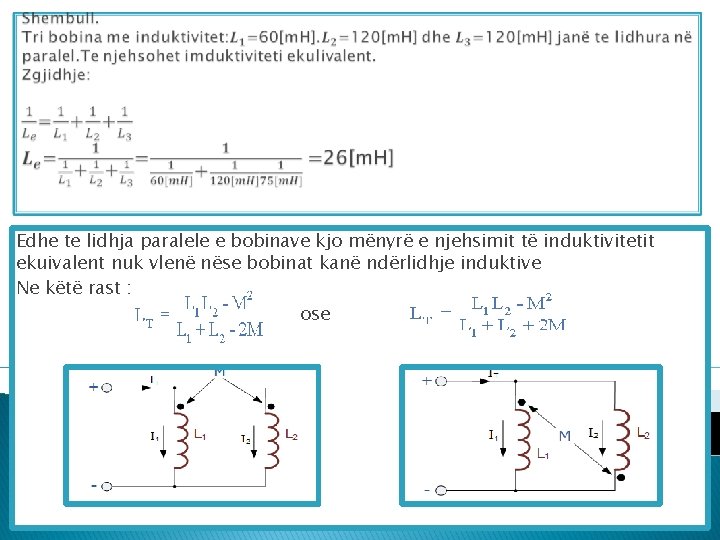
Edhe te lidhja paralele e bobinave kjo mënyrë e njehsimit të induktivitetit ekuivalent nuk vlenë nëse bobinat kanë ndërlidhje induktive Ne këtë rast : ose
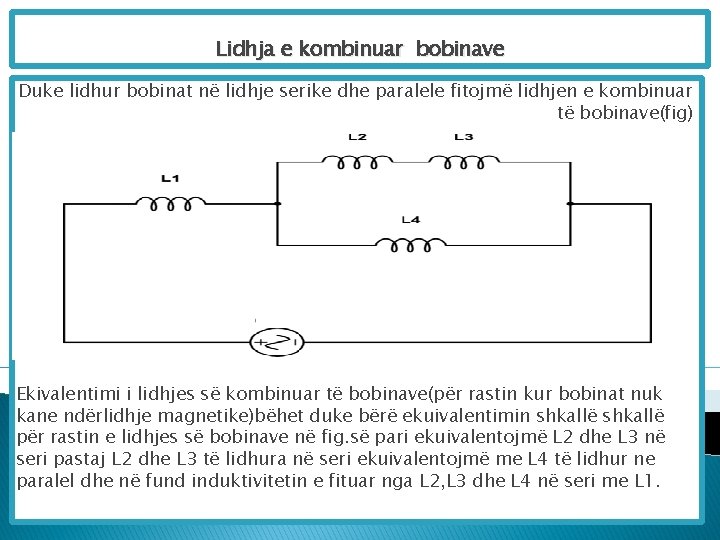
Lidhja e kombinuar bobinave Duke lidhur bobinat në lidhje serike dhe paralele fitojmë lidhjen e kombinuar të bobinave(fig) Ekivalentimi i lidhjes së kombinuar të bobinave(për rastin kur bobinat nuk kane ndërlidhje magnetike)bëhet duke bërë ekuivalentimin shkallë për rastin e lidhjes së bobinave në fig. së pari ekuivalentojmë L 2 dhe L 3 në seri pastaj L 2 dhe L 3 të lidhura në seri ekuivalentojmë me L 4 të lidhur ne paralel dhe në fund induktivitetin e fituar nga L 2, L 3 dhe L 4 në seri me L 1.
![Shembull. Të njehsohet induktiviteti e kuivalent nëse bobinat L 1=100[m. H], L 2=200[m. H], Shembull. Të njehsohet induktiviteti e kuivalent nëse bobinat L 1=100[m. H], L 2=200[m. H],](http://slidetodoc.com/presentation_image_h/b39fc0c8687bdfedc5d8b6f78ef85183/image-8.jpg)
Shembull. Të njehsohet induktiviteti e kuivalent nëse bobinat L 1=100[m. H], L 2=200[m. H], L 3=300[m. H] dhe L 4=400[m. H] janë të lidhura si në figurën e mëposhtme. �
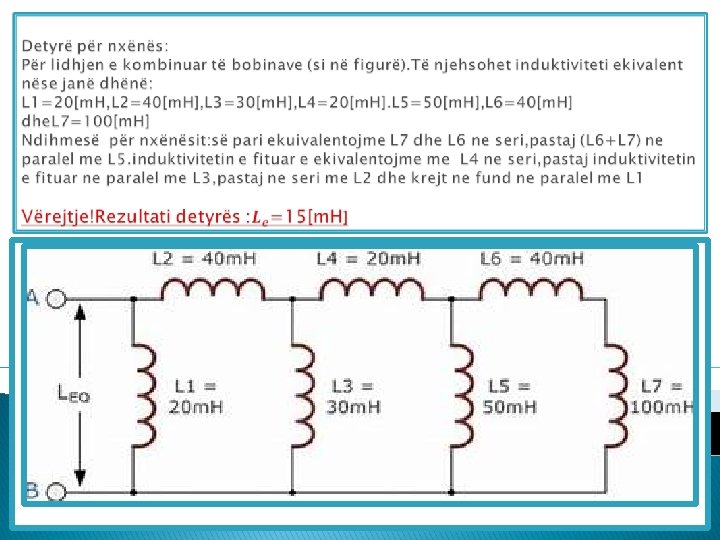
- Slides: 9