Liczby rzeczywiste M Wszystkie liczby ktre odpowiadaj punktom

Liczby rzeczywiste ©M

Wszystkie liczby, które odpowiadają punktom na osi liczbowej, nazywamy liczbami rzeczywistymi. Podzbiory liczb rzeczywistych Zbiór liczb naturalnych Zbiór liczb całkowitych Zbiór liczb wymiernych ©M Zbiór liczb niewymiernych

Liczby naturalne N = { 0, 1, 2, 3, ……, n-1, n, n+1, . . } v Jeżeli różne od zera liczby naturalne n, m i k spełniają równość n = m·k, to liczba n jest podzielna przez m i przez k. Liczby m i k to dzielniki liczby n, a liczba n to wielokrotność liczby m i k. v Liczba pierwsza to liczba naturalna k, która ma dwa różne dzielniki: samą siebie oraz 1. ©M

v Liczba złożona to liczba naturalna mająca więce niż dwa dzielniki. v Liczby względnie pierwsze to dwie liczby naturalne których jedynym dzielnikiem jest liczba 1. v Rozkład na czynniki pierwsze to przedstawienie liczby naturalnej w postaci iloczynu liczb pierwszych. przykład 420 2 210 2 105 3 35 5 7 7 1 420 = 22 · 3· 5· 7 ©M

Zasadnicze twierdzenie arytmetyki Każda liczba złożona jest iloczynem liczb pierwszych. Rozkład ten jest dla danej liczby jednoznaczny z dokładnością do porządku czynników. NWD(m, n) – największy wspólny dzielnik liczb naturalnych m, n to największy ze wszystkich dzielników tych liczb. NWW(m, n) - najmniejsza wspólna wielokrotność liczb naturalnych m, n jest to najmniejsza ze wszystkich wspólnych wielokrotności tych liczb. ©M

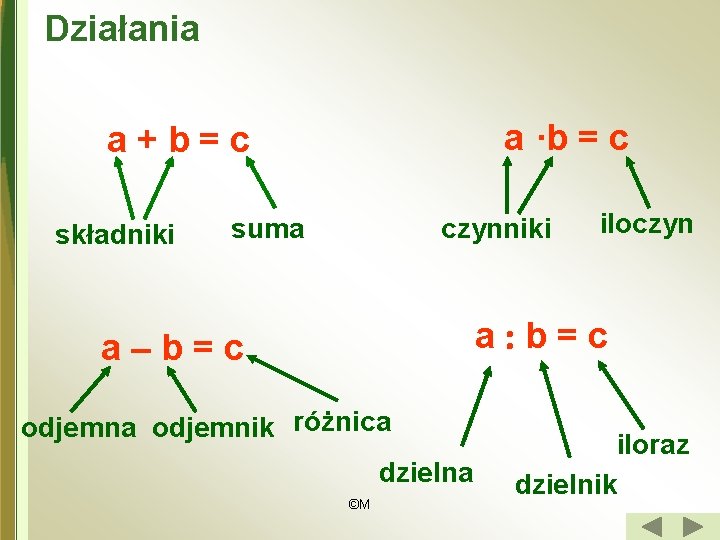
Działania a ·b = c a+b=c składniki suma czynniki iloczyn a b=c a–b=c odjemna odjemnik różnica dzielna ©M iloraz dzielnik

Cechy podzielności dzielnik cechy podzielności 2 3 4 cyfrą jedności jest 0, 2, 4, 6 albo 8 5 6 8 ostatnią cyfrą liczby jest 5 albo 0 9 suma cyfr liczby ©M dzieli się przez 9 suma cyfr liczby jest podzielna przez 3 liczba utworzona przez dwie ostatnie cyfry dzieli się przez 4 liczba jest podzielna przez 2 i przez 3 liczba utworzona przez trzy ostatnie cyfry tej liczby dzieli się przez 8

Liczby całkowite to liczby naturalne i do nich przeciwne. C = {…. . . -3, -2, -1, 0, 1, 2, 3, …. . . } Liczby parzyste - to liczby, które są podzielne przez 2; postać tej liczby a=2 k, gdzie k C. Liczby nieparzyste - to liczby, które nie są podzielne przez 2; postać a = 2 k +1 gdzie k C ©M

Liczby wymierne , gdzie m, n C i n 0 to liczby postaci Liczbę wymierną możemy zapisać w postaci ułamka dziesiętnego. Rozwinięcie dziesiętne liczby otrzymujemy, wykonując dzielenie p przez q. Np. okres rozwinięcia dziesiętnego ©M Długość okresu 1 – liczba cyfr, z których składa się okres.

v Jeżeli liczba rzeczywista ma rozwinięcie dziesiętne skończone lub nieskończone okresowe, to liczba jest wymierna. v Każdą liczbę wymierną można przedstawić w postaci rozwinięcia dziesiętnego skończonego i nieskończonego okresowego. Zamienić na ułamek liczbę 0, (23) Oznaczamy przez a=0, 2323……. · 100 a = 23, 232323……. czyli 100 a = 23 +a a więc po odjęciu mamy 99 a = 23 Stąd ©M

Reguły działań na liczbach wymiernych ©M

Liczby niewymierne to liczby, które nie możemy przedstawić w postaci ułamka. Przykłady: v. Każda liczba niewymierna ma rozwinięcie dziesiętne nieskończone i nieokresowe. ©M

Konstrukcja odcinków o długościach niewymiernych ©M

Każda liczba rzeczywista jest liczbą wymierną albo niewymierną. R Zależności v N C W R v. N C =C v W IW = R v. W C=C v. N C W=W v. N C=N v W IW = v. W N=N ©M