Licenciatura Plena em Cincias Naturais e MatemticaUFMT Mdulo

Licenciatura Plena em Ciências Naturais e Matemática-UFMT Módulo VIII Habilitação: Matemática SEQÜÊNCIAS E SÉRIES Professores: Demilson, Geraldo, Gladys, Luzia, Vinicius e William CUIABÁ/JANEIRO/2007

SEQÜÊNCIAS Na linguagem do dia-a-dia, o termo seqüência significa uma sucessão de coisas em uma ordem determinada (cronológica, de tamanho, ou lógica). Ex. dias da semana, meses do ano, figuras semelhantes. Em Matemática, seqüência é usada para denotar uma sucessão de números cuja ordem é determinada por uma lei ou função (cujo domínio é o conjunto dos números naturais). Ex. conjunto dos nos pares, dos múltiplos de 7. (ANTON, 2000, p. 38 e 40)

SEQÜÊNCIAS As seqüências numéricas podem ser: Finita a) A seqüência dos quatro primeiros números naturais múltiplos de 5: (0, 5, 10, 15) (a 1, a 2, a 3, a 4) b) A seqüência dos números de dias dos 12 meses de um ano bissexto: (31, 29, 31, 30, 31) (a 1, a 2, a 3, a 4, a 5, a 6, a 7, a 8, a 9, a 10, a 11, a 12)

SEQÜÊNCIAS Infinita a) A seqüência dos números naturais ímpares: (1, 3, 5, 7, 9, 11, . . . ) (a 1, a 2, a 3, a 4, a 5, a 6, . . . , an, . . . ) b) A seqüência dos números quadrados perfeitos: (1, 4, 9, 16, 25, 36, . . . )

SEQÜÊNCIAS Seqüência ou Progressão Aritmética (PA) a) (2, 7, 12, 17, . . . ) 7 – 2 = 5; 12 – 7 = 5; 17 – 12 = 5; . . . Crescente ou a 2 = 7 = 2 + 5; a 3 = 12 = 7 + 5; a 4 = 17 = 12 + 5; . . . Decrescente b) (20, 10, 0, – 10, – 20, . . . ) 10 – 20 = – 10; 0 – 10 = – 10; . . . ou a 2 = 10 = 20 + (– 10); a 4 = – 10 = 0 + (– 10); . . . a 3 = 0 = 10 + (– 10);

SEQÜÊNCIAS PA é toda seqüência de números na qual: I. a partir do segundo termo, a diferença entre cada termo e o seu precedente (anterior) é CONSTANTE; ou II. Cada um de seus termos, exceto o primeiro, é igual ao precedente, somado a um número CONSTANTE. Essa constante chama-se RAZÃO (r).

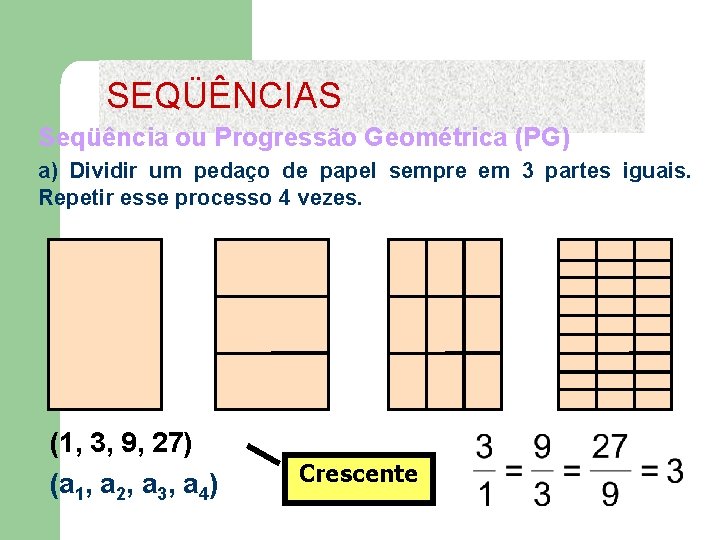
SEQÜÊNCIAS Seqüência ou Progressão Geométrica (PG) a) Dividir um pedaço de papel sempre em 3 partes iguais. Repetir esse processo 4 vezes. (1, 3, 9, 27) (a 1, a 2, a 3, a 4) Crescente

SEQÜÊNCIAS Na seqüência (1, 3, 9, 27) podemos ainda notar que: a 2 = 3 = 1. 3; a 3 = 9 = 3. 3; a 4 = 27 = 9. 3 b) (512, 128, 32, 8, 2, . . . ) Decrescente

SEQÜÊNCIAS PG é toda seqüência de números não-nulos na qual: I. a partir do segundo termo, o quociente da divisão de cada termo pelo seu precedente é CONSTANTE; ou II. Cada um de seus termos, exceto o primeiro, é igual ao precedente, multiplicado por uma CONSTANTE. Esse quociente ou fator é chamado de RAZÃO (q) da progressão geométrica.

SEQÜÊNCIAS Seqüência formada por uma lei ou função ( )

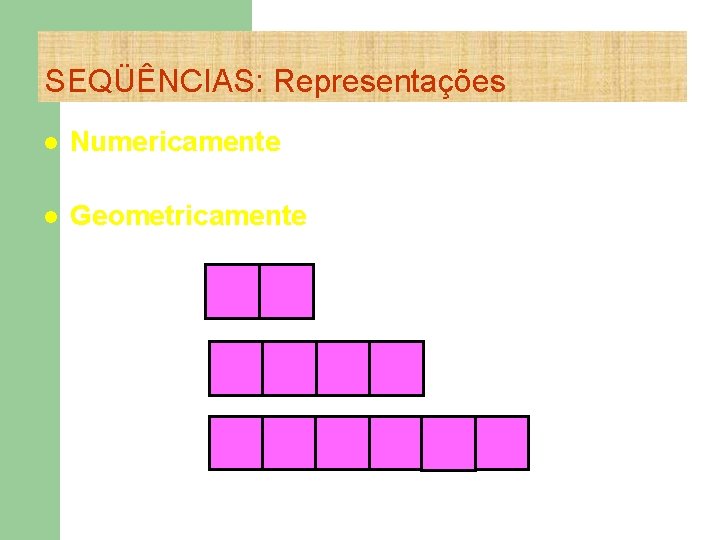
SEQÜÊNCIAS: Representações l Numericamente: (2, 4, 6, . . . ) l Geometricamente

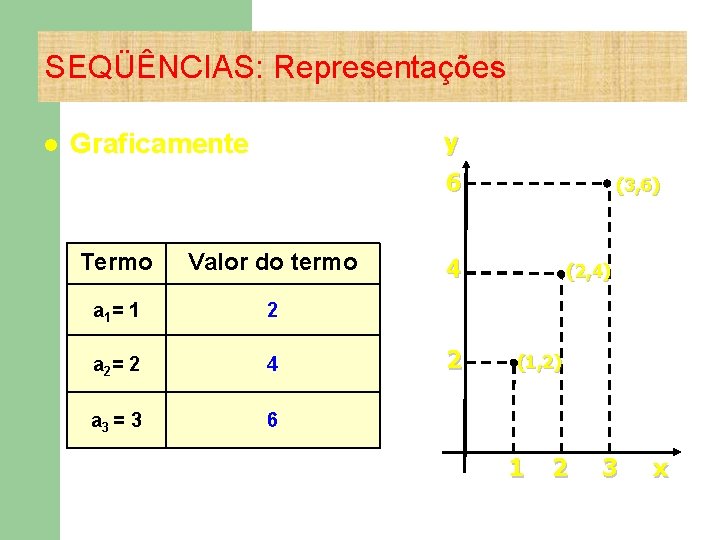
SEQÜÊNCIAS: Representações l y Graficamente 6 Termo Valor do termo a 1 = 1 2 a 2 = 2 4 a 3 = 3 6 (3, 6) 4 2 (2, 4) (1, 2) 1 2 3 x

SEQÜÊNCIAS: Representações Algebricamente f(n) = an = 2 n, para n lΝ/n 1 l l Por Chaves + 2 n n=1

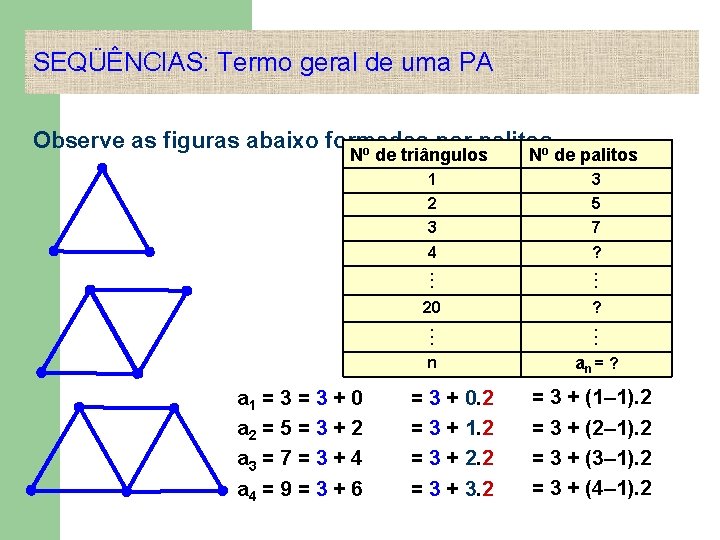
SEQÜÊNCIAS: Termo geral de uma PA Observe as figuras abaixo formadas por palitos. o o N de triângulos a 1 = 3 + 0 a 2 = 5 = 3 + 2 a 3 = 7 = 3 + 4 a 4 = 9 = 3 + 6 N de palitos 1 2 3 3 5 7 4. . . ? . . . 20. . . n ? . . . = 3 + 0. 2 = 3 + 1. 2 = 3 + 2. 2 = 3 + 3. 2 an = ? = 3 + (1– 1). 2 = 3 + (2– 1). 2 = 3 + (3– 1). 2 = 3 + (4– 1). 2

SEQÜÊNCIAS: Termo geral de uma PA a 20 = 3 + (20 – 1). 2 = 3 + 38 = 41. . . an = 3 + (n – 1). 2 termo geral dessa PA O termo geral também pode ser expresso como função f(n) = an = 3 + (n – 1). 2 f(n) = 2 n + 1 Generalizando – o termo geral de uma PA: an = a 1 + (n – 1). r

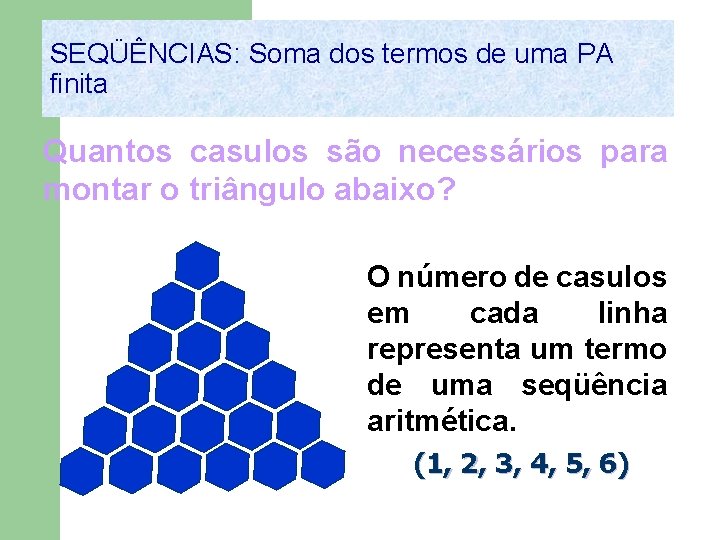
SEQÜÊNCIAS: Soma dos termos de uma PA finita Quantos casulos são necessários para montar o triângulo abaixo? O número de casulos em cada linha representa um termo de uma seqüência aritmética. (1, 2, 3, 4, 5, 6)

SEQÜÊNCIAS: Soma dos termos de uma PA finita S 6=[(1 + 6). 6]/2 = 21 Sn = [(a 1 + an). n]/2

SEQÜÊNCIAS: Termo geral de uma PG Voltando à divisão da folha de papel, fazendo agora inúmeras vezes essa divisão. Estágios da divisão Original E 0 : 0 E 1 : 1 E 2 : 2 E 3 : 3. . . E 12: 12. . . En : an = 1. 3 n-1 a 1 = 1 a 2 = 3 a 3 = 9 a 4 = 27 n = 1. 30. 3 = 1. 31. 3 = 1. 32. 3 = 1. 33 No de regiões a 1 = 1 a 2 = 3 a 3 = 9 a 4 = 27. . . ? . . . an = ? = 1. 31 -1 = 1. 32 -1 = 1. 33 -1 = 1. 34 -1

SEQÜÊNCIAS: Termo geral de uma PG an = 1. 3 n-1 Termo geral da PG para esse exemplo dado Generalizando: Como nesse exemplo tínhamos a 1 = 1 e q = 3, então an = a 1. qn-1 Onde: an = termo geral; a 1 = 1 o termo da seqüência; n = no de termos da PG (até an); q = razão.

SEQÜÊNCIAS: Soma dos n termos de uma PG finita Somando os termos da seqüência (1, 3, 9, 27) S = 1 + 3 + 9 + 27 ou 3 = 1. 3 9 = 3. 3 27 = 9. 3 81 = 27. 3 Assim, 3. S = 3 + 9 + 27 + 81 – S = 1 + 3 + 9 + 27 3. S – S = 81 – 1 S = 80 : 2 = 40

SEQÜÊNCIAS: Soma dos n termos de uma PG finita Generalizando: consideremos uma PG finita (a 1, a 2, a 3, a 4, a 5, a 6, . . . , an) de razão q 1. Sn = a 1 + a 2 + a 3 +. . . + an-1 + an (I) Multiplicamos ambos os membros por q: Sn. q = a 1 q + a 2 q + a 3 q +. . . + an-1 q + anq Sn. q = a 2 + a 3 +. . . + an-1 + an+1 (II) Como an+1 = a 1 qn, fazemos (II) – (I): Sn. q – Sn = a 1 qn – a 1 (q – 1)Sn = a 1(qn – 1) Sn = [a 1(qn – 1)] : (q – 1), q 1