lgebra Clculo Vectorial Matemticas para Computacin Dr Felipe

Álgebra. Cálculo Vectorial Matemáticas para Computación Dr. Felipe Orihuela-Espina

Contenidos § Vectores y espacios vectoriales No forma parte del § Espacios/campos vectoriales temario así que la veremos MUY rápido. § Topología y Manifolds § Morfismos: homeomorfismos / difeomorfismos / etc-morfismos © 2013 -6. Dr. Felipe Orihuela-Espina 2

Lecturas recomendadas § Cálculo vectorial y topología § Anton H (2001) “Introducción al Álgebra lineal” John Wiley and Sons (Traducido al español) § Capítulos 3 al 5 principalmente, pero aquí también puedes encontrar la SVD (Cap 7. ) § Lee, M. (2010) “Introduction to topological manifolds” Springer § …entrada amable, e incorpora una sección con el enlace al álgebra. © 2013 -6. Dr. Felipe Orihuela-Espina 3

VECTORES Y ESPACIOS VECTORIALES © 2013 -6. Dr. Felipe Orihuela-Espina 4

ESPACIOS Y CAMPOS VECTORIALES © 2013 -6. Dr. Felipe Orihuela-Espina 5

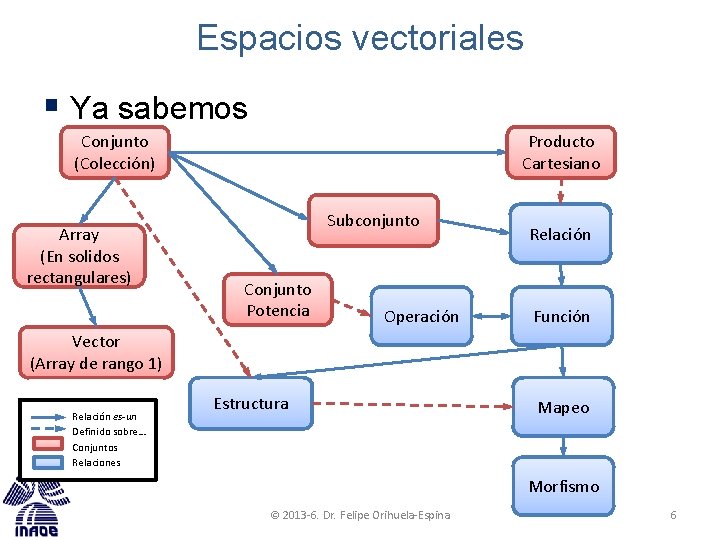
Espacios vectoriales § Ya sabemos Conjunto (Colección) Array (En solidos rectangulares) Producto Cartesiano Subconjunto Conjunto Potencia Operación Relación Función Vector (Array de rango 1) Relación es-un Definido sobre… Conjuntos Relaciones Estructura Mapeo Morfismo © 2013 -6. Dr. Felipe Orihuela-Espina 6

Espacios vectoriales § Espacio: Un conjunto X con una estructura añadida. § Espacio vectorial: Un conjunto X de arrays con las operaciones cerradas de suma vectorial y multiplicación escalar. § A menudo los elementos son vectores, pero podrían ser § § escalares, arrays, tensores, etc…a pesar del nombre La estructura impuesta sobre el conjunto del espacio vectorial corresponde a una estructura algebraica de tipo Campo; cumple la conmutativa, la asociativa, etc… Las operaciones suma vectorial y multiplicación escalar para vectores son casos particulares de las análogas para matrices. * Las definiciones formales las podéis encontrar en libros, o en Wolfram World of Maths [http: //mathworld. wolfram. com/] © 2013 -6. Dr. Felipe Orihuela-Espina 7

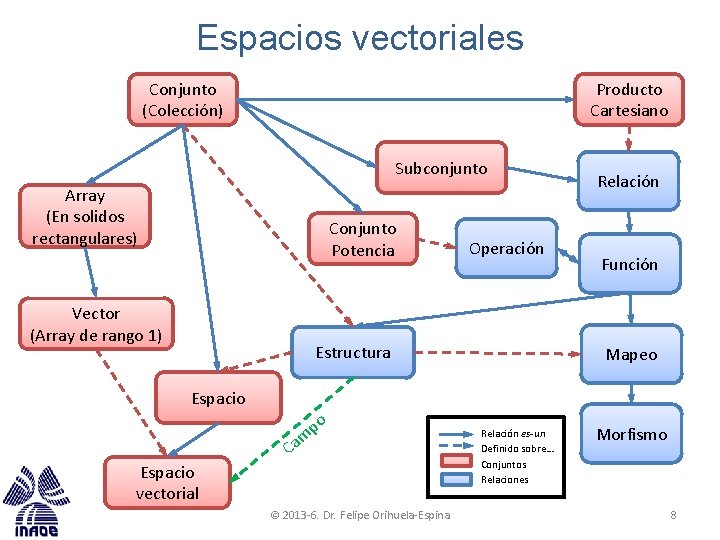
Espacios vectoriales Conjunto (Colección) Producto Cartesiano Subconjunto Array (En solidos rectangulares) Conjunto Potencia Vector (Array de rango 1) Operación Estructura Relación Función Mapeo Espacio po m Ca Espacio vectorial © 2013 -6. Dr. Felipe Orihuela-Espina Relación es-un Definido sobre… Conjuntos Relaciones Morfismo 8

Espacios vectoriales § Dimensión del espacio vectorial: § La dimensión del espacio vectorial es el máximo número de vectores linealmente independientes entre si. § …o sea el rango de la matriz correspondiente a “apilar” todos los vectores del conjunto subyacente. § La dimensión puede ser infinita. © 2013 -6. Dr. Felipe Orihuela-Espina 9

Espacios vectoriales § Orden del espacio vectorial: § El orden del espacio vectorial es la longitud u orden de los vectores. § NOTA: A menudo se usa el término dimensionalidad intrínseca para llamar a la dimensionalidad o rango, y simplemente dimensionalidad para referirse al orden, lo cual es ambiguo. § A menudo la dimensionalidad (dimensionalidad intrínseca) y § el orden (dimensionalidad) coinciden. Cuando este no es el caso, entonces se suele hacer explícita la diferencia, precisamente usando el término de dimensionalidad intrínseca. © 2013 -6. Dr. Felipe Orihuela-Espina 10

Espacios vectoriales § Subespacio vectorial: § Sea V un espacio vectorial, y sea W un subconjunto de V donde también se cumplen las operaciones (la estructura) de V. Entonces W es un subespacio vectorial y se denota W⊆V. § NOTA: Observa que la notación es similar a la de los conjuntos subyacentes al espacio, y de alguna forma “ignora” las operaciones. © 2013 -6. Dr. Felipe Orihuela-Espina 11

Espacios vectoriales § Conjunto de bases: § Sea V un espacio vectorial y G un conjunto de vectores. Si cada uno de los vectores v∈V se puede expresar como una combinación lineal de los elementos de G, entonces se dice que G es un conjunto generador. Se denota como V(G) o span(G). § Los elementos de G no tienen por que pertenecer a V. § …aunque si se me permite la osadía (y sin prueba ninguna) eso es como poco infrecuente. © 2013 -6. Dr. Felipe Orihuela-Espina 12

Espacios vectoriales § Conjunto de bases: § Si además los vectores de G son linealmente independientes entre si, entonces de dice que conforman una base de V. § Teorema: La representación de un vector dado en términos de una base es única. § Demostración: [Gentle 2007, pg 14] © 2013 -6. Dr. Felipe Orihuela-Espina 13

Espacios vectoriales § Conjunto de bases: § El número de vectores (cardinalidad) en un conjunto generador es al menos tan grande como la dimensión intrínseca del espacio vectorial. § dim(V(G))≤#G § El número de vectores (cardinalidad) en una base es igual a la dimensión intrínseca del espacio vectorial. § dim(V(B))=#B © 2013 -6. Dr. Felipe Orihuela-Espina 14

Espacios vectoriales § Producto punto: § Informal: Si entendemos un vector como el crecimiento en una determinada dirección, entonces el producto punto es el crecimiento direccional que un vector traslada a otro. § El producto punto es mucho más que una simple proyección geométrica § http: //betterexplained. com/articles/vector-calculusunderstanding-the-dot-product/ Figura de: [mathinsight. org] © 2013 -6. Dr. Felipe Orihuela-Espina 15

Espacios vectoriales § Producto punto, producto interno o producto escalar: § Formal: Sea el espacio vectorial V. El producto punto es un producto de dos vectores u, v∈V está definido como: § Donde xi e yi representan los diferentes elementos del vector. § NOTA: El anterior es realmente el producto punto, y es un tipo especial de producto interno. No obstante, el producto punto es el producto interno más común, y se le suele llamar producto interno por extensión, pero no es el único producto interno que puede definirse. © 2013 -6. Dr. Felipe Orihuela-Espina 16

Espacios vectoriales § Producto punto: § Propiedades: § u⋅0=0⋅u=0⋅0=0 § Conmutativa: u⋅v=v⋅u § Multipicación por un escalar: a(u⋅v)=au⋅v=u⋅av § Distributiva con respecto a la suma vectorial: (u+v)⋅t=u⋅t+v⋅t © 2013 -6. Dr. Felipe Orihuela-Espina 17

Espacios vectoriales § Norma: § Una norma, se denota como ||⋅||, es cualquier función que mapea un vector con un escalar y que satisfaga las siguientes condiciones: 1. No negatividad: x≠ 0 → ||x||≠ 0 2. Mapeo de la identidad: ||0||=0 3. Multiplicación por un escalar: ||ax||=a||x|| 4. Inequidad del triángulo: ||x+y||≤ ||x||+||y|| § Si se relaja alguna condición se llama § pseudonorma. Si se relajan las condiciones 1 y 2 se llama seminorma. © 2013 -6. Dr. Felipe Orihuela-Espina 18

Espacios vectoriales § NOTA: Una norma no es una métrica como tal; la norma está definida sobre un único elemento, mientras que una métrica está definida sobre dos elementos. Pero dicho eso, ambas funciones están íntimamente relacionadas. § A menudo, una métrica obvia es la norma de la diferencia. De hecho a esta se le llama la métrica inducida por la norma. © 2013 -6. Dr. Felipe Orihuela-Espina 19

Espacios vectoriales § Normas de Minkowski o Lp: § Sea p≥ 1, las normas de Minkowski o Lp se definen como: § donde |⋅| representa el módulo del elemento, y xi son los distintos elementos del vector x. © 2013 -6. Dr. Felipe Orihuela-Espina 20

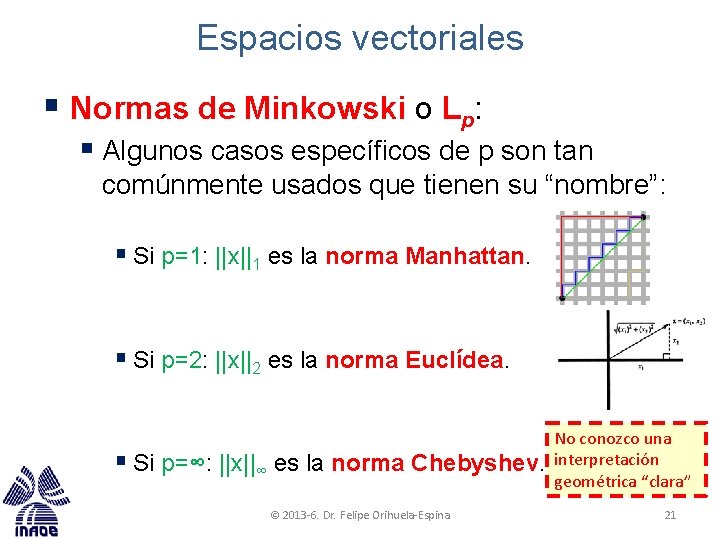
Espacios vectoriales § Normas de Minkowski o Lp: § Algunos casos específicos de p son tan comúnmente usados que tienen su “nombre”: § Si p=1: ||x||1 es la norma Manhattan. § Si p=2: ||x||2 es la norma Euclídea. § Si p=∞: ||x||∞ es la norma Chebyshev. © 2013 -6. Dr. Felipe Orihuela-Espina No conozco una interpretación geométrica “clara” 21

Espacios vectoriales § Normas de Minkowski o Lp: § Las normas de Minkowski son

Espacios vectoriales § Normas de Minkowski o Lp: § Existe una versión pesada: §

Espacios vectoriales § Normalización: § Hay distintas formas de normalización (ej: a un rango, a media=0 y var=1), pero un común es dividir por la norma: § …se dice entonces que el vector está normalizado. © 2013 -6. Dr. Felipe Orihuela-Espina 24

TOPOLOGÍA © 2013 -6. Dr. Felipe Orihuela-Espina 25

Topología § “Topology is the field of mathematics that formalizes and generalizes the intuitive notion of "continuous deformation" of objects” [Wikipedia: Discrete_mathematics] © 2013 -6. Dr. Felipe Orihuela-Espina 26

Espacio topológico § Espacio Euclidiano: § Un espacio euclidiano es un espacio donde se satisfacen los axiomas o postulados de Euclides: 1. Dados puntos, e puede trazar una recta (1 sóla dimensión y 1 sóla dirección) que los une. § ¡Tiene que ser recta, no curva! 2. Cualquier segmento puede prolongarse de manera 3. 4. 5. continua en cualquier sentido Se puede trazar una circunferencia con centro en cualquier punto y de cualquier radio Todos los ángulos rectos son congruentes. Si una recta al cortar a otras dos, forman ángulos internos menores a dos ángulos rectos, esas dos rectas prolongadas indefinidamente se cortan del lado en el que están los dos ángulos menores a los rectos. © 2013 -6. Dr. Felipe Orihuela-Espina 27

Espacio topológico Figura de: [http: //www. huffingtonpost. com/mauricio-garrido/lessons-from-non-euclidian-geometries-for-interfaith-dialogue_b_3403930. html] © 2013 -6. Dr. Felipe

Espacio topológico § Espacio topológico: § Un espacio topológico es un conjunto de puntos X={xi|i=1…n} con un conjunto de subconjuntos T={Sj={xi∈X}}⊆X que satisface los siguientes axiomas: § El conjunto vacio está en T: ∅∈T § El conjunto X está en T: X∈T § La unión de una colección finita de conjuntos de T también está en T: § La intersección de una colección arbitraria de conjuntos de T también está en T: © 2013 -6. Dr. Felipe Orihuela-Espina 29

Espacio topológico § Topología: § El conjunto X se conoce como el substrato del espacio topológico. § El conjunto T es la topología de X. § Básicamente, un espacio topológico es un cuerpo geométrico, y la topología es la estructura impuesta. © 2013 -6. Dr. Felipe Orihuela-Espina 30

Manifold § Variedad (Manifold): § Informal: Una variedad es un cuerpo geométrico. § Semi-Formal: Una variedad (manifold) es una espacio topológico que es localmente Euclidiano. § …o sea, que al menos visto de “cerca” o a pequeña escala, en una vecindad, cumple con los postulados Euclidianos. § El tamaño de la vecindad puede ser diferencial. © 2013 -6. Dr. Felipe Orihuela-Espina 31

Manifold § Variedad (Manifold): § Formal: Una variedad topológica es un espacio topológico en que cada punto tiene un entorno homeomorfo a un conjunto abierto de Rn. visto s o m e h o Aún n os. Lo m s i f r o m homeo n 1 veremos e segundo. © 2013 -6. Dr. Felipe Orihuela-Espina 32

Manifold § Variedad (Manifold): § Ejemplo: Figura de: [tvtropes. org] © 2013 -6. Dr.

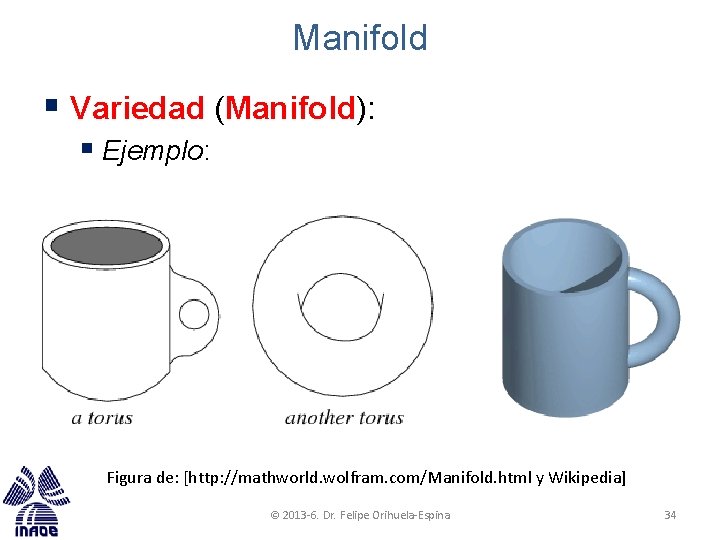
Manifold § Variedad (Manifold): § Ejemplo: Figura de: [http: //mathworld. wolfram. com/Manifold. html y

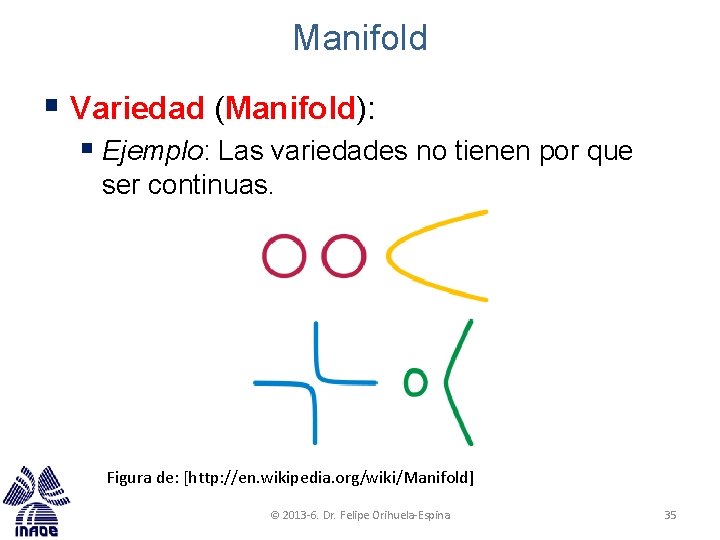
Manifold § Variedad (Manifold): § Ejemplo: Las variedades no tienen por que ser continuas.

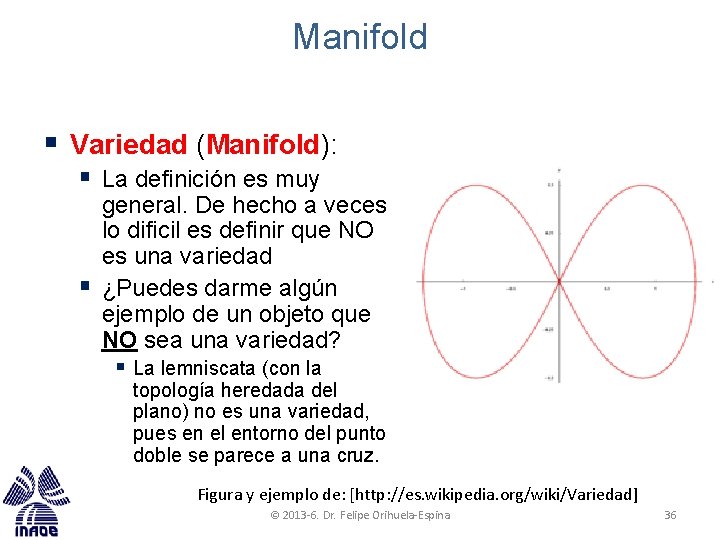
Manifold § Variedad (Manifold): § La definición es muy § general. De hecho a veces lo dificil es definir que NO es una variedad ¿Puedes darme algún ejemplo de un objeto que NO sea una variedad? § La lemniscata (con la topología heredada del plano) no es una variedad, pues en el entorno del punto doble se parece a una cruz. Figura y ejemplo de: [http: //es. wikipedia. org/wiki/Variedad] © 2013 -6. Dr. Felipe Orihuela-Espina 36

Manifold § Variedad (Manifold): § El concepto de variedad es la generalización del espacio Euclidiano tradicional para adaptarlo a topologías no Euclidianas. § Ser “localmente Euclidiano” no significa que esté restringido a la métrica Euclidiana de forma global. § Conceptualmente, una variedad es un objeto colocado en un espacio ambiente n-dimensional. § Por supuesto la variedad no tiene por que tener dimensión n. © 2013 -6. Dr. Felipe Orihuela-Espina 37

Manifold § Variedad (Manifold): § Si la variedad es infinitamente diferenciable se dice que es una variedad diferenciable (smooth manifold). § Un variedad diferenciable con una métrica impuesta para inducir la topología se llama una variedad de Riemannian. os m e h o n Aún ica r t é m o d i defin © 2013 -6. Dr. Felipe Orihuela-Espina 38

Manifold § Subvariedad (Submanifold): § Una subvariedad es un subconjunto de una variedad, que a su vez es una variedad. § Una variedad k-dimensional es una subvariedad con k grados de libertad, en otras palabras, puede ser descrito únicamente con k-coordenadas. § Ejemplo clásico: Una esfera es un objeto bidimensional en un espacio tridimensional. La esfera es una subvariedad 2 -dimensional. © 2013 -6. Dr. Felipe Orihuela-Espina 39

MORFISMOS © 2013 -6. Dr. Felipe Orihuela-Espina 40

Morfismos § Morfismos o homomorfismo: § Un homomorfismo o simplemente morfismo es una transformación entre espacios topológicos que preserva las estructuras. § …o sea, un mapeo entre espacios topológicos § Recuerda, preservar las estructuras significa que las operaciones que se cumplían en X se siguen cumpliendo en Y. © 2013 -6. Dr. Felipe Orihuela-Espina 41

Morfismos § Isomorfismo: § Un isomorfismo es un homomorfismo biyectivo. § El hecho de

Morfismos § Homeomorfismo*: § Sean dos espacios topológicos X e Y. Un homeomorfismo es una transformación entre X e Y que es continua y biyectiva. § El hecho de ser continua significa que dos puntos cercanos en X, también son cercanos en Y, y además, que los puntos lejanos en X también son lejanos en Y. *No confundir con homomorfismo. © 2013 -6. Dr. Felipe Orihuela-Espina 43

Morfismos § Difeomorfismo: § Un homeomorfismo que es diferenciable se llama un difeomorfismo. §

Morfismos § Embedding: (Proyección? ? - No se el término en español) § Un embedding es un mapeo f: X→Y tal que f es un difeomorfismo de X a Y, y f(Y) es una variedad diferenciable de f(X). § Un embedding es la representación de un objeto topológico (ej: una variedad, un grafo, un latice, etc) en un determinado (sub-)espacio de forma que se preserva la topología. § En particular, para variedades, preserva los conjuntos abiertos en T. § Si alguien quiere saber más: § Orihuela-Espina F “A tiny review on Manifold Embedding techniques” (Power. Point) © 2013 -6. Dr. Felipe Orihuela-Espina 45