Lezione n 9 Prof ssa Rossella Petreschi Lezione

Lezione n° 9 Prof. ssa Rossella Petreschi Lezione del 31/10/2014 del Corso di Algoritmica

Numeri di Catalano Il numero di alberi binari distinti con n nodi è pari al numero di Catalano di dimensione n: Cn = (2 n su n)/(n+1), risultato dell’equazione ricorsiva Cn = ∑ Cs Cn-s-1, con 0 ≤ s ≤ n-1 e C 0= C 1=1 C 2= 2 C 3= 5 C 4= 14 C 5= 42 ………….

Quanti bit per un albero binario? Per rappresentare un qualunque albero binario con n nodi occorrono un numero di bit pari a log Cn = log[(2 n su n)/ (n+1)] > > log[(22 n)/ (2 n(n+1))] per la (*) = 2 n - O(logn) (*) (2 n su n) = (2 n)!/n! (2 n-n)! = = (2 n/2 n) [2 n (2 n-1) (2 n-2)……. 1]/[n(n-1)(n-2)… 1]) = = (1/2 n)[(2 n 2 n)/(nn)][(2 n-1)(2 n-2)/(n-1)]… [3 x 2/1] > > (1/2 n)[(22 n 2/n 2)][(2 n-2)/(n-1)]… [2 x 2/1] = = (1/2 n) [22 n 2/n 2] [22(n-1)2 /(n-1)2]… [22/12] = (1/2 n) x (22 n)

Alberi k-ari e ordinali • alberi k-ari (o cardinali): ogni nodo ha k riferimenti ai figli, numerati da 0 a k (binari se da 0 a 2) • alberi ordinali: ogni nodo memorizza solamente la lista dei figli, variabile da nodo.

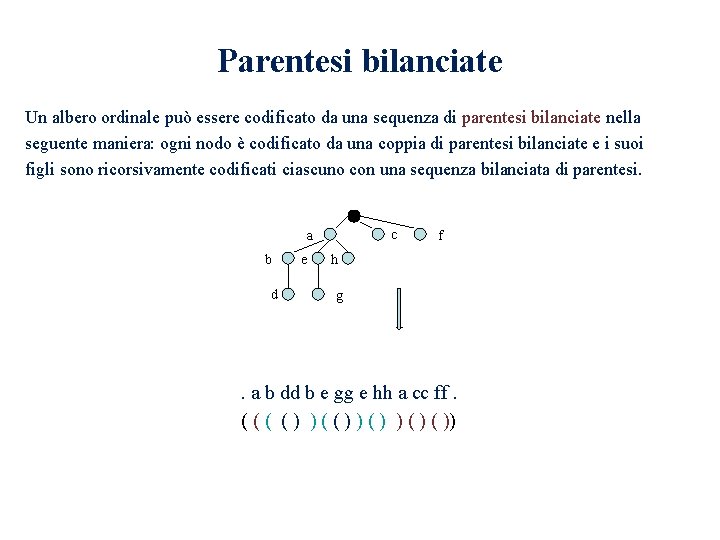
Parentesi bilanciate Un albero ordinale può essere codificato da una sequenza di parentesi bilanciate nella seguente maniera: ogni nodo è codificato da una coppia di parentesi bilanciate e i suoi figli sono ricorsivamente codificati ciascuno con una sequenza bilanciata di parentesi. c a b d e f h g . a b dd b e gg e hh a cc ff. ( ( ) ) ( ))

Corrispondenza biunivoca Esiste una corrispondenza biunivoca tra • Alberi binari (2 -ari) di n nodi; • Alberi ordinali di n+1 nodi ; • Sequenze bilanciate di 2 n parentesi E la cardinalità di questi tre insiemi è il numero di catalano di dimensione n : C n = (2 n su n)/(n+1) a b c d e g c a b f d e f h g h . a b dd b e gg e hh a cc ff. ((( () )())()()) NOTA: non si possono rappresentare direttamente alberi binari mediante parentesi perché non c’è modo di distinguere fs da fd

Come rappresentare un albero binario Consideriamo che per ogni nodo u sia data la rappresentazione compressa del propria informazione u-info, quindi ci soffermiamo su come rappresentare le relazioni fra i nodi, ovvero su come rappresentare u-padre, u-fs e u-fd. Rappresentazione implicita: mantiene u-padre, u-fs e u-fd tramite una semplice regola matematica senza uso di memoria aggiuntiva. Esempio: rappresentazione dell’heap Utilizzabile solo per alcune classi di alberi binari Se pensiamo ad alberi binari qualunque, abbiamo: Rappresentazione esplicita: rappresentazione che impiega per ogni nodo u un numero di bits almeno pari a 3 logn, dato che logn è il numero minimo di bits necessari per rappresentare un qualunque nodo. Rappresentazione succinta: rappresentazione che usa per rappresentare le relazioni fra i nodi dell’albero strutture dati che richiedono un totale di 2 n + o(n) bits, ovvero una quantità di memoria pari a quanto si è dimostrato essere il minimo necessario.

Rappresentazione succinta per ampiezza a b c d e abcdef 1110100110000 nodo[0, …, n-1] pieno[0, …, 2 n] f • Se un nodo occupa la posizione i nell’array nodo, allora i bit corrispondenti ai suoi due figli occupano le posizioni 2 i+1 e 2 i+2 nell’array pieno • Se un nodo occupa la posizione i nell’array nodo, allora pieno[2 i+1]=1(pieno[ 2 i+2]=1) iff il riferimento al fs (fd) non è null Oltre all’array nodo, dobbiamo conteggiare 2 n+1 bits necessari per l’array pieno + lo spazio per navigare fra i due array, mantenendo tempo costante

Come navigare: Rank, Select abcdef a b nodo[0, …, n-1] d e 1110100110000 pieno[0, …, 2 n]; c • Rank(pieno, i): numero di 1 presenti nel segmento pieno[0, i] 0<=i<=2 n f • Select(pieno, i): posizione dell’(i+1)-esimo 1 in pieno 0<=i<=Rank(pieno, 2 n) Identificazione in nodo[] del fs(nodo[i]) o del fd(nodo[i]) : f = 2 i+1 (o d = 2 i+2 ): posizione del fs (o fd) di i in pieno[]; Se pieno(f) non 0 (o pieno(d) non 0), Rank(pieno, f (oppure d)): numero di 1 presenti nel segmento pieno[0, f]opure pieno[0, d]; nodo[Rank(pieno, f (oppure d)) -1]: fs[nodo(i)] oppure fd[nodo(i)]. Identificazione in nodo[] del padre(nodo[i]): p = Select (pieno, i): bit 1 corrispondente a nodo[i] in pieno[]; nodo(p-1)/2: padre[nodo(i)].