Lezione 7 Effetto Compton Francesco Adduci Fisica Atomica

Lezione 7 Effetto Compton Francesco Adduci Fisica Atomica e Molecolare 1

Testo di riferimento Eisberg & Resnick Quantum Physics of Atoms, Molecules, Solids, Nuclei, ad Particles CD lezione 7 Francesco Adduci Fisica Atomica e Molecolare 2

L’effetto Compton Arthur Holly Compton (Wooster, Ohio, 1892 † Berkeley, California, 1962) Primo premio Nobel americano, per la fisica (1927). Francesco Adduci Fisica Atomica e Molecolare 3

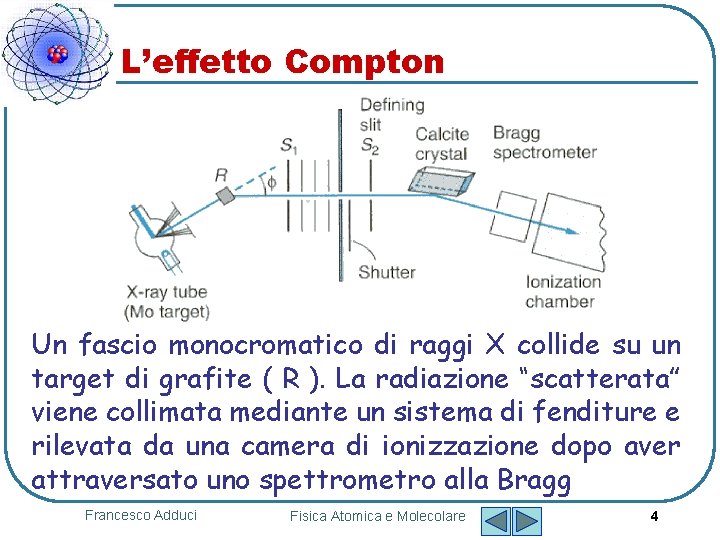
L’effetto Compton Un fascio monocromatico di raggi X collide su un target di grafite ( R ). La radiazione “scatterata” viene collimata mediante un sistema di fenditure e rilevata da una camera di ionizzazione dopo aver attraversato uno spettrometro alla Bragg Francesco Adduci Fisica Atomica e Molecolare 4

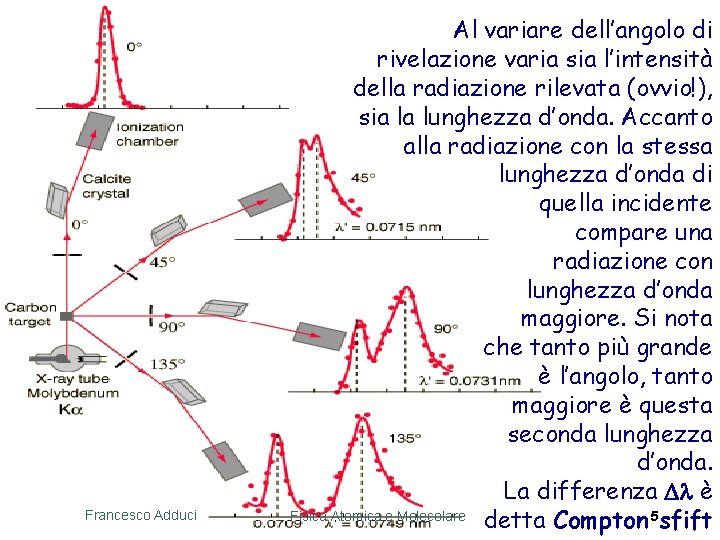
Francesco Adduci Al variare dell’angolo di rivelazione varia sia l’intensità della radiazione rilevata (ovvio!), sia la lunghezza d’onda. Accanto alla radiazione con la stessa lunghezza d’onda di quella incidente compare una radiazione con lunghezza d’onda maggiore. Si nota che tanto più grande è l’angolo, tanto maggiore è questa seconda lunghezza d’onda. La differenza D è Fisica Atomica e Molecolare detta Compton 5 sfift

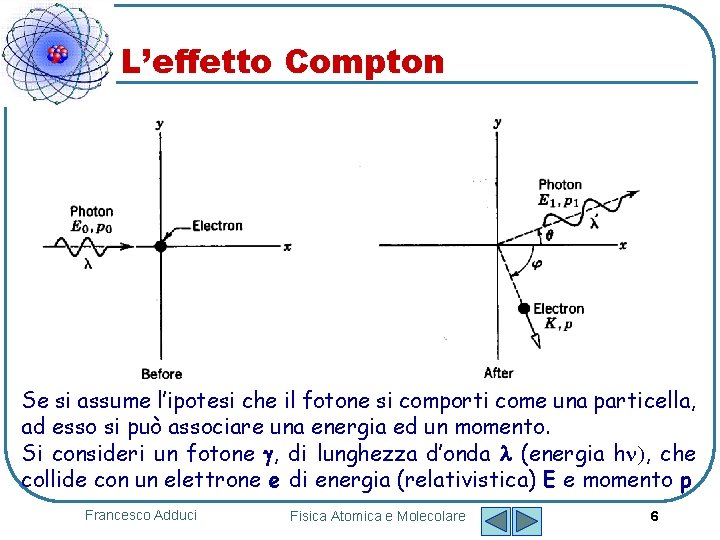
L’effetto Compton Se si assume l’ipotesi che il fotone si comporti come una particella, ad esso si può associare una energia ed un momento. Si consideri un fotone , di lunghezza d’onda (energia hn), che collide con un elettrone e di energia (relativistica) E e momento p Francesco Adduci Fisica Atomica e Molecolare 6

L’effetto Compton (Tutte le grandezze relative ad istanti successivi alla collisione sono indicate con un apice) Supponiamo che il fotone prosegua in una direzione che forma un certo angolo con quella di incidenza. Per la conservazione della quantità di moto o momento si ha: (1) e (2) Francesco Adduci Fisica Atomica e Molecolare 7

L’effetto Compton ma (3) (4) Sostituendo le (3) e (4) in (2) si ottiene (5) Francesco Adduci Fisica Atomica e Molecolare 8

L’effetto Compton Per la conservazione dell’energia si ha (6) e Poichè (7) Francesco Adduci Fisica Atomica e Molecolare 9

L’effetto Compton Si ottiene (8) da cui (9) Uguagliando la (5) e la (9) si ha Francesco Adduci Fisica Atomica e Molecolare 10

L’effetto Compton riscrivendo Francesco Adduci Fisica Atomica e Molecolare 11

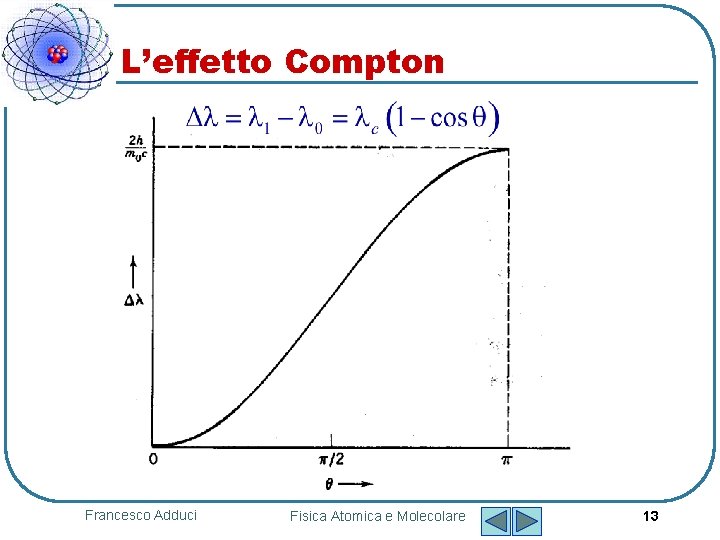
L’effetto Compton Si può anche scrivere: dove C=h/mc è nota come lunghezza d’onda di Compton N. B. dipende solo da e non da ! Francesco Adduci Fisica Atomica e Molecolare 12

L’effetto Compton Francesco Adduci Fisica Atomica e Molecolare 13

L’effetto Compton In una serie di esperimenti successivi fu verificata la simultanea espulsione dell’elettrone emisurata lasuaenergia. I risultati sperimentali confermarono la spiegazione dell’effetto Compton Francesco Adduci Fisica Atomica e Molecolare 14

L’effetto Compton Il picco a Θ=0 corrisponde alla lunghezza d’onda incidente. Nella spiegazione si ipotizza che gli elettroni con cui collidono i raggi X siano liberi. Tuttavia è anche possibile che un elettrone sia legato fortemente. In tal caso l’effettiva collisione avviene non solo con la sua massa (m 0) ma con quella dell’intero atomo (M~22, 000 m 0 per il carbonio). In queste nuove condizioni la lo shift Compton sarà: In pratica non si potrà misurare nessuno shift Francesco Adduci Fisica Atomica e Molecolare 15

L’effetto Compton Può anche accadere che lo scattering avvenga tra fotone e nucleo. Anche in questo caso lo shift Compton è troppo piccolo (rispetto ad un valore tipico di radiazione X) per essere misurato. Ma se il fotone invece di essere un X è un g con lunghezza d’onda tipica di 10 -3 Å ritorna la possibilità di apprezzare lo shift Da modificare Francesco Adduci Fisica Atomica e Molecolare 16

Lo scattering Raleigh Un altro modo di interazione tra radiazione e materia è quello conosciuto con il nome di scattering Raleigh, la cui caratteristica principale è quella che la radiazione scatterata ha esclusivamente la lunghezza d’onda della radiazione incidente. Intorno al 1900 Raleigh, ipotizzò che una radiazione elettromagnetica fosse in grado di far vibrare gli elettroni alla stessa frequenza della radiazione incidente, generando così una nuova radiazione della stessa lunghezza d’onda emessa in altra direzione qualsiasi. Lo scattering Raleigh predomina nella regione spettrale che va dalle onde radio al visibile, mentre lo scattering Compton prevale per fotoni X e . In realtà se accadesse uno scattering Compton non sarebbe misurabile, mentre nella zona diventa prevalente la produzione di coppia rispetto allo scattering Compton Francesco Adduci Fisica Atomica e Molecolare 17

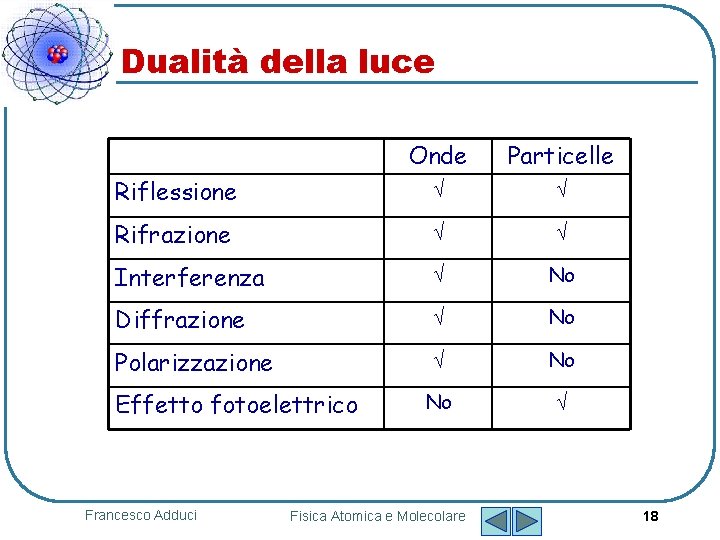
Dualità della luce Onde Particelle Riflessione Ö Ö Rifrazione Ö Ö Interferenza Ö No Diffrazione Ö No Polarizzazione Ö No No Ö Effetto fotoelettrico Francesco Adduci Fisica Atomica e Molecolare 18