Ley de Ampere Una corriente elctrica y su

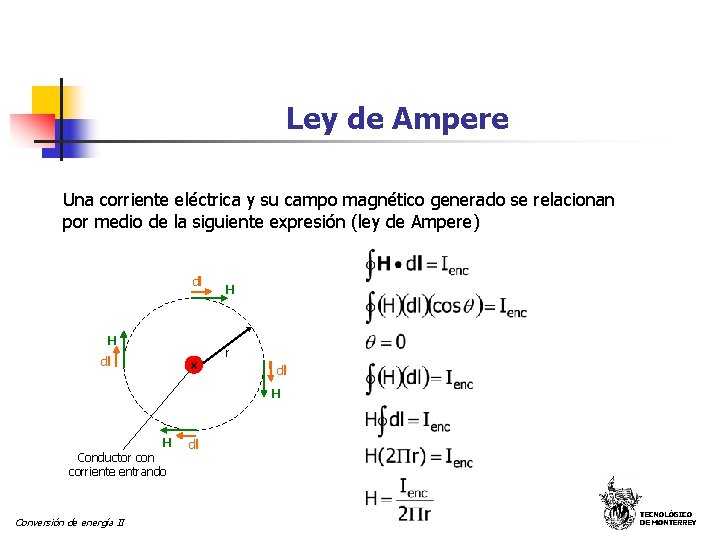
Ley de Ampere Una corriente eléctrica y su campo magnético generado se relacionan por medio de la siguiente expresión (ley de Ampere) H vector intendidad de campo magnético (A/m) dl vector diferencial de longitud a lo largo de la trayectoria de integración (M) Ienc corriente encerrada por la trayectoria de integración (A) Conversión de energía II TECNOLÓGICO DE MONTERREY

Ley de Ampere Una corriente eléctrica y su campo magnético generado se relacionan por medio de la siguiente expresión (ley de Ampere) dl H dl x H r dl H H Conductor con corriente entrando Conversión de energía II dl TECNOLÓGICO DE MONTERREY

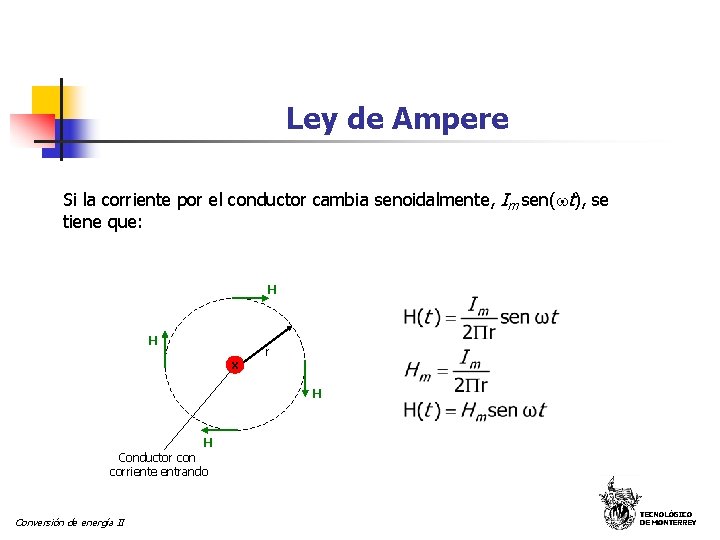
Ley de Ampere Si la corriente por el conductor cambia senoidalmente, Im sen( t), se tiene que: H H x r H H Conductor con corriente entrando Conversión de energía II TECNOLÓGICO DE MONTERREY

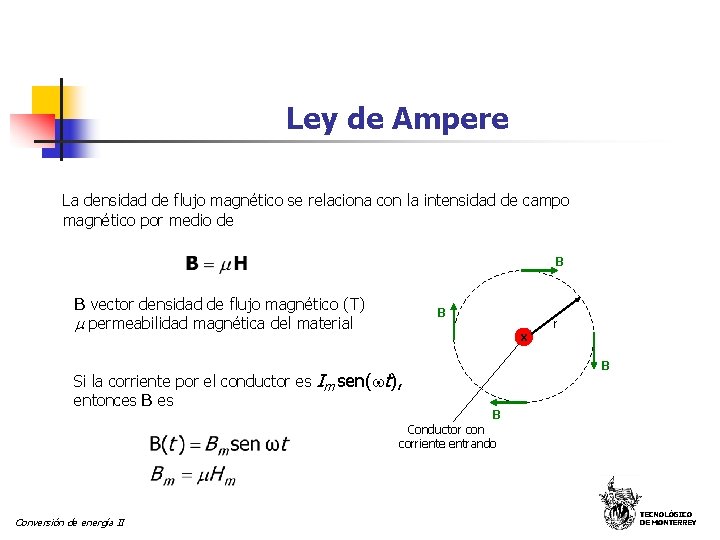
Ley de Ampere La densidad de flujo magnético se relaciona con la intensidad de campo magnético por medio de B B vector densidad de flujo magnético (T) permeabilidad magnética del material B x Si la corriente por el conductor es Im sen( t), entonces B es r B B Conductor con corriente entrando Conversión de energía II TECNOLÓGICO DE MONTERREY

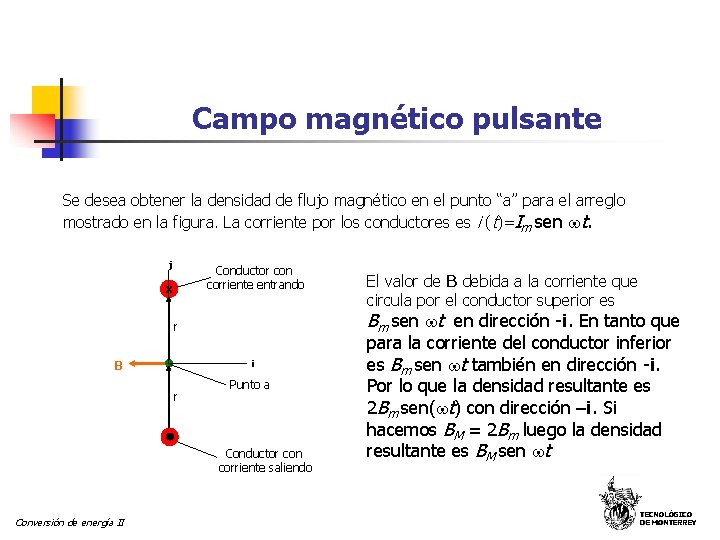
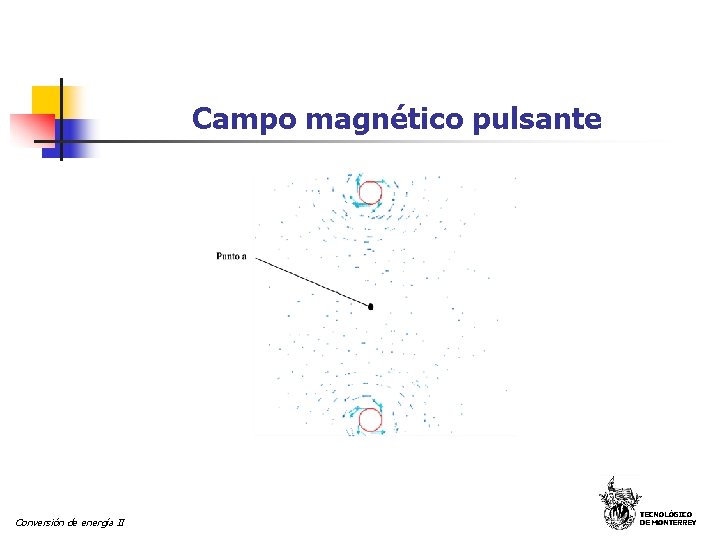
Campo magnético pulsante Se desea obtener la densidad de flujo magnético en el punto “a” para el arreglo mostrado en la figura. La corriente por los conductores es i (t)=Im sen t. j Conductor con corriente entrando x Bm sen t en dirección -i. En tanto que r i B r Punto a Conductor con corriente saliendo Conversión de energía II El valor de B debida a la corriente que circula por el conductor superior es para la corriente del conductor inferior es Bm sen t también en dirección -i. Por lo que la densidad resultante es 2 Bm sen( t) con dirección –i. Si hacemos BM = 2 Bm luego la densidad resultante es BM sen t TECNOLÓGICO DE MONTERREY

Campo magnético pulsante Conversión de energía II TECNOLÓGICO DE MONTERREY

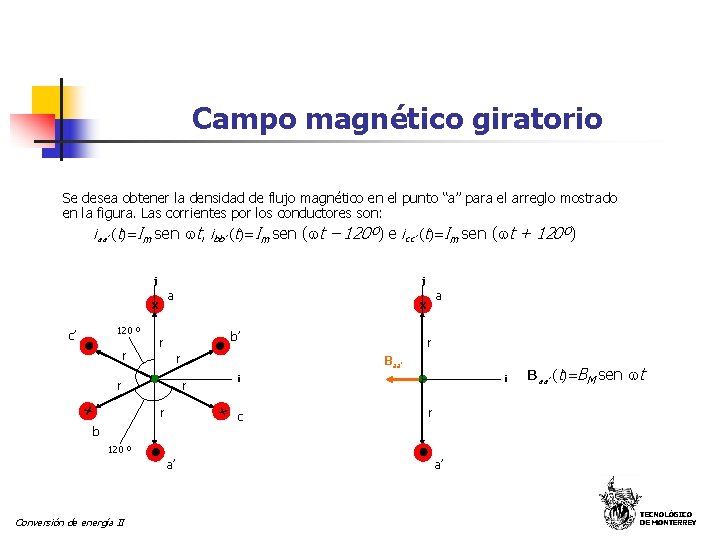
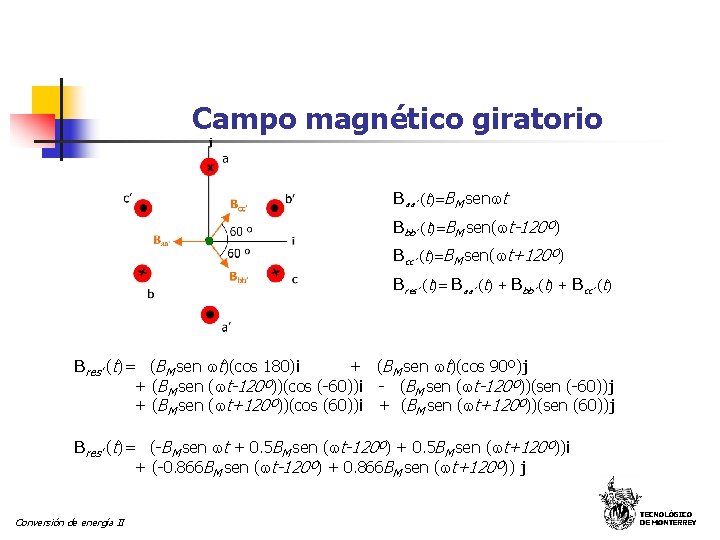
Campo magnético giratorio Se desea obtener la densidad de flujo magnético en el punto “a” para el arreglo mostrado en la figura. Las corrientes por los conductores son: iaa’ (t)=Im sen t, ibb’ (t)=Im sen ( t – 120º) e icc’ (t)=Im sen ( t + 120º) j j a x 120 º c’ r b’ r r i x x r r Baa’ r r a x c i Baa’ (t)=BM sen t r b 120 º a’ Conversión de energía II a’ TECNOLÓGICO DE MONTERREY

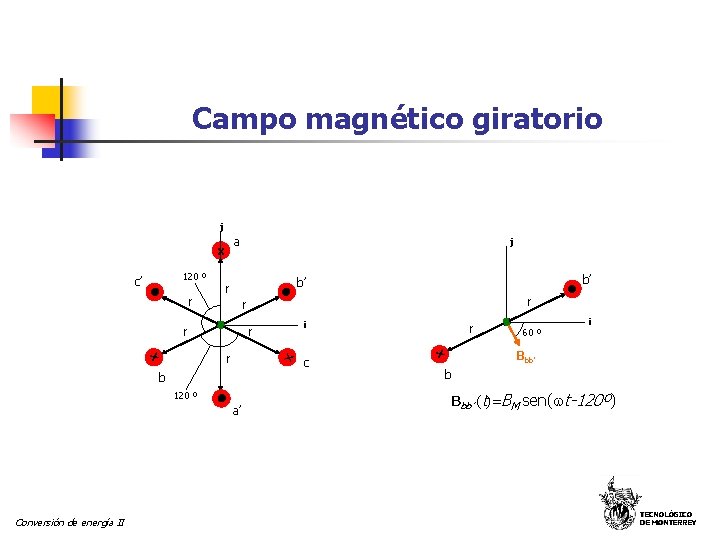
Campo magnético giratorio j a x 120 º c’ r r r i r r x x r x b’ b’ r r b 120 º a’ Conversión de energía II j c 60 º i Bbb’ b Bbb’ (t)=BM sen( t-120º) TECNOLÓGICO DE MONTERREY

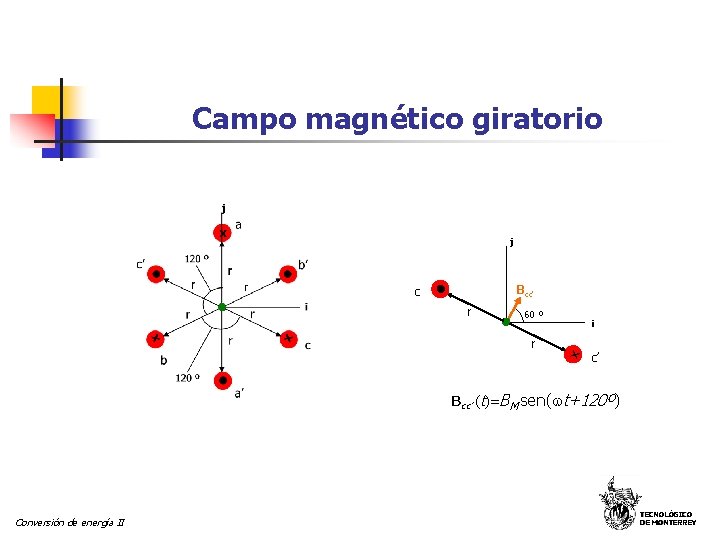
Campo magnético giratorio j Bcc’ c r 60 º i x r c’ Bcc’ (t)=BM sen( t+120º) Conversión de energía II TECNOLÓGICO DE MONTERREY

Campo magnético giratorio Baa’ (t)=BM sen t Bbb’ (t)=BM sen( t-120º) Bcc’ (t)=BM sen( t+120º) Bres’ (t)= Baa’ (t) + Bbb’ (t) + Bcc’ (t) Bres’ (t)= (BM sen t)(cos 180)i + (BM sen t)(cos 90º)j + (BM sen ( t-120º))(cos (-60))i - (BM sen ( t-120º))(sen (-60))j + (BM sen ( t+120º))(cos (60))i + (BM sen ( t+120º))(sen (60))j Bres’ (t)= (-BM sen t + 0. 5 BM sen ( t-120º) + 0. 5 BM sen ( t+120º))i + (-0. 866 BM sen ( t-120º) + 0. 866 BM sen ( t+120º)) j Conversión de energía II TECNOLÓGICO DE MONTERREY

Campo magnético giratorio Bres’ (t)= (-BM sen t + 0. 5 BM sen( t-120º) + 0. 5 BM sen( t+120º))i + (-0. 866 BM sen( t-120º) + 0. 866 BM sen( t+120º)) j Usando sen(A+B)= (sen A)(cos B) + (cos A)(sen B) Bres’ (t)= (-BM sen t + 0. 5 BM ((sen t)(cos 120º )- (cos t)(sen 120º )) + 0. 5 BM ((sen t)(cos 120º )+ (cos t)(sen 120º )) )i + (-0. 866 BM ((sen t)(cos 120º)- (cos t)(sen 120º)) + 0. 866 BM ((sen t)(cos 120º)+ (cos t)(sen 120º))) j Bres’ (t)= (-BM sen( t) + BM ((sen t)(cos 120º )))i + (1. 732 BM ((cos t)(sen 120º)))j Bres’ (t)= (-1. 5 BM sen( t))i + (1. 5 BM cos t)j Conversión de energía II TECNOLÓGICO DE MONTERREY

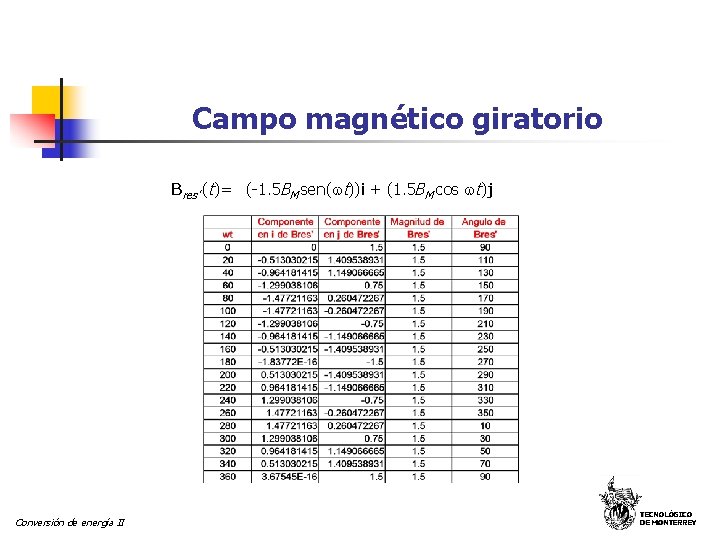
Campo magnético giratorio Bres’ (t)= (-1. 5 BM sen( t))i + (1. 5 BM cos t)j Conversión de energía II TECNOLÓGICO DE MONTERREY

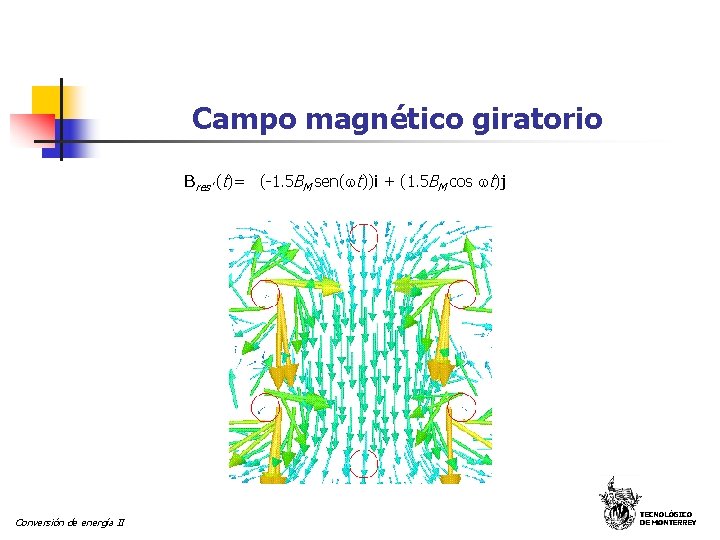
Campo magnético giratorio Bres’ (t)= (-1. 5 BM sen( t))i + (1. 5 BM cos t)j Conversión de energía II TECNOLÓGICO DE MONTERREY