Leveraging Recosting for Online Optimization of Parameterized Queries

Leveraging Re-costing for Online Optimization of Parameterized Queries Anshuman Dutt Joint work with Vivek Narasayya, Surajit Chaudhuri Microsoft Research

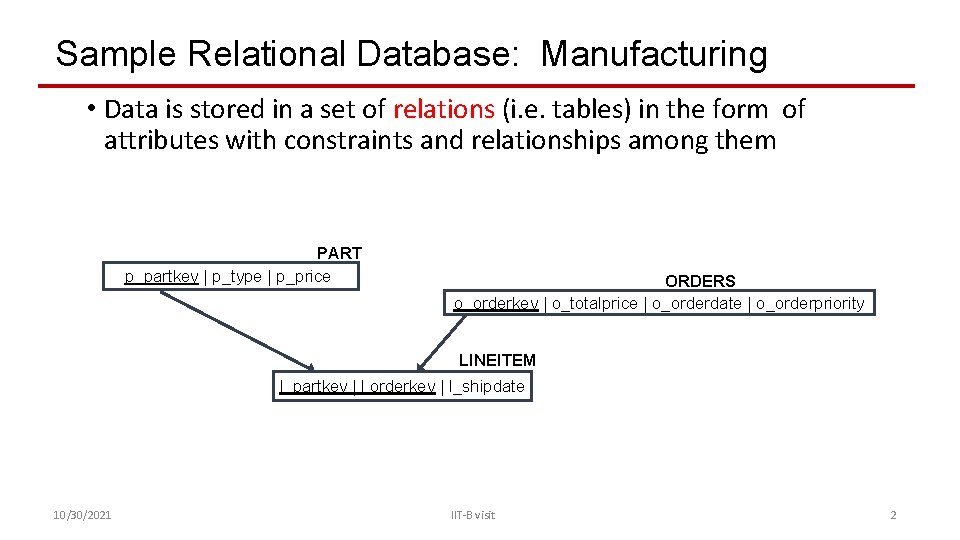
Sample Relational Database: Manufacturing • Data is stored in a set of relations (i. e. tables) in the form of attributes with constraints and relationships among them PART p_partkey | p_type | p_price ORDERS o_orderkey | o_totalprice | o_orderdate | o_orderpriority LINEITEM l_partkey | l orderkey | l_shipdate 10/30/2021 IIT-B visit 2

Query Interface • DECLARATIVE ACCESS • state what you want, not how to get it • unlike standard (imperative) programming, where you specify every step Declarative Example Query (EQ): Enumerate high priority orders for cheap parts select * from lineitem, orders, part where p_partkey = l_partkey and o_orderkey = l_orderkey and p_price < 1000 and o_orderpriority = ‘HIGH’ Unspecified: Join order [((O L) P) or ((P L) O) …] Join technique [Nested-Loops or Hash. Join …] 10/30/2021 IIT-B visit 3

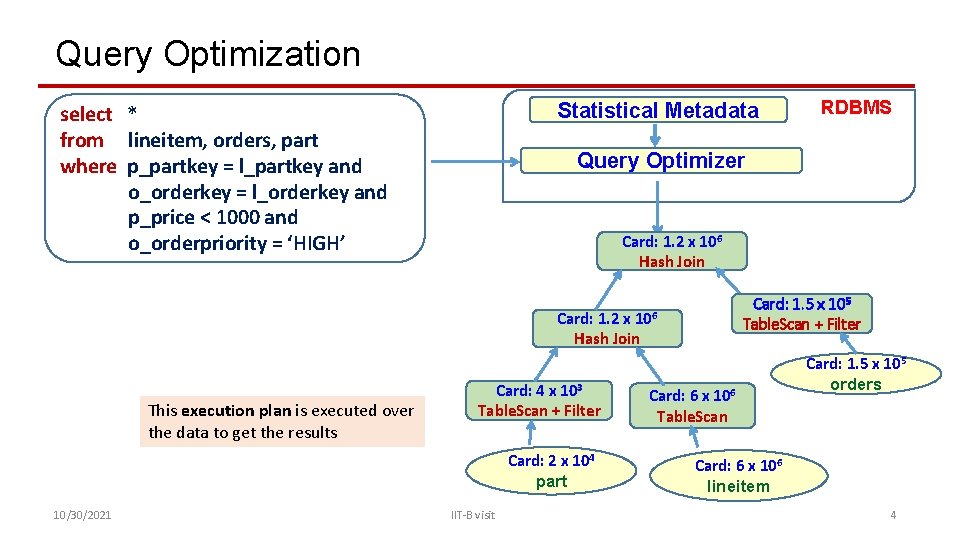
Query Optimization Statistical Metadata select * from lineitem, orders, part where p_partkey = l_partkey and o_orderkey = l_orderkey and p_price < 1000 and o_orderpriority = ‘HIGH’ Query Optimizer Card: 1. 2 x 106 Hash Join Card: 1. 5 x 105 Table. Scan + Filter 106 Card: 1. 2 x Hash Join This execution plan is executed over the data to get the results Card: 4 x 103 Table. Scan + Filter Card: 2 x 104 part 10/30/2021 RDBMS IIT-B visit Card: 6 x 106 Table. Scan Card: 1. 5 x 105 orders Card: 6 x 106 lineitem 4

Query as seen by optimizer Query optimizer cares about predicate selectivities (not parameter values) to determine optimal plan Selectivity = fraction of input tuples that satisfy the predicate qi (xi, yi) Sel 2 Selectivity (p_price < 1000) = xi ϵ [0, 1] Selectivity ( o_orderpriority = ‘HIGH’) = yi ϵ [0, 1] Sel 1 10/30/2021 IIT-B visit 5

Parameterized queries Example parameterized query Query instance 1 select * from lineitem, orders, part where p_partkey = l_partkey and Query instance 2 o_orderkey = l_orderkey and p_price < @Param 1 and @Param 1 = 100 @Param 2 = ’LOW’ @Param 1 = 10000 @Param 2 = ’MEDIUM’ o_orderpriority = @Param 2 Query instance 3 10/30/2021 IIT-B visit @Param 1 = 3000 @Param 2 = ’HIGH’ 6

Query Workload 20 19 Selectivity 2 18 5 10 13 Parametric Query Optimization 3 (term coined in early 1990 s) 17 4 1 12 11 14 7 15 8 2 6 16 9 Selectivity 1 10/30/2021 IIT-B visit 7

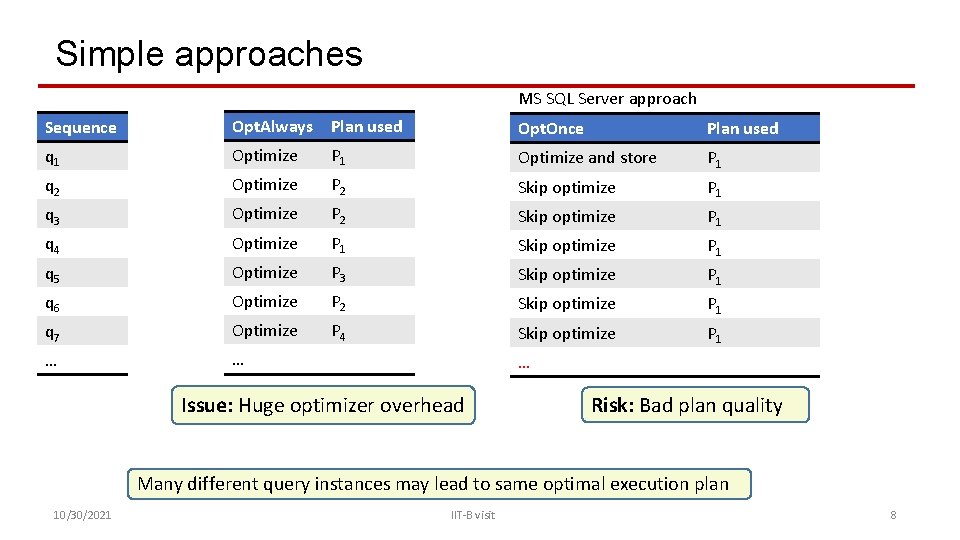
Simple approaches MS SQL Server approach Sequence Opt. Always Plan used Opt. Once Plan used q 1 Optimize P 1 Optimize and store P 1 q 2 Optimize P 2 Skip optimize P 1 q 3 Optimize P 2 Skip optimize P 1 q 4 Optimize P 1 Skip optimize P 1 q 5 Optimize P 3 Skip optimize P 1 q 6 Optimize P 2 Skip optimize P 1 q 7 Optimize P 4 Skip optimize P 1 … … … Issue: Huge optimizer overhead Risk: Bad plan quality Many different query instances may lead to same optimal execution plan 10/30/2021 IIT-B visit 8

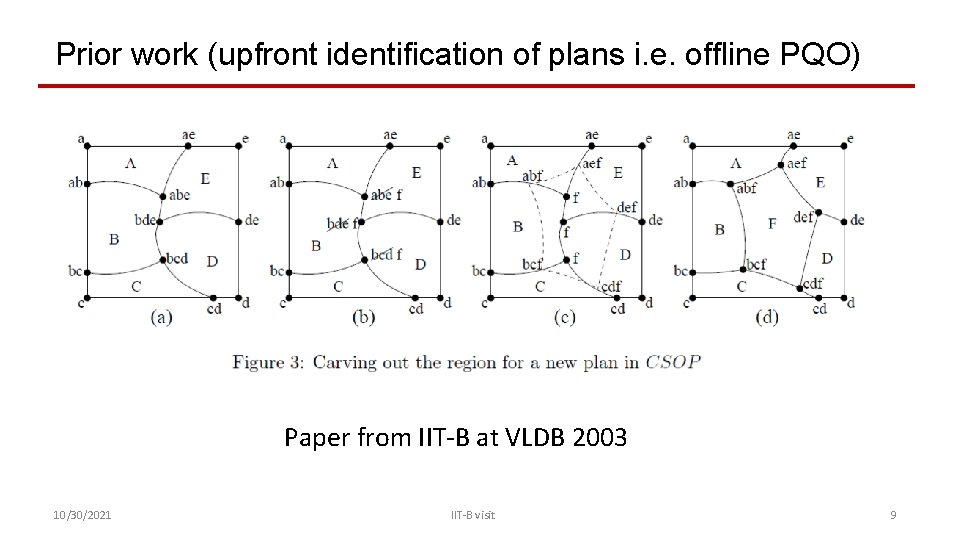
Prior work (upfront identification of plans i. e. offline PQO) Paper from IIT-B at VLDB 2003 10/30/2021 IIT-B visit 9

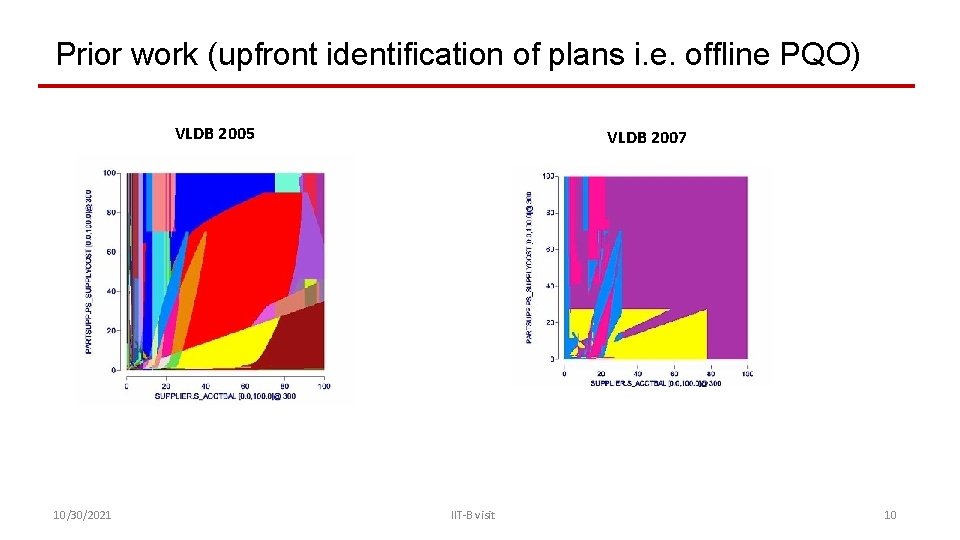
Prior work (upfront identification of plans i. e. offline PQO) VLDB 2005 10/30/2021 VLDB 2007 IIT-B visit 10

Performance Metrics (online PQO) • 10/30/2021 IIT-B visit 11

Competing factors and Goal Plan quality Worst 1, 0 E+4 [CELLREF ] Opt. Always Best 1, 0 E+3 -50 0 50 Optimize calls (%) 100 Goal: plan quality comparable to Opt. Always with significantly fewer optimize calls 10/30/2021 IIT-B visit Paper provides ways to keep number of plans under control (briefly hinted at the end of the talk) 12

Prior work 1: online PQO [VLDB 2008] Merging Ranges • Assumption • plan is close-to-optimal in a hypercube shaped selectivity region P 2 P 1 Sel 2 P 1 • Same plan found again • merge the selectivity ranges • Advantage P 3 P 1 P 4 Sel 1 10/30/2021 • skip many optimizer calls • Limitations • may choose sub-optimal plan • cannot discard a new plan in principled manner IIT-B visit 13

Prior work 2: online PQO [TKDE 2009] • Basis: Plan Cost Monotonicity • Plan cost increases with increase in selectivities • Ensures bounded sub-optimality of selected plan P 1, 500 q 1 new Sel 2 P 3, 100 q 3 10/30/2021 Sel 1 Candidate for selection : P 1 Cost sub-optimality < 5 (500/100) IIT-B visit : 14

Prior techniques: online PQO Bounded-PPQO [TKDE’ 09] (using assumption on plan cost behavior) Bounded cost sub -optimality Low optimizer overhead Cost sub-optimality Merging-Ranges [VLDB’ 08] Ellipse-PPQO [TKDE’ 09] Density based clustering [ICDE’ 12] -50 10/30/2021 1, 0 E+4 Merging Ranges [CELLREF ] Bounded-PPQO 1, 0 E+3 0 50 Optimize calls (%) IIT-B visit Opt. Always 100 15

Generic argument for online PQO • Needs optimize call P 1, 500 q 1 new Sel 2 P 3, 100 q 3 Sel 1 10/30/2021 IIT-B visit 16

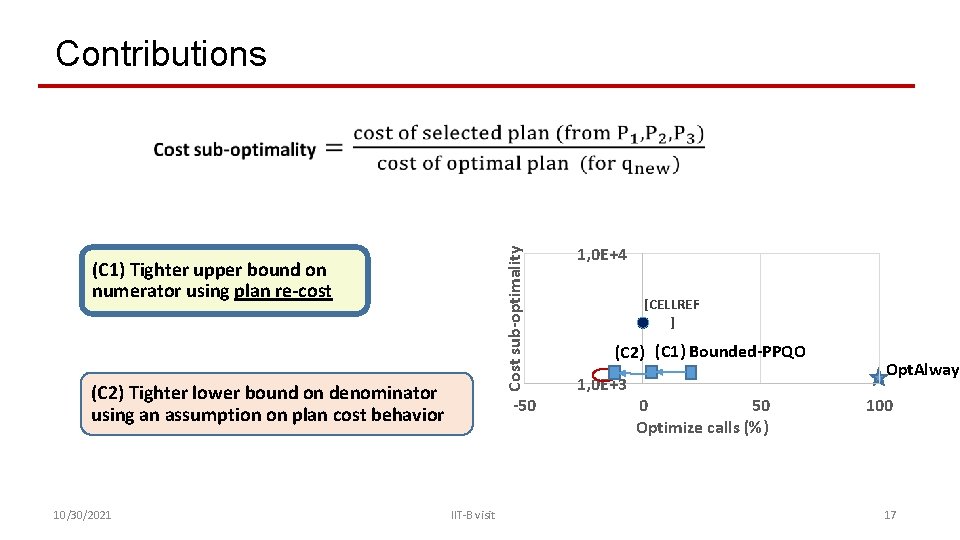
Cost sub-optimality Contributions (C 1) Tighter upper bound on numerator using plan re-cost (C 2) Tighter lower bound on denominator using an assumption on plan cost behavior 10/30/2021 -50 IIT-B visit 1, 0 E+4 [CELLREF ] (C 2) (C 1) Bounded-PPQO 1, 0 E+3 0 50 Optimize calls (%) Opt. Always 100 17

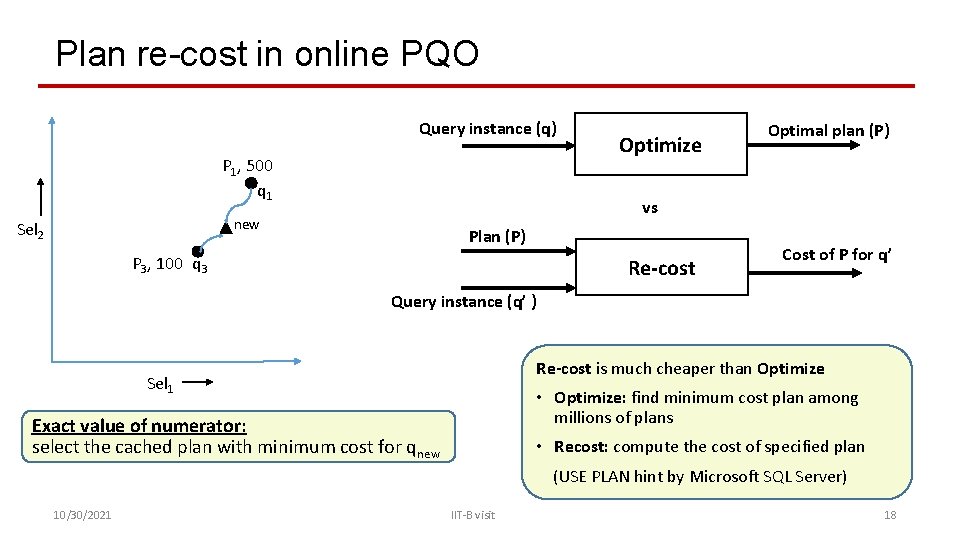
Plan re-cost in online PQO Query instance (q) P 1, 500 q 1 vs new Sel 2 Optimize Optimal plan (P) P 3, 100 q 3 Re-cost Cost of P for q’ Query instance (q’ ) Re-cost is much cheaper than Optimize Sel 1 • Optimize: find minimum cost plan among millions of plans Exact value of numerator: select the cached plan with minimum cost for qnew • Recost: compute the cost of specified plan (USE PLAN hint by Microsoft SQL Server) 10/30/2021 IIT-B visit 18

Advantages of plan re-costing in online PQO • Plan re-cost • can help significantly in terms of plan selection • can help any prior technique • This approach is very efficient when • number of plans is small • Re-cost itself helps to ensure small number of plans (shown in paper) 10/30/2021 IIT-B visit 19

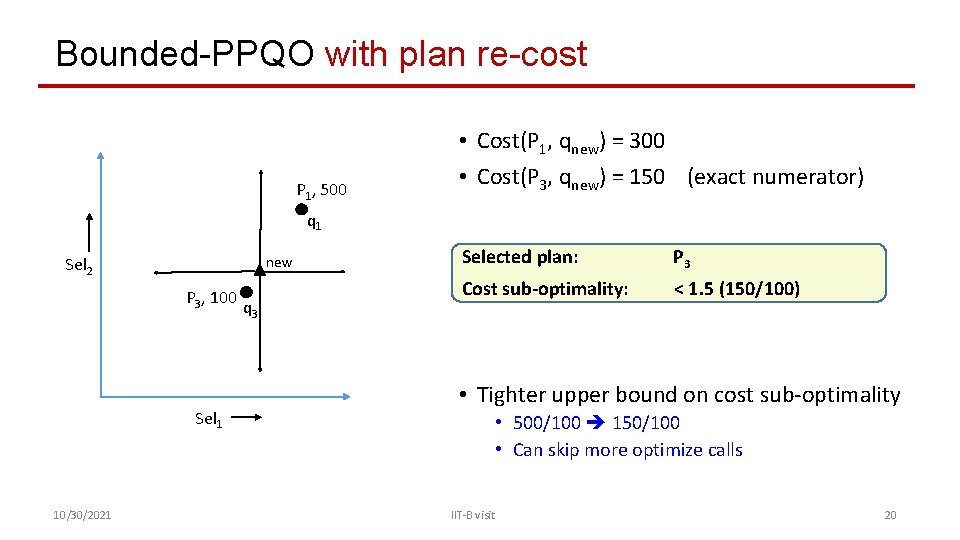
Bounded-PPQO with plan re-cost P 1, 500 • Cost(P 1, qnew) = 300 • Cost(P 3, qnew) = 150 (exact numerator) q 1 new Sel 2 P 3, 100 Sel 1 10/30/2021 q 3 Selected plan: P 3 Cost sub-optimality: < 1. 5 (150/100) • Tighter upper bound on cost sub-optimality • 500/100 150/100 • Can skip more optimize calls IIT-B visit 20

Contribution 2 Tighter lower bound on optimal cost (denominator)

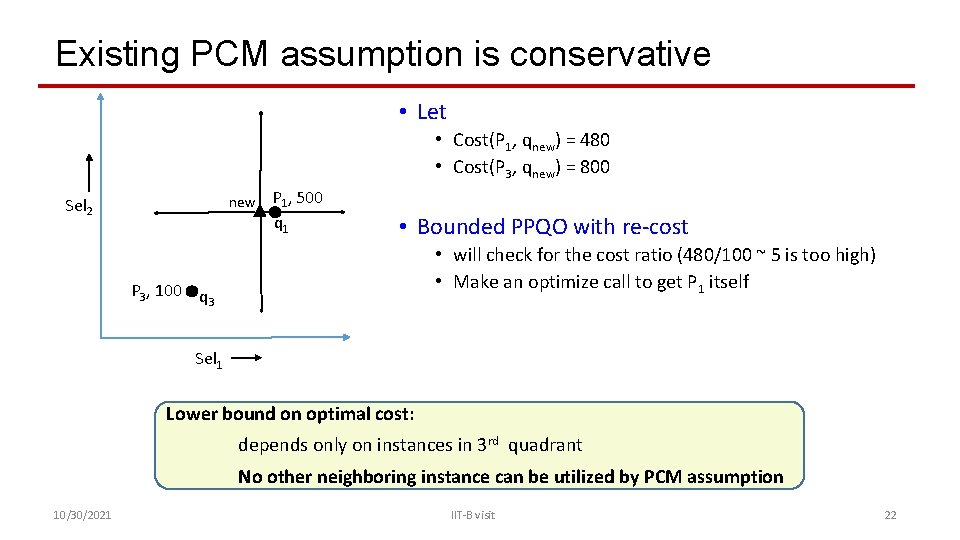
Existing PCM assumption is conservative • Let • Cost(P 1, qnew) = 480 • Cost(P 3, qnew) = 800 new Sel 2 P 1, 500 q 1 • Bounded PPQO with re-cost • will check for the cost ratio (480/100 ~ 5 is too high) • Make an optimize call to get P 1 itself P 3, 100 q 3 Sel 1 Lower bound on optimal cost: depends only on instances in 3 rd quadrant No other neighboring instance can be utilized by PCM assumption 10/30/2021 IIT-B visit 22

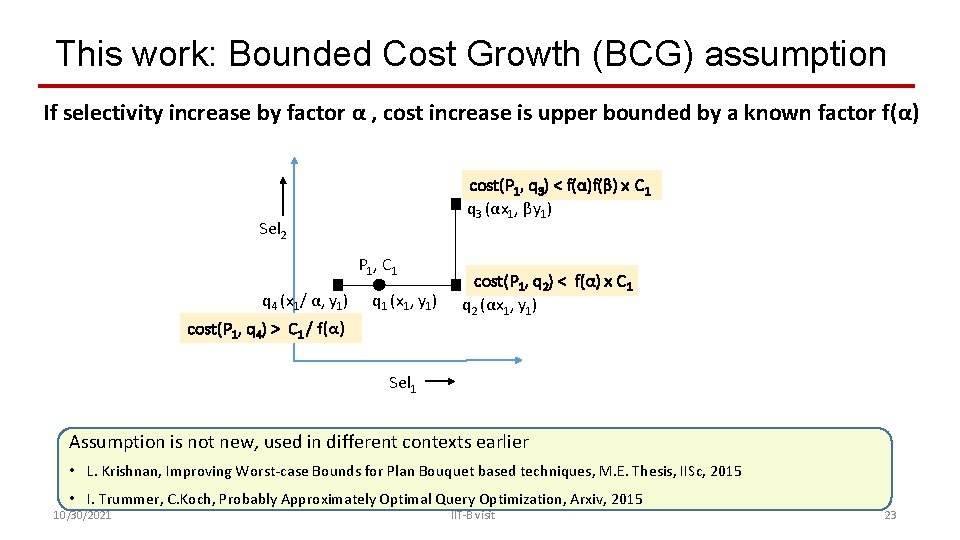
This work: Bounded Cost Growth (BCG) assumption If selectivity increase by factor α , cost increase is upper bounded by a known factor f(α) cost(P 1, q 3) < f(α)f(β) x C 1 q 3 (αx 1, βy 1) Sel 2 P 1, C 1 q 4 (x 1/ α, y 1) q 1 (x 1, y 1) cost(P 1, q 4) > C 1 / f(α) cost(P 1, q 2) < f(α) x C 1 q 2 (αx 1, y 1) Sel 1 Assumption is not new, used in different contexts earlier • L. Krishnan, Improving Worst-case Bounds for Plan Bouquet based techniques, M. E. Thesis, IISc, 2015 • I. Trummer, C. Koch, Probably Approximately Optimal Query Optimization, Arxiv, 2015 10/30/2021 IIT-B visit 23

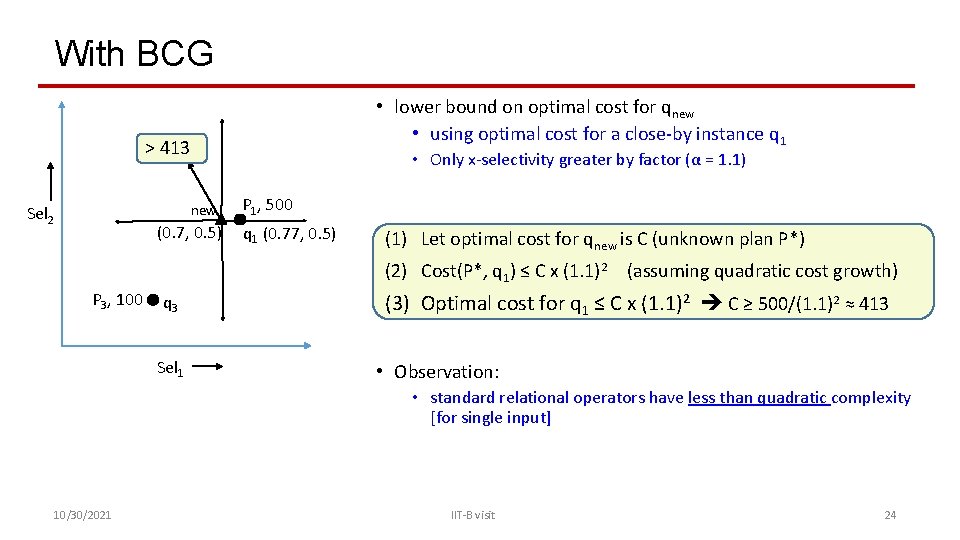
With BCG • lower bound on optimal cost for qnew • using optimal cost for a close-by instance q 1 > 413 • Only x-selectivity greater by factor (α = 1. 1) new Sel 2 (0. 7, 0. 5) P 1, 500 q 1 (0. 77, 0. 5) (1) Let optimal cost for qnew is C (unknown plan P*) (2) Cost(P*, q 1) ≤ C x (1. 1)2 (assuming quadratic cost growth) P 3, 100 q 3 Sel 1 (3) Optimal cost for q 1 ≤ C x (1. 1)2 C ≥ 500/(1. 1)2 ≈ 413 • Observation: • standard relational operators have less than quadratic complexity [for single input] 10/30/2021 IIT-B visit 24

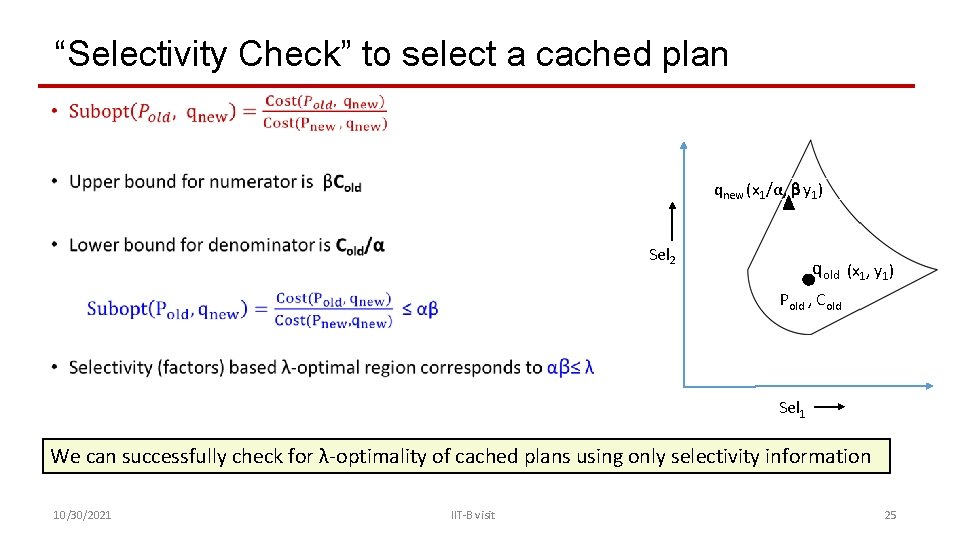
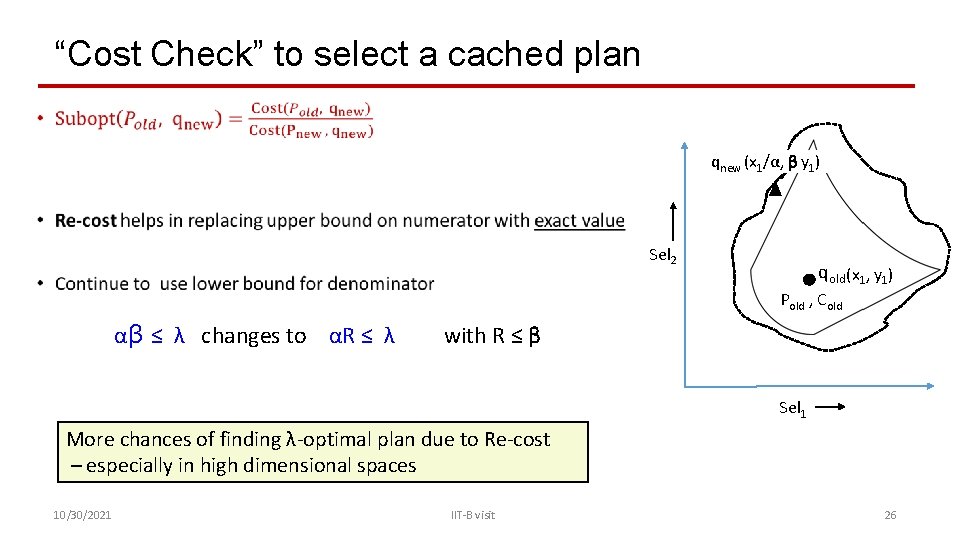
“Selectivity Check” to select a cached plan • qnew (x 1/α, β y 1) Sel 2 qold (x 1, y 1) Pold , Cold Sel 1 We can successfully check for λ-optimality of cached plans using only selectivity information 10/30/2021 IIT-B visit 25

“Cost Check” to select a cached plan • qnew (x 1/α, β y 1) Sel 2 qold (x 1, y 1) Pold , Cold αβ ≤ λ changes to αR ≤ λ with R ≤ β Sel 1 More chances of finding λ-optimal plan due to Re-cost – especially in high dimensional spaces 10/30/2021 IIT-B visit 26

Algorithm 1. do Selectivity check 2. if it fails to find a plan, do Cost check 3. if cost check fails, do optimize call For every new plan, do the Redundancy check 10/30/2021 IIT-B visit 27

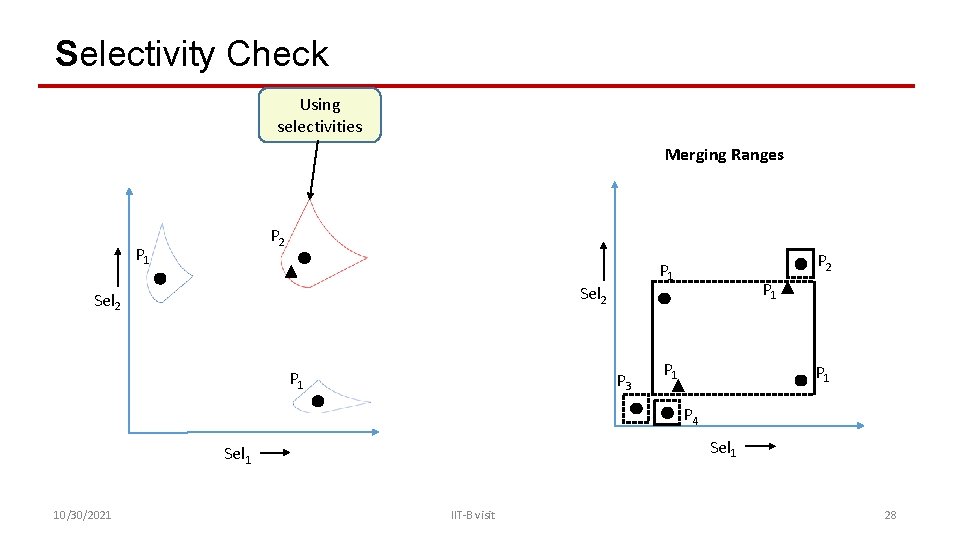
Selectivity Check Using selectivities Merging Ranges P 2 P 1 Sel 2 P 1 P 3 P 1 P 1 P 4 Sel 1 10/30/2021 IIT-B visit 28

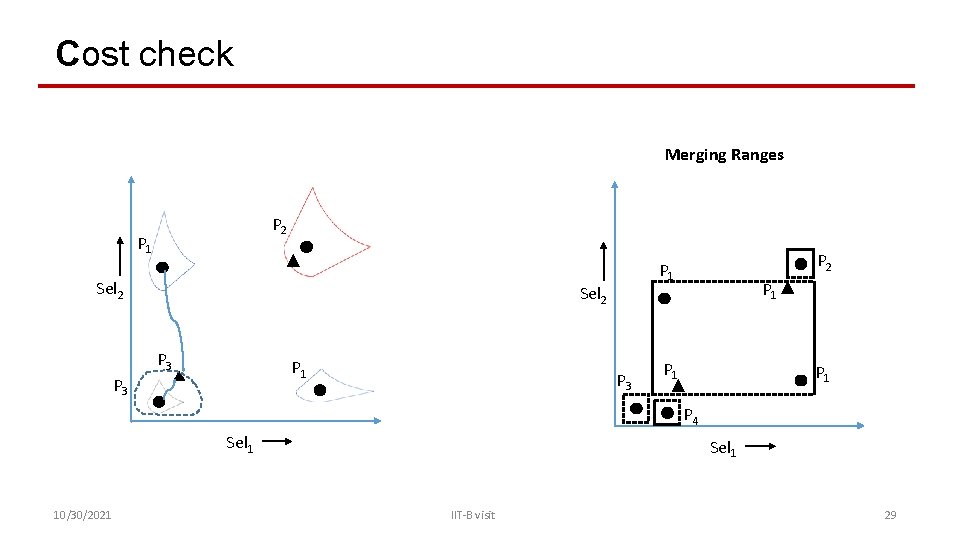
Cost check Merging Ranges P 2 P 1 Sel 2 P 3 P 1 P 3 P 2 P 1 P 3 P 1 P 1 P 4 Sel 1 10/30/2021 Sel 1 IIT-B visit 29

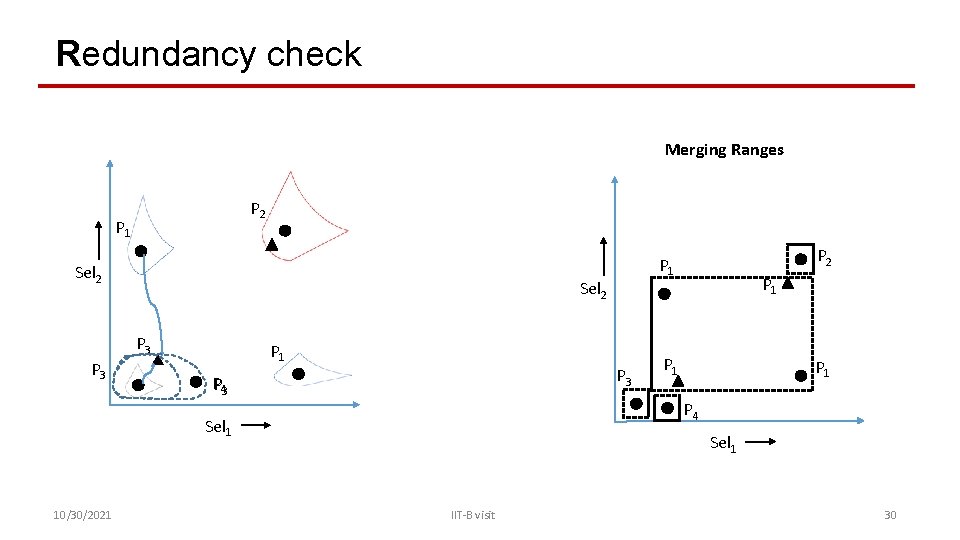
Redundancy check Merging Ranges P 2 P 1 Sel 2 P 3 P 1 P 3 P 43 P 1 P 1 P 4 Sel 1 10/30/2021 P 2 P 1 Sel 1 IIT-B visit 30

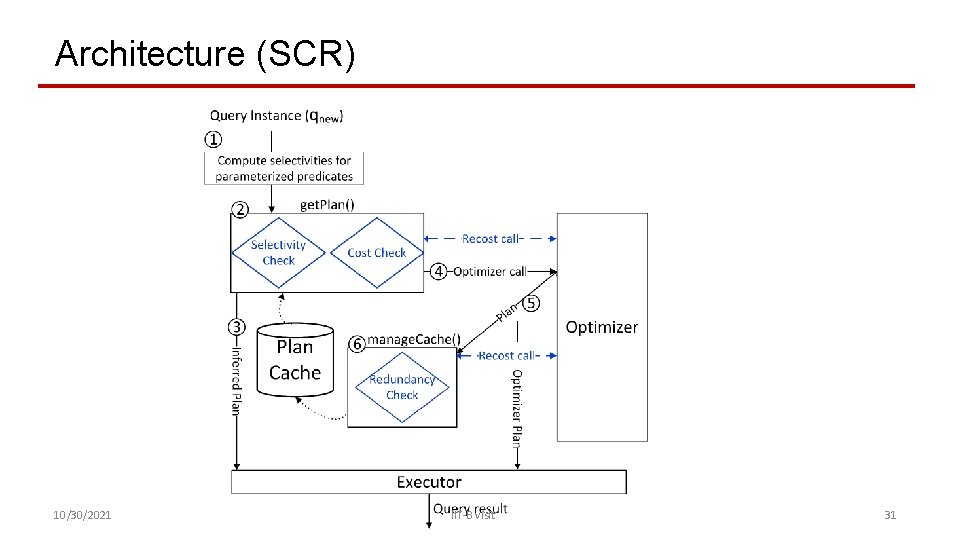
Architecture (SCR) 10/30/2021 IIT-B visit 31

Experimental Results 10/30/2021 IIT-B visit 32

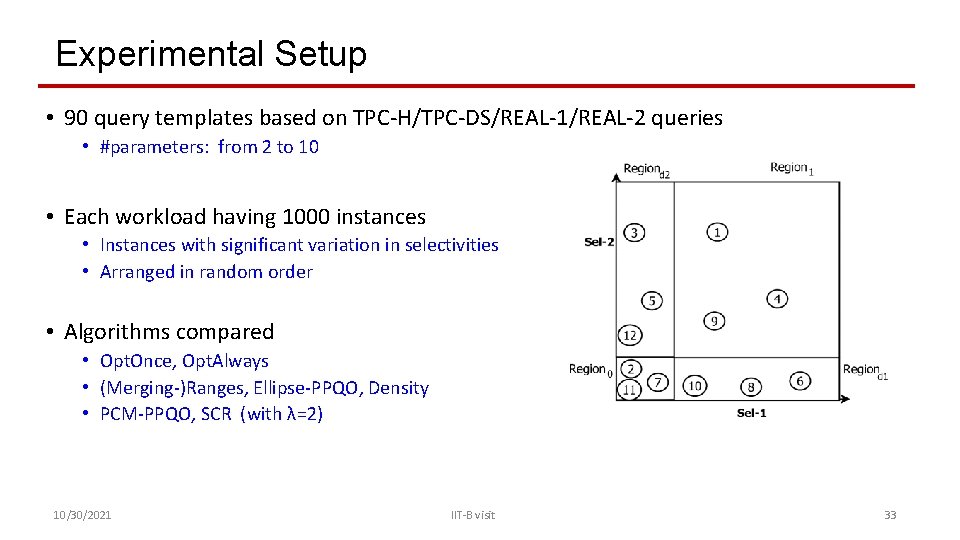
Experimental Setup • 90 query templates based on TPC-H/TPC-DS/REAL-1/REAL-2 queries • #parameters: from 2 to 10 • Each workload having 1000 instances • Instances with significant variation in selectivities • Arranged in random order • Algorithms compared • Opt. Once, Opt. Always • (Merging-)Ranges, Ellipse-PPQO, Density • PCM-PPQO, SCR (with λ=2) 10/30/2021 IIT-B visit 33

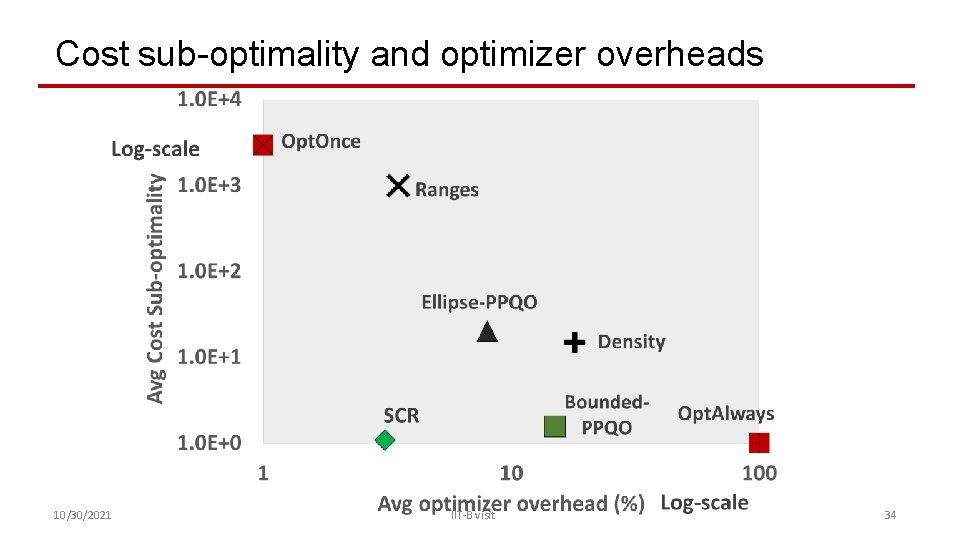
Cost sub-optimality and optimizer overheads 10/30/2021 IIT-B visit 34

Number of stored plans 50 Avg num. Plans 40 30 20 10/30/2021 PCM 2 SCR 2 Ellipse IIT-B visit Density Ranges 35

Summary • Proposed a new approach for optimization of parameterized queries • Matches/beats the performance of best techniques for different metrics • Optimizer calls ≈3% and Number of plans < 5 (average) 1. Use of Re-cost feature in online PQO • Selects best plan from cache • also helps in discarding redundant plans [small number of stored plans] 2. Bounded cost growth (BCG) assumption • Provide lower bound on optimal cost using any other query instance • Supports selectivity check • More efficient to ensure bounded sub-optimality 10/30/2021 IIT-B visit 36

Thanks! Questions?

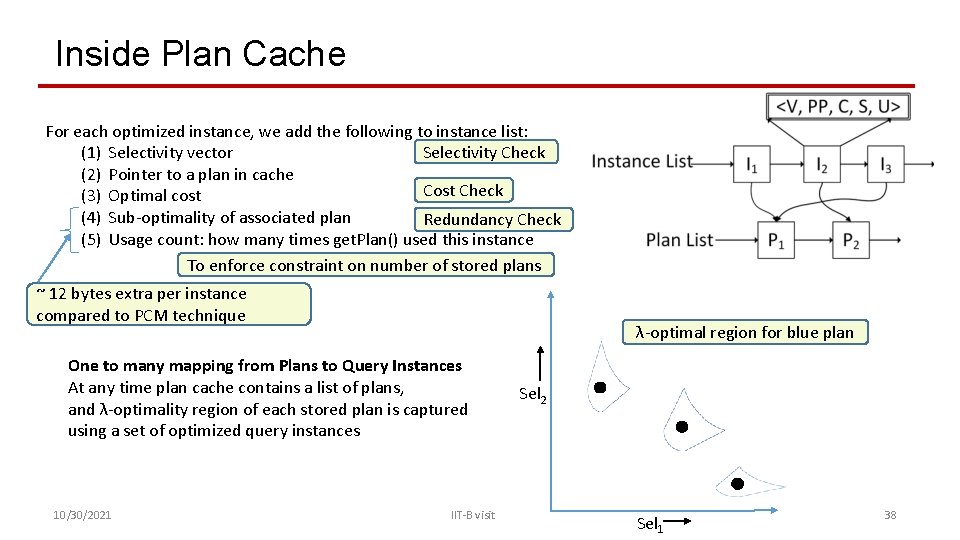
Inside Plan Cache For each optimized instance, we add the following to instance list: Selectivity Check (1) Selectivity vector (2) Pointer to a plan in cache Cost Check (3) Optimal cost (4) Sub-optimality of associated plan Redundancy Check (5) Usage count: how many times get. Plan() used this instance To enforce constraint on number of stored plans ~ 12 bytes extra per instance compared to PCM technique λ-optimal region for blue plan One to many mapping from Plans to Query Instances At any time plan cache contains a list of plans, and λ-optimality region of each stored plan is captured using a set of optimized query instances 10/30/2021 IIT-B visit Sel 2 Sel 1 38

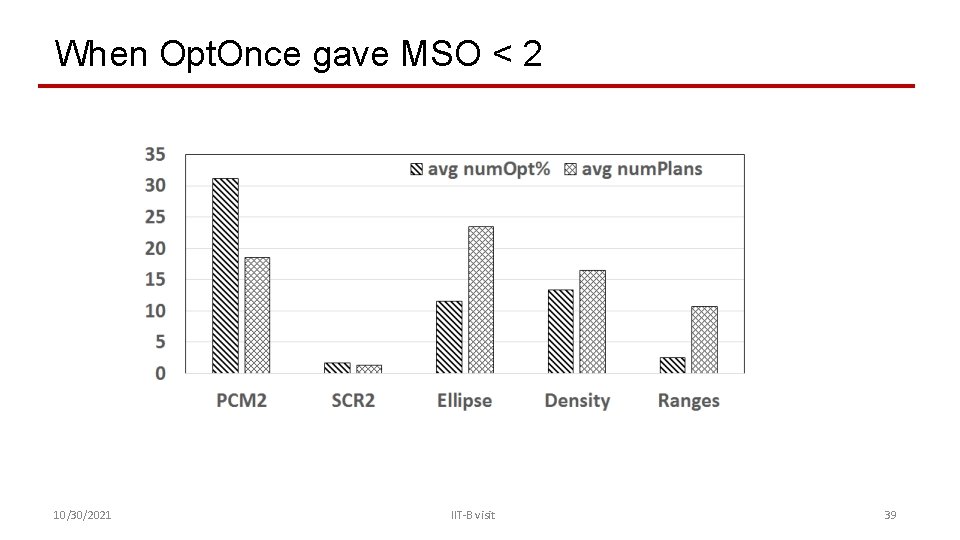
When Opt. Once gave MSO < 2 10/30/2021 IIT-B visit 39

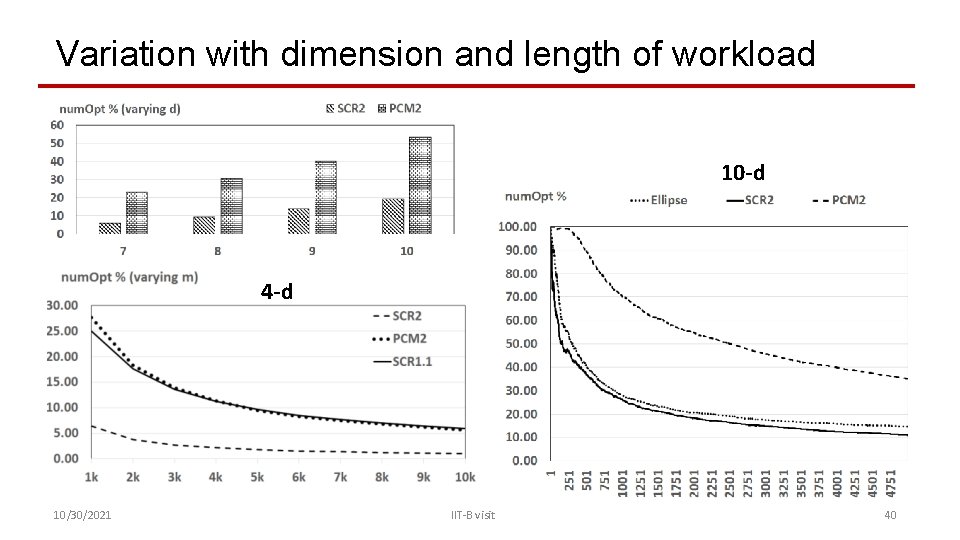
Variation with dimension and length of workload 10 -d 4 -d 10/30/2021 IIT-B visit 40

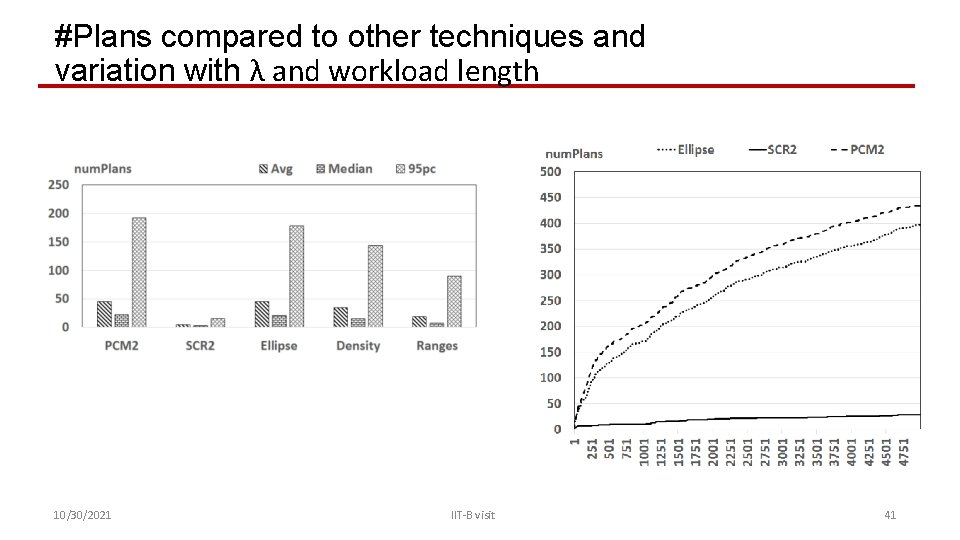
#Plans compared to other techniques and variation with λ and workload length 10/30/2021 IIT-B visit 41

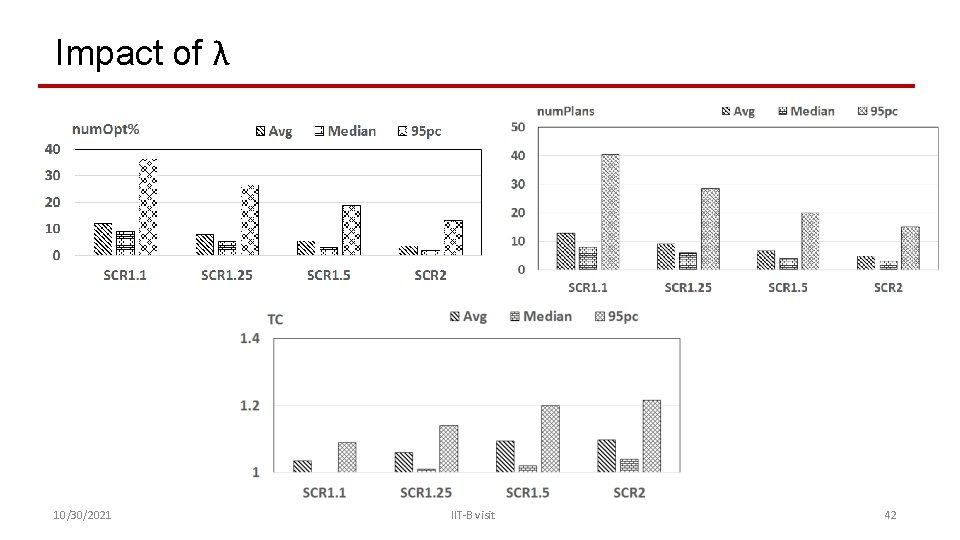
Impact of λ 10/30/2021 IIT-B visit 42