Levels of ProcessorMemory Hierarchy Can be Modeled by

Levels of Processor/Memory Hierarchy • Can be Modeled by Increasing Dimensionality of Data Array. – Additional dimension for each level of the hierarchy. – Envision data as reshaped to reflect increased dimensionality. – Calculus automatically transforms algorithm to reflect reshaped data array. – Data, layout, data movement, and scalarization automatically generated based on reshaped data array. University at Albany, SUNY lrm-1 lrm 12/25/2021

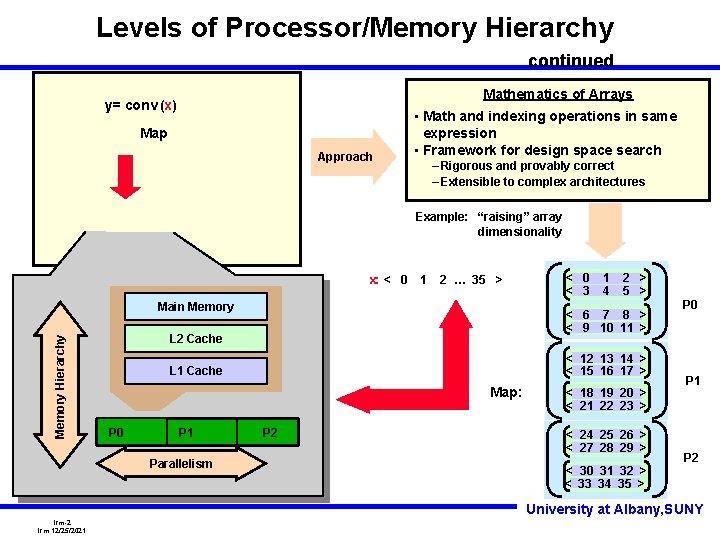
Levels of Processor/Memory Hierarchy continued Mathematics of Arrays y= conv (x) Map Approach • Math and indexing operations in same expression • Framework for design space search – Rigorous and provably correct – Extensible to complex architectures Example: “raising” array dimensionality x: < 0 1 2 … 35 > Memory Hierarchy Main Memory Map: Parallelism 2 > 5 > < 12 13 14 > < 15 16 17 > L 1 Cache P 1 1 4 < 6 7 8 > < 9 10 11 > L 2 Cache P 0 < 3 P 2 < 18 19 20 > < 21 22 23 > < 24 25 26 > < 27 28 29 > < 30 31 32 > < 33 34 35 > P 0 P 1 P 2 University at Albany, SUNY lrm-2 lrm 12/25/2021

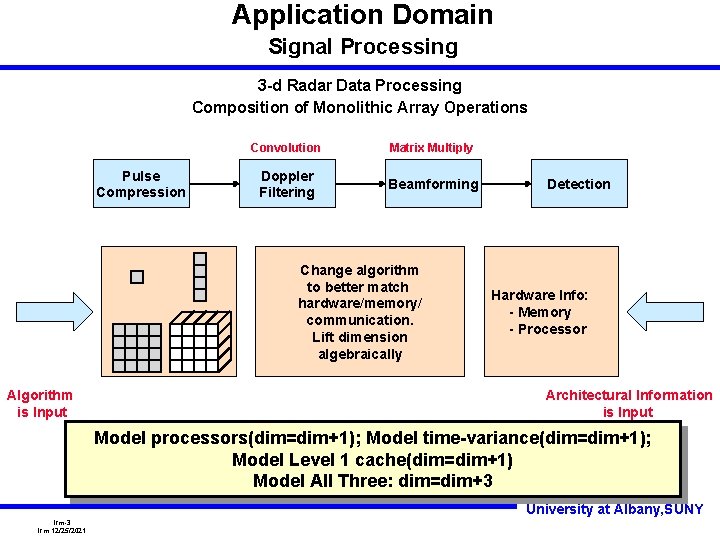
Application Domain Signal Processing 3 -d Radar Data Processing Composition of Monolithic Array Operations Pulse Compression Convolution Matrix Multiply Doppler Filtering Beamforming Change algorithm to better match hardware/memory/ communication. Lift dimension algebraically Algorithm is Input Detection Hardware Info: - Memory - Processor Architectural Information is Input Model processors(dim=dim+1); Model time-variance(dim=dim+1); Model Level 1 cache(dim=dim+1) Model All Three: dim=dim+3 University at Albany, SUNY lrm-3 lrm 12/25/2021

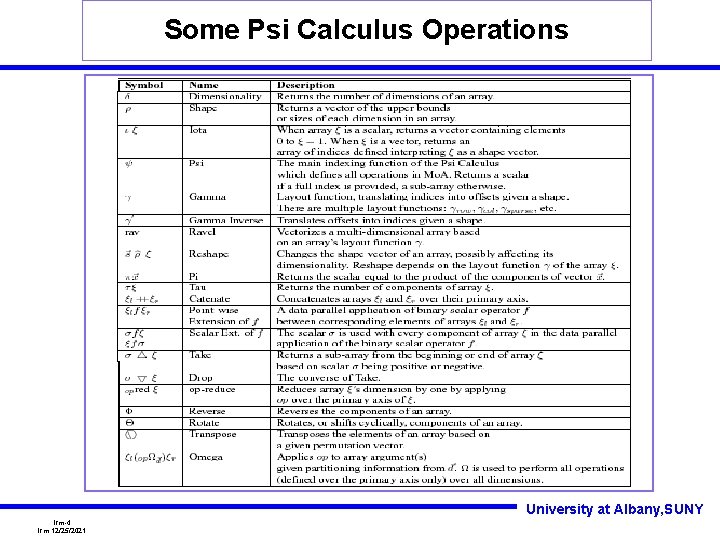
Some Psi Calculus Operations University at Albany, SUNY lrm-4 lrm 12/25/2021

Convolution: PSI Calculus Description Definition of y=conv(h, x) y[n]= where x ‘has N elements, h has M elements, 0≤n<N+M-1, and x’ is x padded by M-1 zeros on either end Psi Calculus Algorithm step Algorithm and PSI Calculus Description Initial step Form x’ rotate x’ (N+M-1) times take the size of h part of x’rot multiply sum x= < 1 2 3 4 > h= < 5 6 7 > x’=cat(reshape(<k-1>, <0>), cat(x, reshape(<k-1>, <0>)))= x’= < 0 0 1. . . 4 0 0 > x’ rot=binary. Omega(rotate, 0, iota(N+M-1), 1 x’) <0012. . . > x’ rot= < 0 1 2 3. . . > <1234. . . > x’ final=binary. Omega(take, 0, reshape<N+M-1>, <M>, =1, x’ rot <001> x’ final= < 0 1 2 > <123> Prod=binary. Omega (*, 1, h, 1, x’ final) <0 0 7 > Prod= < 0 6 14 > < 5 12 21 > Y=unary. Omega (sum, 1, Prod) Y= < 7 20 38. . . > PSI Calculus operators compose to form higher level operations University at Albany, SUNY lrm-5 lrm 12/25/2021

Experimental Platform and Method Hardware • DY 4 CHAMP-AV Board • – Contains 4 MPC 7400’s and 1 MPC 8420 MPC 7400 (G 4) – – 450 MHz 32 KB L 1 data cache 2 MB L 2 cache 64 MB memory/processor Software • Vx. Works 5. 2 – • Real-time OS Method • Run many iterations, report average, minimum, maximum time – GCC 2. 95. 4 (non-official release) – – GCC 2. 95. 3 with patches for Vx. Works Optimization flags: -O 3 -funroll-loops -fstrict-aliasing • • • From 10, 000 iterations for small data sizes, to 1000 for large data sizes All approaches run on same data Only average times shown here Only one G 4 processor used • Use of the Vx. Works OS resulted in very low variability in timing • High degree of confidence in results University at Albany, SUNY lrm-6 lrm 12/25/2021

Convolution and Dimension Lifting • Model Processor and Level 1 cache. – Start with 1 -d inputs(input dimension). – Envision 2 nd dimension ranging over output values. – Envision Processors Reshaped into a 3 rd dimension. The 2 nd dimension is partitioned. – Envision Cache Reshaped into a 4 th dimension. The 1 st dimension is partitioned. – “psi” Reduce to Normal Form University at Albany, SUNY lrm-7 lrm 12/25/2021

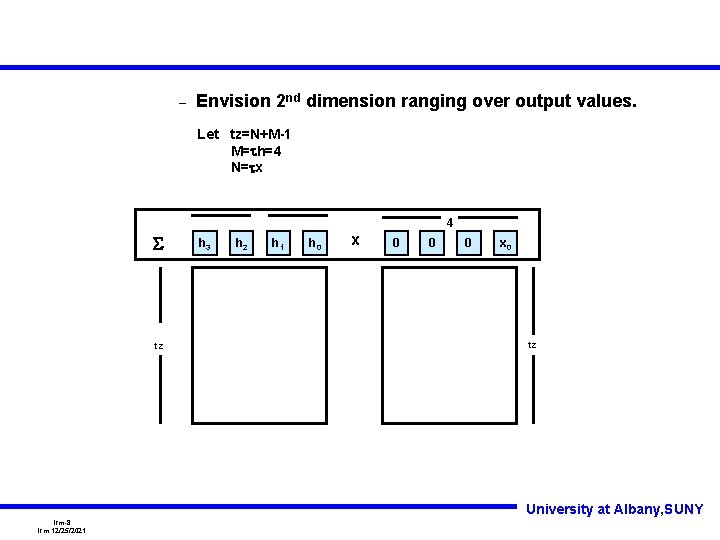
– Envision 2 nd dimension ranging over output values. Let tz=N+M-1 M=th=4 N=tx 4 S tz h 3 h 2 h 1 h 0 x 0 0 0 x 0 tz University at Albany, SUNY lrm-8 lrm 12/25/2021

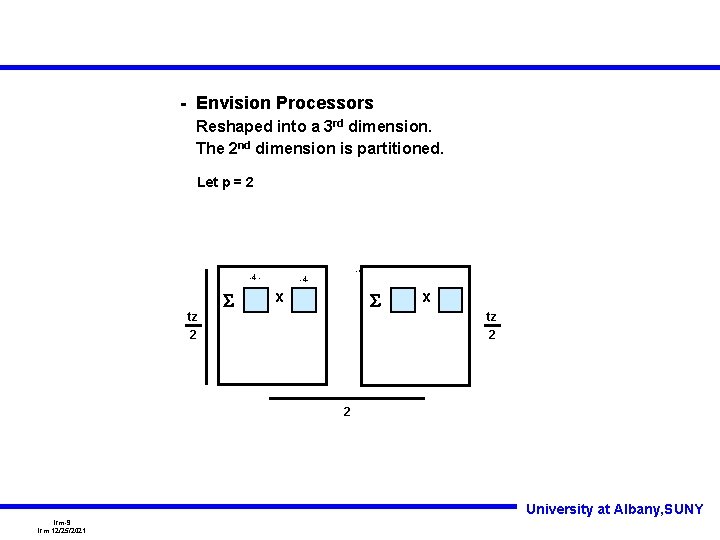
- Envision Processors Reshaped into a 3 rd dimension. The 2 nd dimension is partitioned. Let p = 2 -4 - tz 2 S -4 -4 - x S x tz 2 2 University at Albany, SUNY lrm-9 lrm 12/25/2021

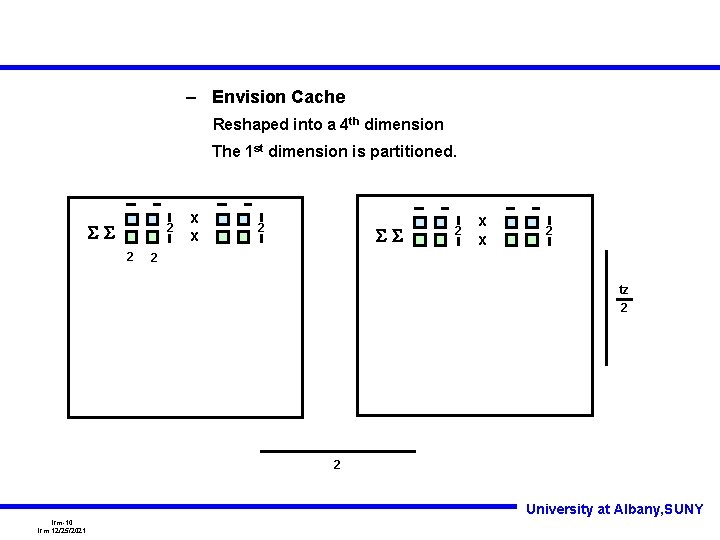
– Envision Cache Reshaped into a 4 th dimension The 1 st dimension is partitioned. SS 2 2 x x 2 SS 2 x x 2 2 tz/2 Tz/2 tz 2 Tz/2 2 University at Albany, SUNY lrm-10 lrm 12/25/2021

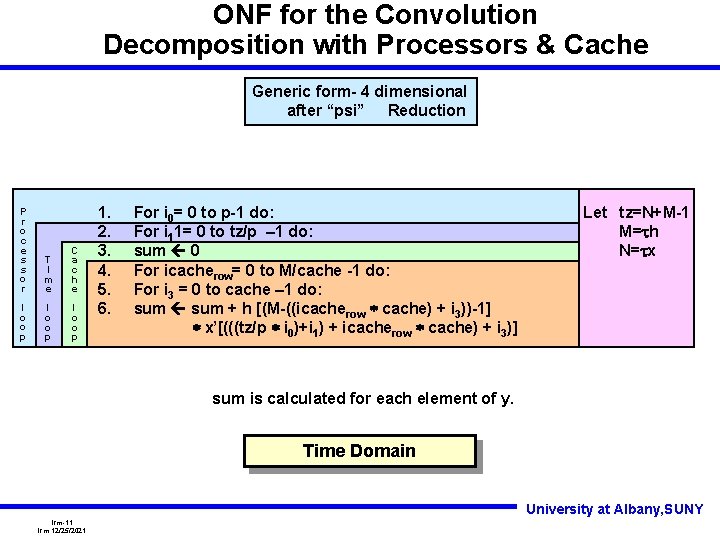
ONF for the Convolution Decomposition with Processors & Cache Generic form- 4 dimensional after “psi” Reduction P r o c e s s o r T I m e C a c h e l o o p 1. 2. 3. 4. 5. 6. For i 0= 0 to p-1 do: For i 11= 0 to tz/p – 1 do: sum 0 For icacherow= 0 to M/cache -1 do: For i 3 = 0 to cache – 1 do: sum + h [(M-((icacherow * cache) + i 3))-1] * x’[(((tz/p * i 0)+i 1) + icacherow * cache) + i 3)] Let tz=N+M-1 M=th N=tx sum is calculated for each element of y. Time Domain University at Albany, SUNY lrm-11 lrm 12/25/2021

Outline • • Overview Array Algebra: Mo. A and Index Calculus: Psi Calculus Time Domain Convolution Other algorithms in Radar – Modified Gram-Schmidt QR Decompositions MOA to ONF Experiments – Composition of Matrix Multiplication in Beamforming Mo. A to DNF Experiments – FFT • Benefits of Using Moa and Psi Calculus University at Albany, SUNY lrm-12 lrm 12/25/2021

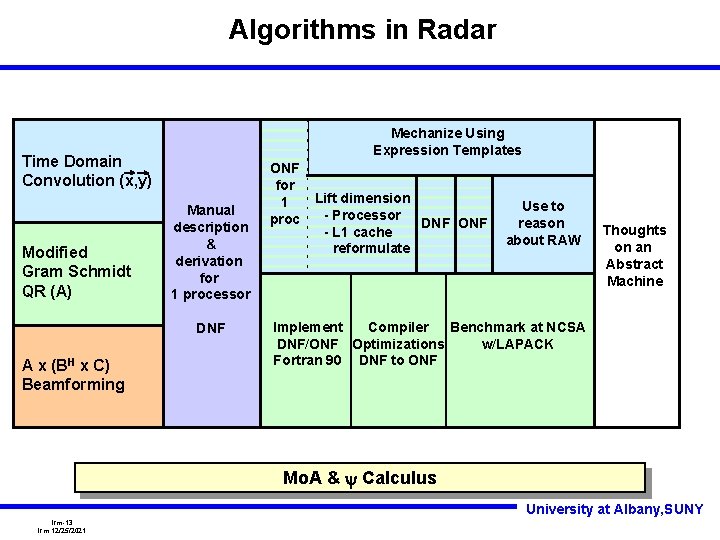
Algorithms in Radar Mechanize Using Expression Templates Time Domain Convolution (x, y) Modified Gram Schmidt QR (A) Manual description & derivation for 1 processor DNF A x (BH x C) Beamforming ONF for 1 proc Lift dimension - Processor DNF ONF - L 1 cache reformulate Use to reason about RAW Thoughts on an Abstract Machine Implement Compiler Benchmark at NCSA DNF/ONF Optimizations w/LAPACK Fortran 90 DNF to ONF Mo. A & y Calculus University at Albany, SUNY lrm-13 lrm 12/25/2021

Benefits of Using Moa and Psi Calculus • • • Processor/Memory Hierarchy can be modeled by reshaping data using an extra dimension for each level. Composition of monolithic operations can be reexpressed as composition of operations on smaller data granularities – Matches memory hierarchy levels – Avoids materialization of intermediate arrays. Algorithm can be automatically(algebraically) transformed to reflect array reshapings above. Facilitates programming expressed at a high level – Facilitates intentional program design and analysis – Facilitates portability This approach is applicable to many other problems in radar. University at Albany, SUNY lrm-14 lrm 12/25/2021

ONF for the QR Decomposition with Processors & Cache Initialization M a i n L o o p Processor Loop Compute Norm Processor Loop Normalize Processor Cache Loop Do. T Product Processor Cache Loop Ortothogonalize Modified Gram Schmidt University at Albany, SUNY lrm-15 lrm 12/25/2021

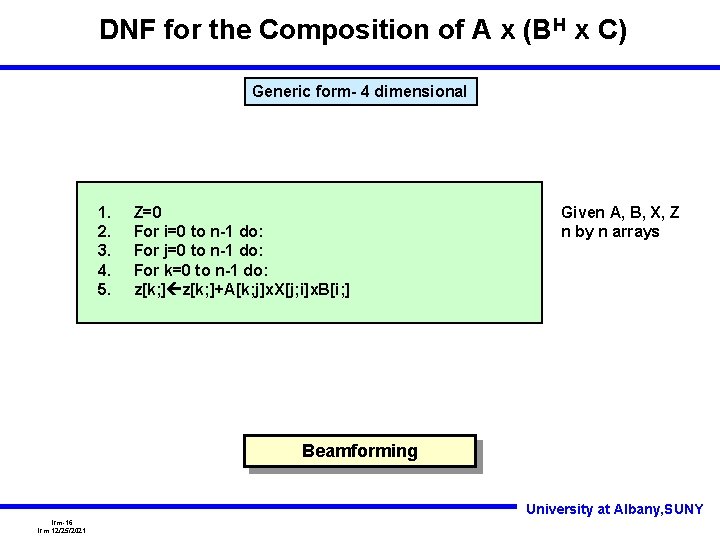
DNF for the Composition of A x (BH x C) Generic form- 4 dimensional 1. 2. 3. 4. 5. Z=0 For i=0 to n-1 do: For j=0 to n-1 do: For k=0 to n-1 do: z[k; ]+A[k; j]x. X[j; i]x. B[i; ] Given A, B, X, Z n by n arrays Beamforming University at Albany, SUNY lrm-16 lrm 12/25/2021

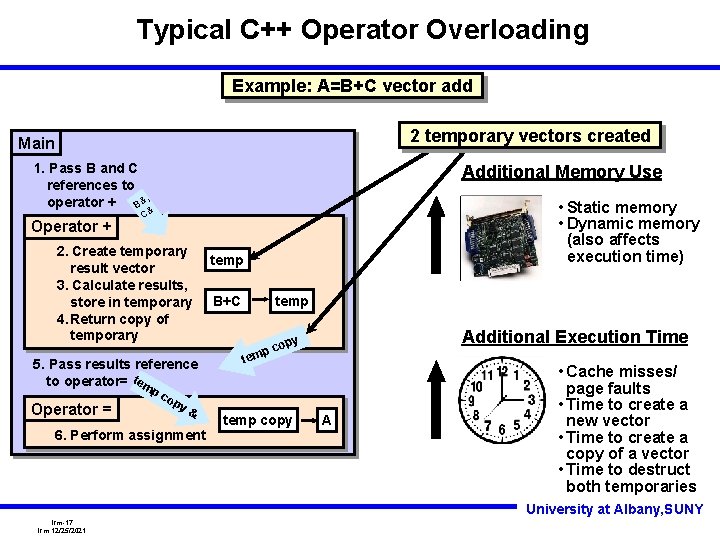
Typical C++ Operator Overloading Example: A=B+C vector add 2 temporary vectors created Main 1. Pass B and C references to operator + B&, Operator + Additional Memory Use 2. Create temporary result vector 3. Calculate results, store in temporary 4. Return copy of temporary 5. Pass results reference to operator= tem Operator = • Static memory • Dynamic memory (also affects execution time) C& pc temp B+C temp Additional Execution Time opy pc tem op y& 6. Perform assignment temp copy A • Cache misses/ page faults • Time to create a new vector • Time to create a copy of a vector • Time to destruct both temporaries University at Albany, SUNY lrm-17 lrm 12/25/2021

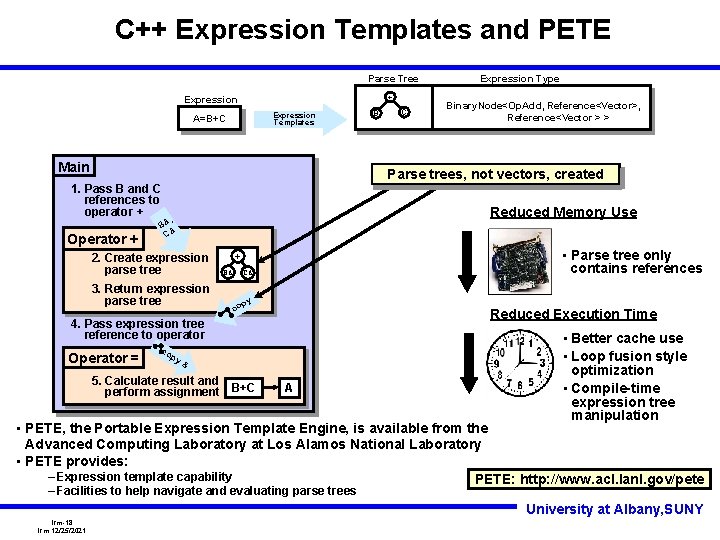
C++ Expression Templates and PETE Parse Tree + Expression Templates A=B+C Main Binary. Node<Op. Add, Reference<Vector>, Reference<Vector > > Reduced Memory Use , B& & C 2. Create expression parse tree 3. Return expression parse tree • Parse tree only contains references + B& C& py co Reduced Execution Time 4. Pass expression tree reference to operator Operator = C Parse trees, not vectors, created 1. Pass B and C references to operator + Operator + B Expression Type co py & 5. Calculate result and perform assignment B+C A • Better cache use • Loop fusion style optimization • Compile-time expression tree manipulation • PETE, the Portable Expression Template Engine, is available from the Advanced Computing Laboratory at Los Alamos National Laboratory • PETE provides: – Expression template capability PETE: http: //www. acl. lanl. gov/pete – Facilities to help navigate and evaluating parse trees University at Albany, SUNY lrm-18 lrm 12/25/2021

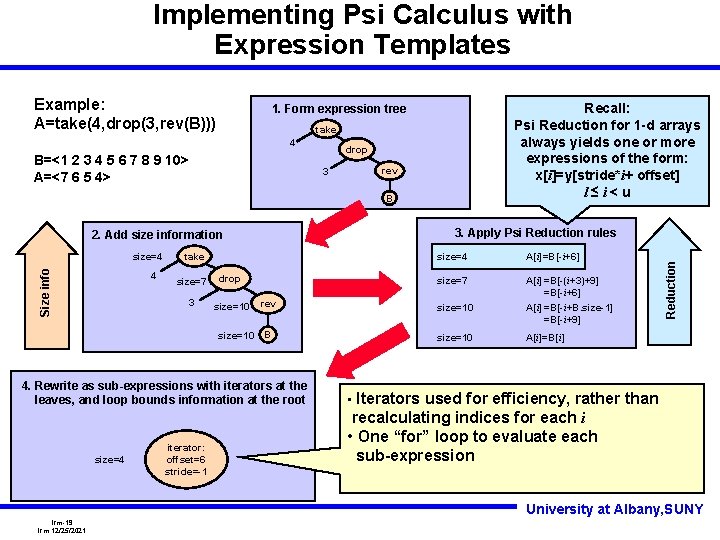
Implementing Psi Calculus with Expression Templates Recall: Psi Reduction for 1 -d arrays always yields one or more expressions of the form: x[i]=y[stride*i+ offset] l≤i<u 1. Form expression tree take 4 B=<1 2 3 4 5 6 7 8 9 10> A=<7 6 5 4> drop 3 rev B 3. Apply Psi Reduction rules 2. Add size information Size info size=4 4 take size=7 drop 3 size=10 iterator: offset=6 stride=-1 A[i]=B[-i+6] size=7 A[i] =B[-(i+3)+9] =B[-i+6] A[i] =B[-i+B. size-1] =B[-i+9] rev size=10 B size=10 4. Rewrite as sub-expressions with iterators at the leaves, and loop bounds information at the root size=4 Reduction Example: A=take(4, drop(3, rev(B))) A[i]=B[i] • Iterators used for efficiency, rather than recalculating indices for each i • One “for” loop to evaluate each sub-expression University at Albany, SUNY lrm-19 lrm 12/25/2021