Level 2 Certificate Further Mathematics 8360 Route Map

Level 2 Certificate Further Mathematics 8360 Route Map The following route map shows how the Level 2 Certificate in Further Mathematics topics can be taught over a one year period. The topic titles are those used in the Assessment Guidance and also on the All About Maths Site. Each tile is linked to a topic page so it is possible to see quickly the scope of assessment for the topic. Topic Level 2 Certificate in Further Mathematics 8360

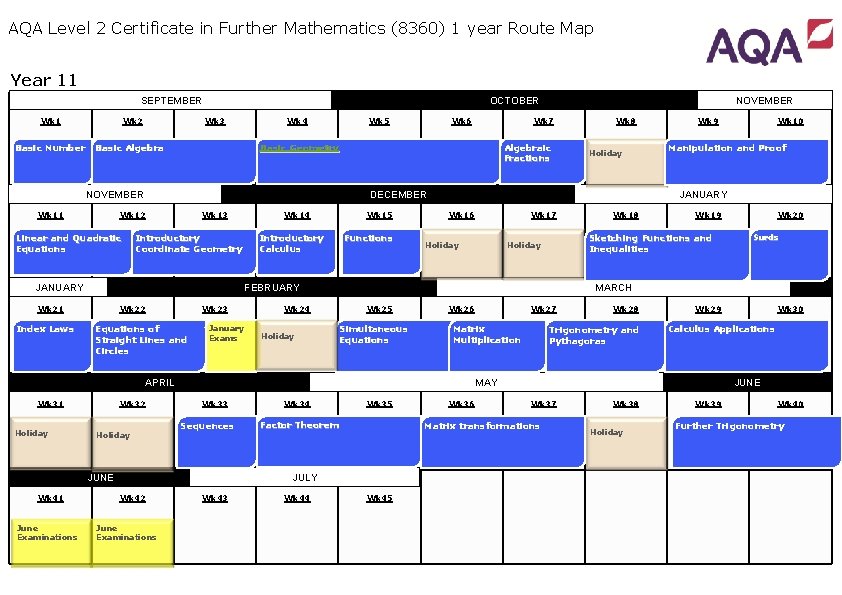
AQA Level 2 Certificate in Further Mathematics (8360) 1 year Route Map Year 11 OCTOBER SEPTEMBER Wk 1 Basic Number Wk 2 Wk 3 Basic Algebra Wk 4 Wk 5 Algebraic Fractions Wk 13 Introductory Coordinate Geometry JANUARY Index Laws Wk 22 Wk 23 Equations of Straight Lines and Circles Wk 14 Wk 15 Introductory Calculus Functions Wk 16 Holiday January Exams Wk 32 Holiday Wk 25 Simultaneous Equations Wk 33 Sequences June Examinations Wk 34 Wk 35 Factor Theorem June Examinations Wk 19 Sketching Functions and Inequalities Holiday Wk 26 Wk 27 Matrix Multiplication Wk 28 Trigonometry and Pythagoras Wk 43 Wk 44 Wk 20 Surds Wk 29 Wk 36 Wk 45 Wk 30 Calculus Applications JUNE Wk 37 Matrix transformations JULY Wk 42 Wk 18 MARCH Wk 24 Holiday Wk 10 Manipulation and Proof MAY JUNE Wk 41 Wk 17 Holiday APRIL Wk 31 Holiday Wk 9 JANUARY FEBRUARY Wk 21 Wk 8 DECEMBER Wk 12 Linear and Quadratic Equations Wk 7 Basic Geometry NOVEMBER Wk 11 Wk 6 NOVEMBER Wk 38 Holiday Wk 39 Wk 40 Further Trigonometry

Basic Number Candidates should be able to: Ø understand use the correct hierarchy of operations Ø understand use ratio and proportion Ø understand use numbers in index form and standard form Ø understand rounding and give answers to an appropriate degree of accuracy Return to Routemap Teachers own notes

Basic Algebra Candidates should be able to: Ø understand use commutative, associative and distributive laws Ø understand use the hierarchy of operations Ø recall and apply knowledge of the basic processes of algebra, extending to more complex expressions, equations, formulae and identities Ø expand two or more brackets Ø simplify expressions by collecting like terms Ø factorise by taking out common factors from expressions Ø factorise expressions given in the form of a quadratic Ø factorise a difference of two squares Return to Routemap Teachers own notes

Basic Geometry Candidates should be able to: Ø understand perimeter Ø recall and use the formula for area of a rectangle Ø recall and use the formula × base × height for area of a triangle Ø use the formula absin. C for area of a triangle Ø recall and use formulae for circumference and area of a circle Ø recall and use formulae for volume of a cube, a cuboid, prisms and pyramids Ø use formulae for volume of a cone and of a sphere Ø understand use angle properties of parallel and intersecting lines Ø understand use angle properties of triangles and special types of quadrilaterals and polygons Ø understand use circle theorems Ø construct formal proofs using correct mathematical notation and vocabulary Ø understand use the formulae for sine rule and cosine rule Return to Routemap Teachers own notes

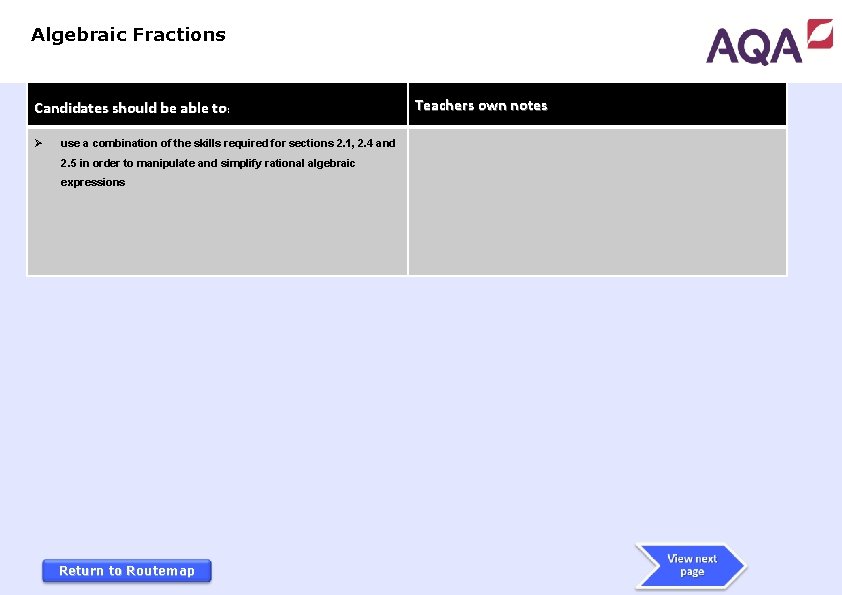
Algebraic Fractions Candidates should be able to: Ø use a combination of the skills required for sections 2. 1, 2. 4 and 2. 5 in order to manipulate and simplify rational algebraic expressions Return to Routemap Teachers own notes

Manipulation and Proof Candidates should be able to: Ø change the subject of a formula, where the subject appears on one or both sides of the formula Ø manipulate formulae and expressions Ø show one side of an identity can be manipulated to obtain the other side of the identity Ø show that an expression can be manipulated into another given form Ø prove given conditions for algebraic expressions Return to Routemap Teachers own notes

Linear and Quadratic Equations Candidates should be able to: Ø complete the square for any quadratic function of the form ax 2 + bx + c where a, b and c are integers Ø solve quadratic equations by completing the square Ø equate coefficients to obtain unknown values Ø solve linear equations Ø solve quadratic equations by factorisation, by graph, by completing the square or by formula Return to Routemap Teachers own notes

Introductory Coordinate Geometry Candidates should be able to: Ø work out the gradient of a line given two points on the line Ø select two points on a given line to work out the gradient Ø use the gradient of a line and a known point on the line to work out the co-ordinates of a different point on the line Ø work out the gradients of lines that are parallel and perpendicular to a given line Ø show that two lines are parallel or perpendicular using gradients Ø recall the formula or use a sketch diagram to obtain the appropriate lengths of sides Ø use the formula for the coordinates of the midpoint Ø use a given ratio to work out coordinates of a point given two other points Return to Routemap Teachers own notes

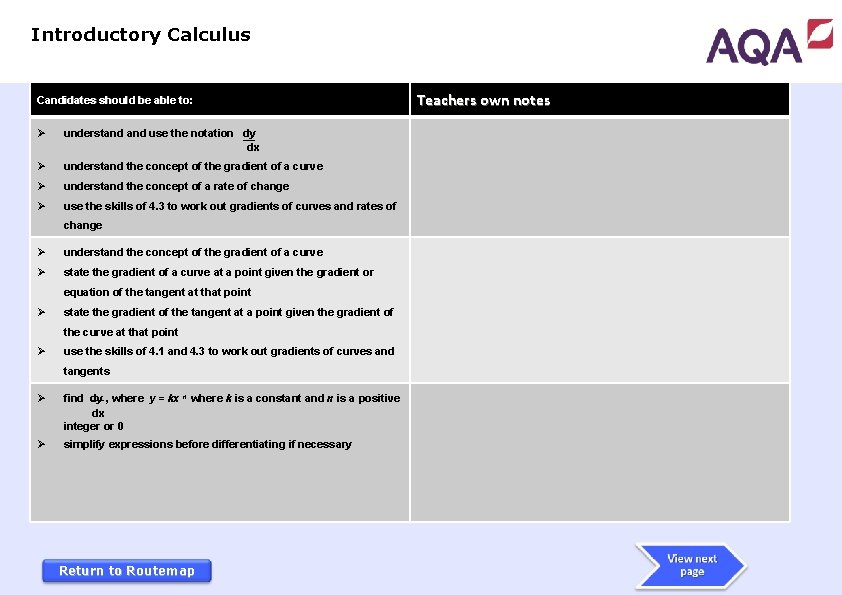
Introductory Calculus Candidates should be able to: Ø understand use the notation dy dx Ø understand the concept of the gradient of a curve Ø understand the concept of a rate of change Ø use the skills of 4. 3 to work out gradients of curves and rates of change Ø understand the concept of the gradient of a curve Ø state the gradient of a curve at a point given the gradient or equation of the tangent at that point Ø state the gradient of the tangent at a point given the gradient of the curve at that point Ø use the skills of 4. 1 and 4. 3 to work out gradients of curves and tangents Ø find dy , where y = kx n where k is a constant and n is a positive dx integer or 0 Ø simplify expressions before differentiating if necessary Return to Routemap Teachers own notes

Functions Candidates should be able to: Ø understand that a function is a relation between two sets of values Ø understand use function notation, for example f(x) Ø substitute values into a function, knowing that, for example f(2) is the value of the function when x = 2 Ø solve equations that use function notation Ø define the domain of a function Ø work out the range of a function Ø express a domain in a variety of forms, for example x > 2, for all x except x = 0, for all real values Ø express a range in a variety of forms, for example f(x) ≤ 0, for all f(x) except f(x) = 1 Return to Routemap Teachers own notes

Sketching Functions and Inequalities Candidates should be able to: Ø draw or sketch graphs of linear and quadratic functions with up to 3 domains Ø label points of intersection of graphs with the axes Ø understand that graphs should only be drawn within the given domain Ø identify any symmetries on a quadratic graph and from this determine the coordinates of the turning point Ø solve linear inequalities Ø solve quadratic inequalities Return to Routemap Teachers own notes

Surds Candidates should be able to: Ø simplify expressions by manipulating surds Ø expand brackets which contain surds Ø rationalise the denominator, including denominators in the form a √b + c √d where a, b, c and d are integers Ø understand the concept of using surds to give an exact answer Return to Routemap Teachers own notes

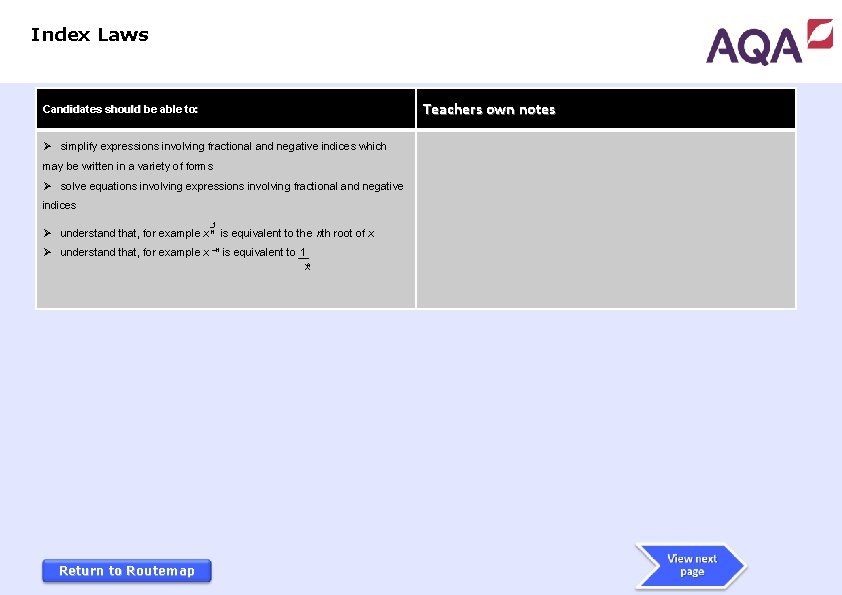
Index Laws Teachers own notes Candidates should be able to: Ø simplify expressions involving fractional and negative indices which may be written in a variety of forms Ø solve equations involving expressions involving fractional and negative indices 1 Ø understand that, for example x n is equivalent to the nth root of x Ø understand that, for example x n is equivalent to 1 xn Return to Routemap

Equations of Straight Lines and Circles Candidates should be able to: Ø work out the gradient and the intercepts with the axes of a given equation or graph Ø work out the equation of a line using the gradient and a known point on the line Ø work out the equation of a line using two known points on the line Ø give equations in a particular form when instructed to do so Ø work out coordinates of the point of intersection of two lines Ø draw a straight line using a given gradient and a given point on the line Ø draw a straight line using two given points on the line Return to Routemap (1 of 2) Teachers own notes

Equations of Straight Lines and Circles Candidates should be able to: (2 of 2) Teachers own notes Ø recognise the equation of a circle, centre (0, 0), radius r Ø write down the equation of a circle given centre (0, 0) and radius Ø work out coordinates of points of intersection of a given circle and a given straight line Ø recognise the equation of a circle, centre (a, b), radius r Ø write down the equation of a circle given centre (a, b) and radius Ø work out coordinates of points of intersection of a given circle and a given straight line Ø understand that the circle (x a) 2 + (y b) 2 = r 2 is a translation of the circle x 2 + y 2 = r 2 by the vector a b Return to Routemap Return to previous page

Simultaneous Equations Candidates should be able to: Ø solve two linear simultaneous equations using any valid method Ø solve simultaneous equations where one is linear and one is second order using substitution or any other valid method Return to Routemap Teachers own notes

Matrix Multiplication Candidates should be able to: Ø multiply a 2 × 2 matrix by a 2 × 1 matrix Ø multiply a 2 × 2 matrix by a 2 × 2 matrix Ø multiply 2 × 2 and 2 × 1 matrices by a scalar Ø understand that, in general, matrix multiplication is not commutative Ø understand that matrix multiplication is associative Ø understand that AI = IA = A Return to Routemap Teachers own notes

Trigonometry and Pythagoras Candidates should be able to: Ø work out any unknown side using two given sides Ø identify appropriate right-angled triangles in 2 and 3 dimensional shapes and apply Pythagoras’ theorem Ø recognise and use Pythagorean triples Ø identify appropriate right-angled triangles in 2 and 3 dimensional shapes and apply Pythagoras’ theorem Ø identify appropriate triangles in 2 and 3 dimensional shapes and apply trigonometry Ø work out the angle between a line and a plane Ø work out the angle between two planes Ø understand use bearings Ø recall or work out the exact values of the trigonometric ratios for angles 30 , 45 and 60 Return to Routemap Teachers own notes

Calculus Applications Candidates should be able to: Ø use the skills of 4. 2, 4. 3 and 3. 5 to work out the equation of a tangent to a curve Ø use the skills of 4. 2, 4. 3, 3. 2 and 3. 5 to work out the equation of a normal to a curve Ø understand that stationary points are points at which the gradient is zero Ø use the skills of 4. 3 to work out stationary points on a curve Ø Ø understand the meaning of increasing and decreasing functions Ø understand the meaning of maximum points, minimum points and points of inflection Ø prove whether a stationary point is a maximum, minimum or point of inflection Ø draw a sketch graph of a curve having used the skills of 4. 5 to work out the stationary points Return to Routemap Teachers own notes

Sequences Candidates should be able to: Ø write down the value of the nth term of a sequence for any given value of Ø work out a formula for the nth term of a sequence, which may contain linear or quadratic parts Ø work out the limiting value for a given sequence or for a given nth term as n approaches infinity Return to Routemap Teachers own notes

Factor Theorem Candidates should be able to: Ø understand use the factor theorem to factorise polynomials up to and including cubics Ø find integer roots of polynomial equations up to and including cubics Ø show that x a is a factor of the function f(x) by checking that f(a) =0 Ø solve equations up to and including cubics, where at least one of the roots is an integer Return to Routemap Teachers own notes

Matrix Transformations Candidates should be able to: Ø work out the image of any vertex of the unit square given the matrix operator Ø work out or recall the matrix operator for a given transformation Ø understand that the matrix product PQ represents the transformation with matrix Q followed by the transformation with matrix P Ø use the skills of 5. 1 to work out the matrix which represents a combined transformation Return to Routemap Teachers own notes

Further Trigonometry Candidates should be able to: Ø understand use the properties of the graphs of y = sin x, y = cos x and y = tan x for 0 x 360 Ø sketch and use the graphs to solve problems Ø recall the sign of sin , cos and tan for any positive angle up to 360 understand use the relationships between positive angles up to 360 (eg, sin(180 ) = sin ) Ø use the identities to simplify expressions Ø use the identities to prove other identities Ø use the identities in solution of equations Ø work out all solutions in a given interval Ø rearrange equations including the use of the identities from section 6. 9 Ø use factorisation Return to Routemap Teachers own notes