Lets Recapitulate 1 Regular Languages DFAs NFAs Regular




























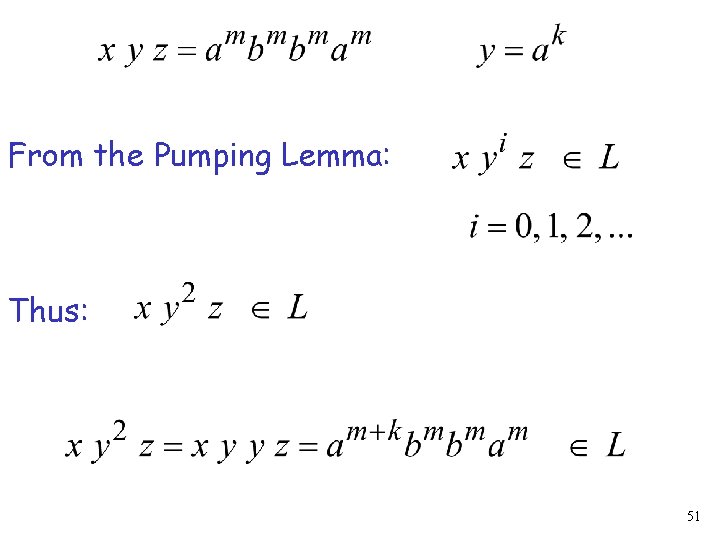


- Slides: 53
Let’s Recapitulate 1

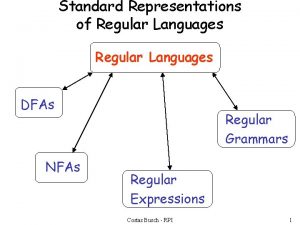
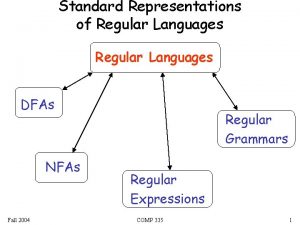
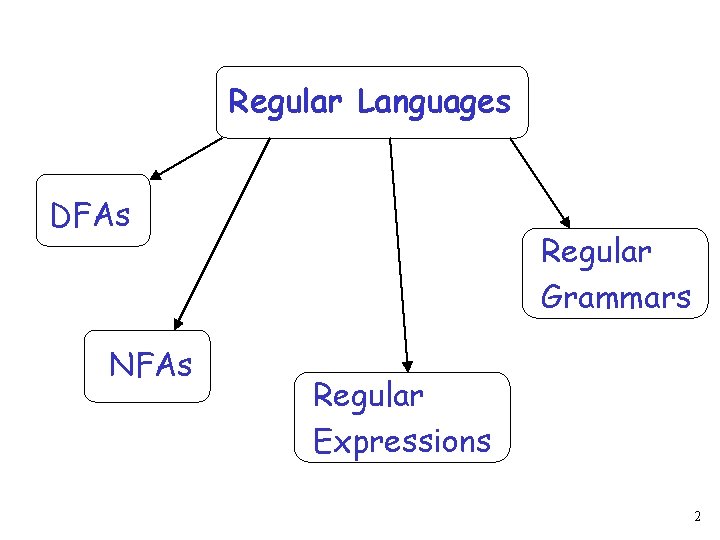
Regular Languages DFAs NFAs Regular Grammars Regular Expressions 2

A standard representation of a regular language : A DFA that accepts A NFA that accepts A regular expression that generates A regular grammar that generates 3

When we say: “We are given a Regular Language “ We mean: Language in a standard representation 4

Elementary Questions about Regular Languages 5

Question: Given regular language how can we check if a string ? 6

Question: Answer: Given regular language how can we check if a string ? Take the DFA that accepts and check if is accepted 7

Question: Answer: Given regular language how can we check if is empty, finite, infinite ? Take the DFA that accepts Then check the DFA 8

If there is a walk from the start state to a final state then: is not empty Otherwise empty If the walk contains a cycle then: is infinite Otherwise finite 9

Question: Given regular languages how can we check if and ? 10

Question: Given regular languages how can we check if and ? Answer: take And find if 11

Question: Given language how can we check if is not a regular language ? 12

Question: Given language how can we check if is not a regular language ? Answer: The answer is not obvious We need the Pumping Lemma 13

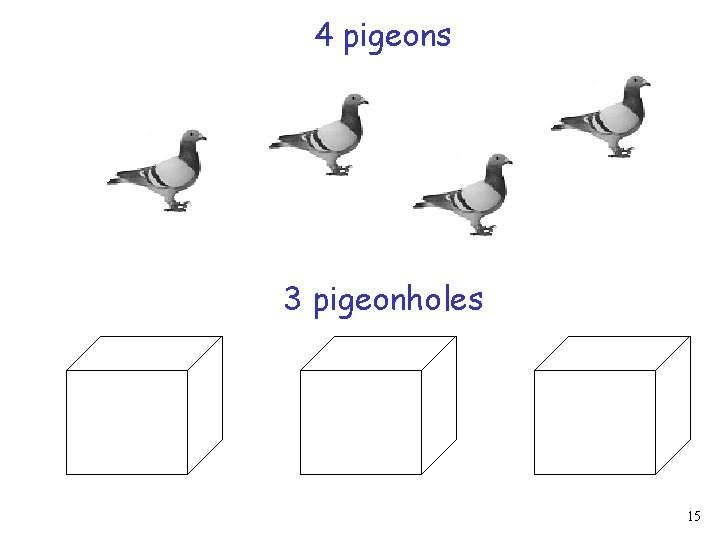
The Pigeonhole Principle 14

4 pigeons 3 pigeonholes 15

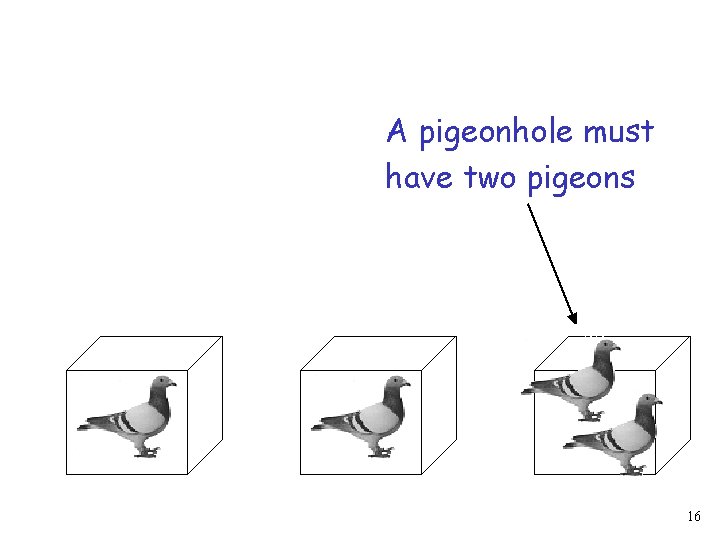
A pigeonhole must have two pigeons 16

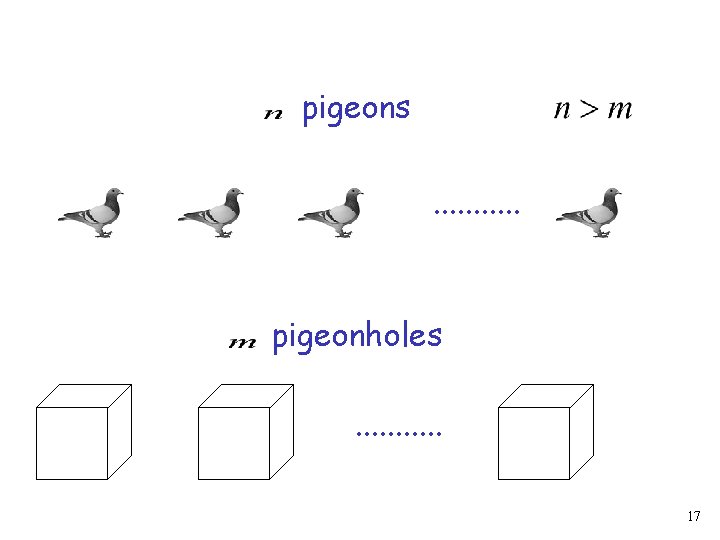
pigeons. . . pigeonholes. . . 17

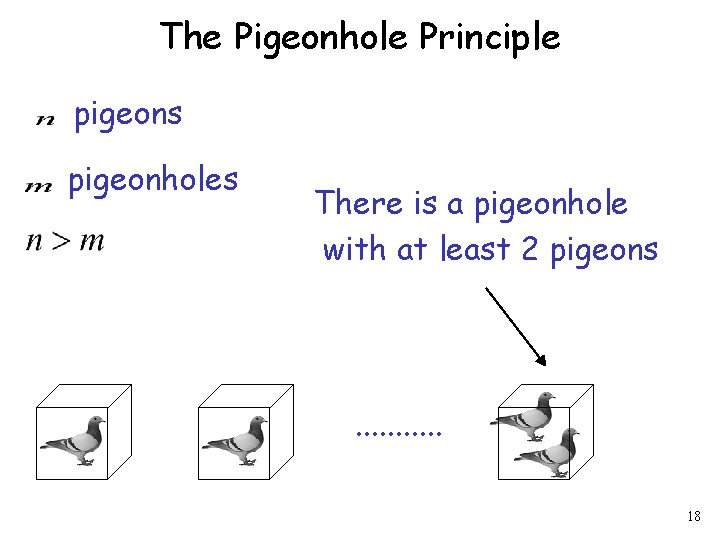
The Pigeonhole Principle pigeons pigeonholes There is a pigeonhole with at least 2 pigeons . . . 18

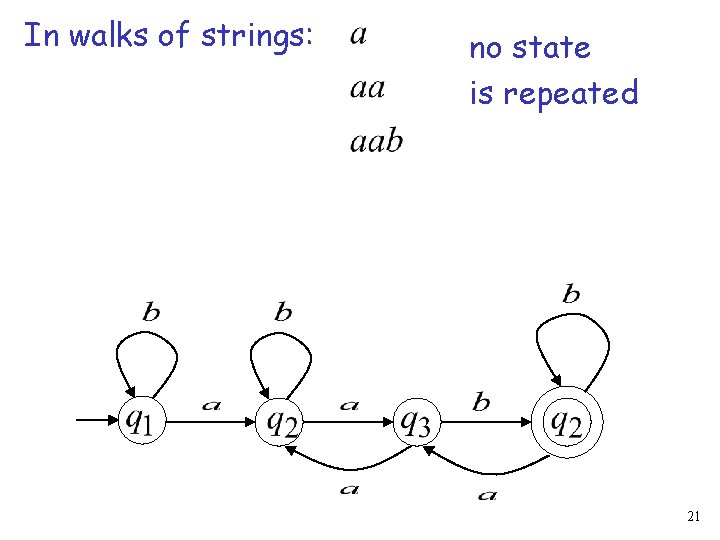
The Pigeonhole Principle and DFAs 19

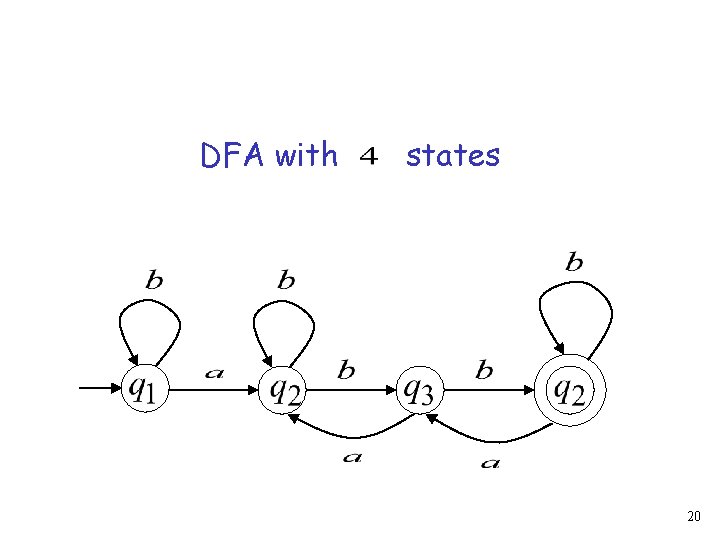
DFA with states 20

In walks of strings: no state is repeated 21

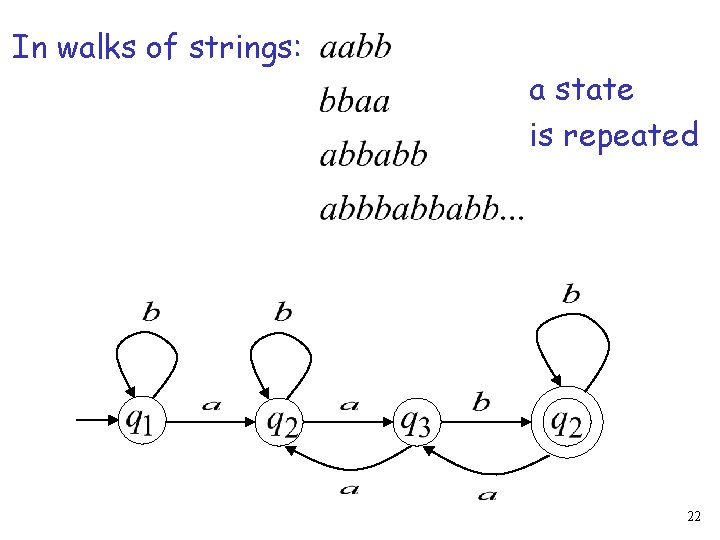
In walks of strings: a state is repeated 22

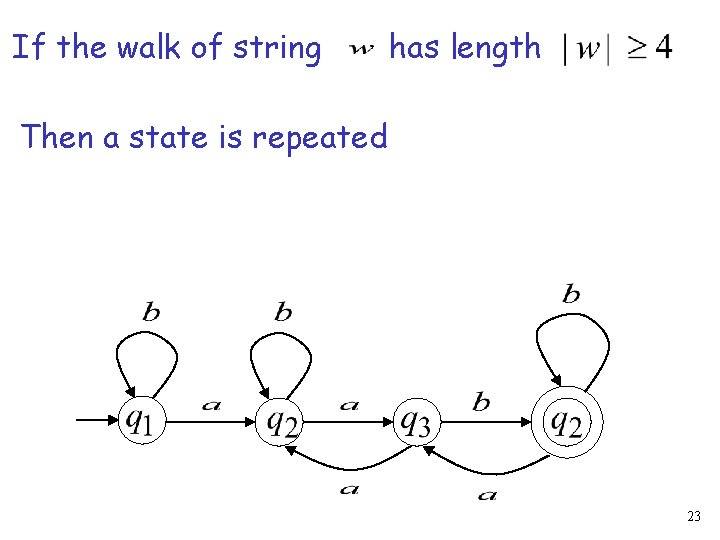
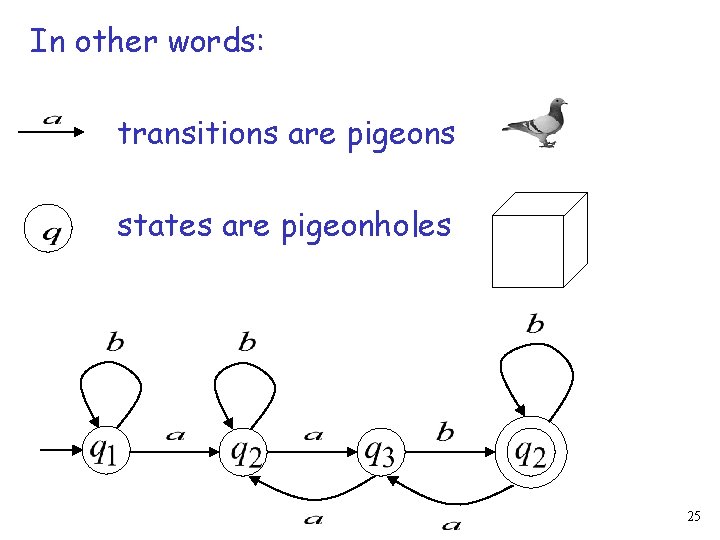
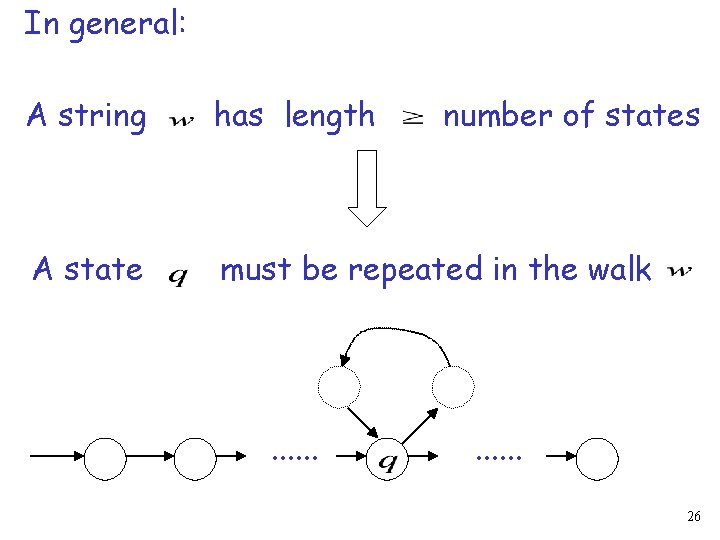
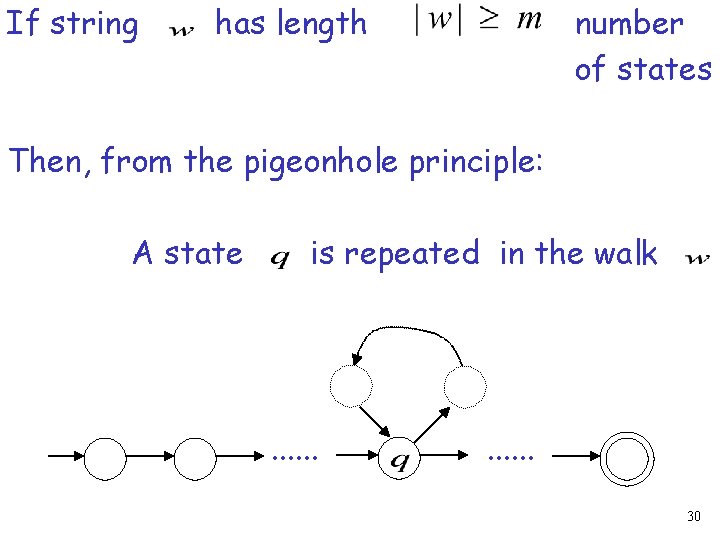
If the walk of string has length Then a state is repeated 23

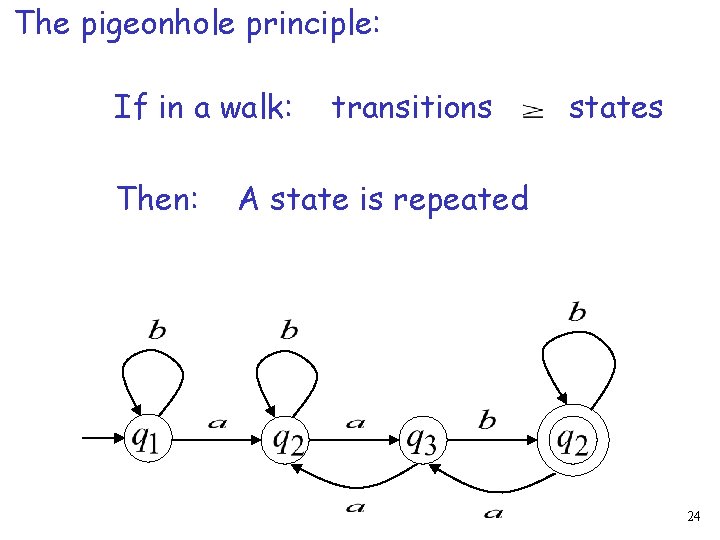
The pigeonhole principle: If in a walk: Then: transitions states A state is repeated 24

In other words: transitions are pigeons states are pigeonholes 25

In general: A string has length A state must be repeated in the walk . . . number of states . . . 26

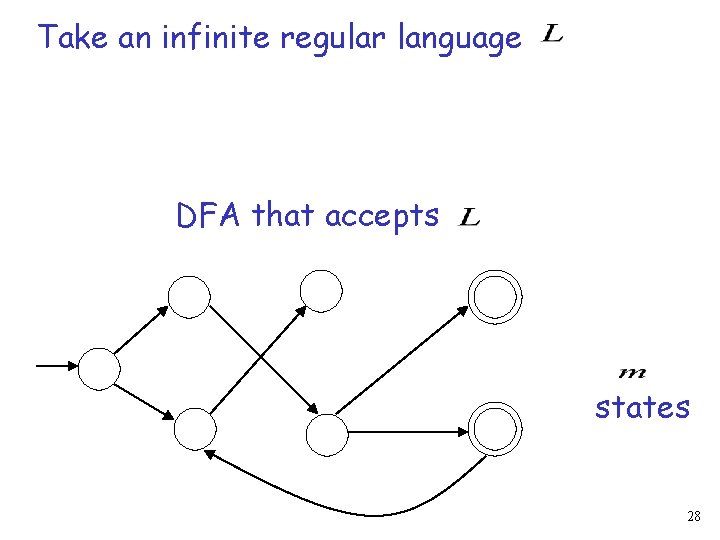
The Pumping Lemma 27

Take an infinite regular language DFA that accepts states 28

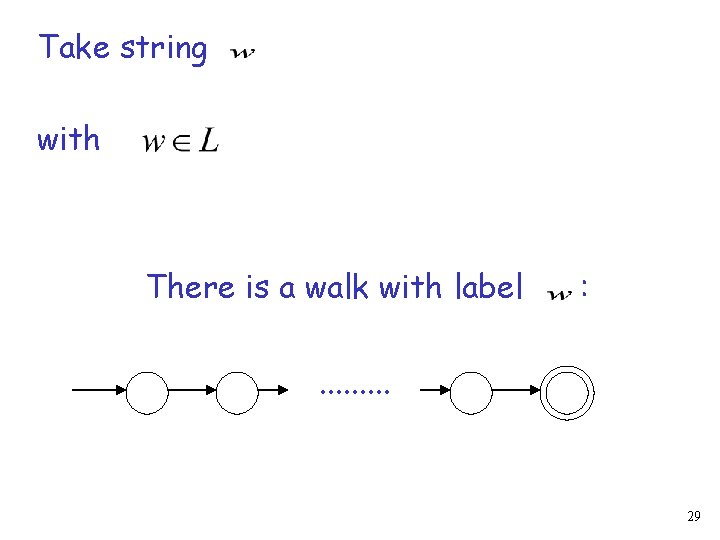
Take string with There is a walk with label : . . 29

If string number of states has length Then, from the pigeonhole principle: A state is repeated in the walk . . . 30

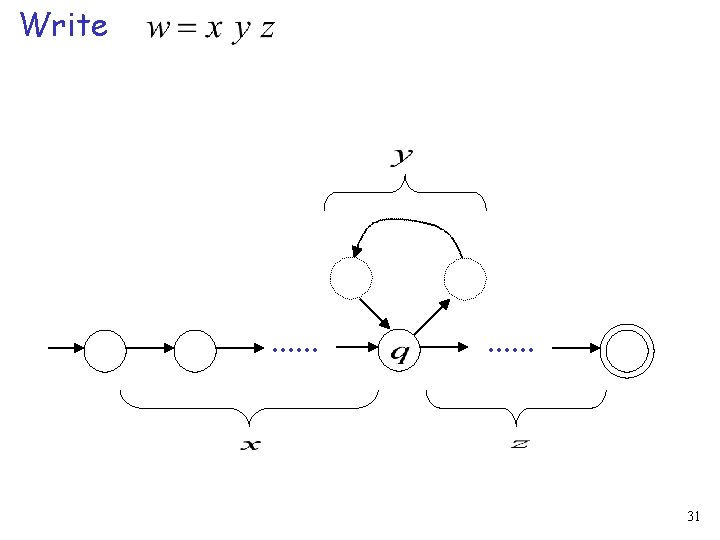
Write . . . 31

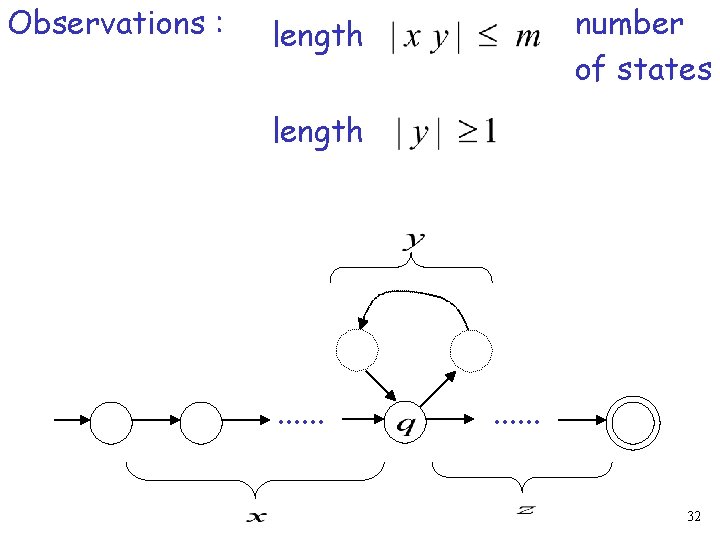
Observations : number of states length . . . 32

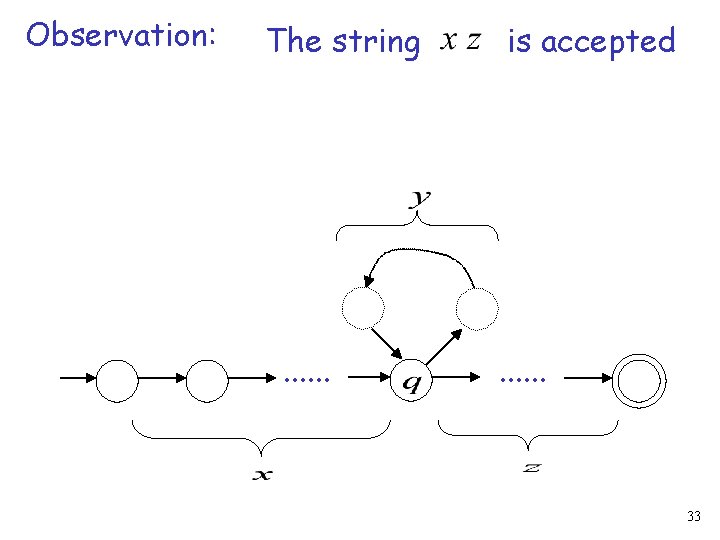
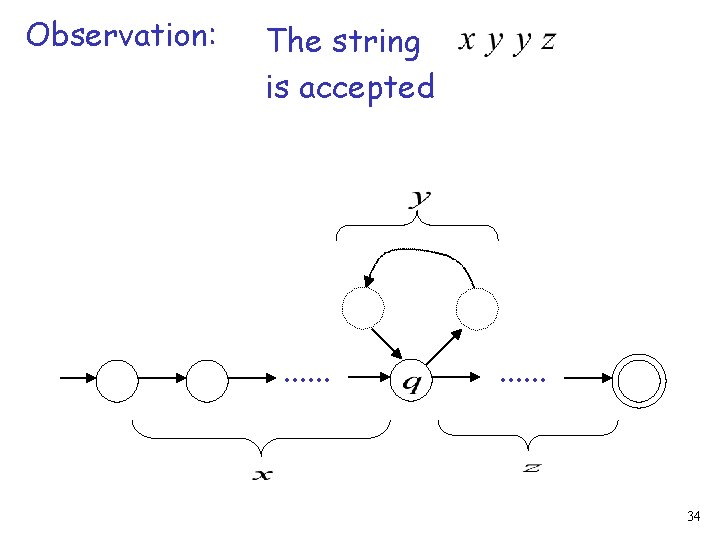
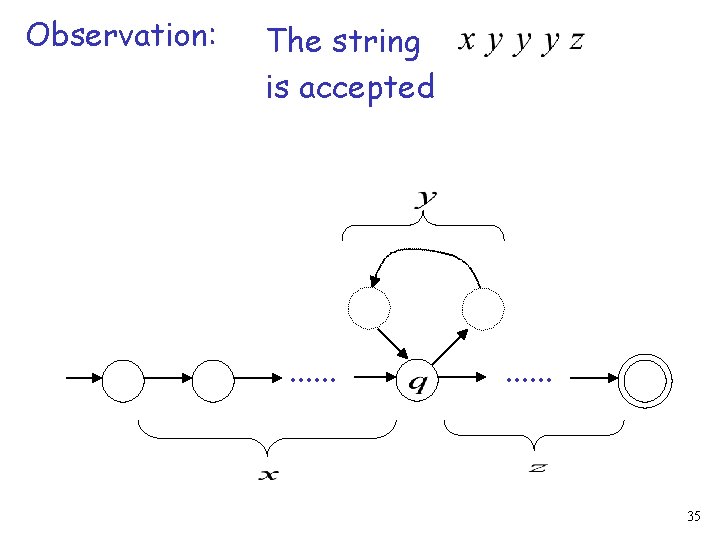
Observation: The string . . . is accepted . . . 33

Observation: The string is accepted . . . 34

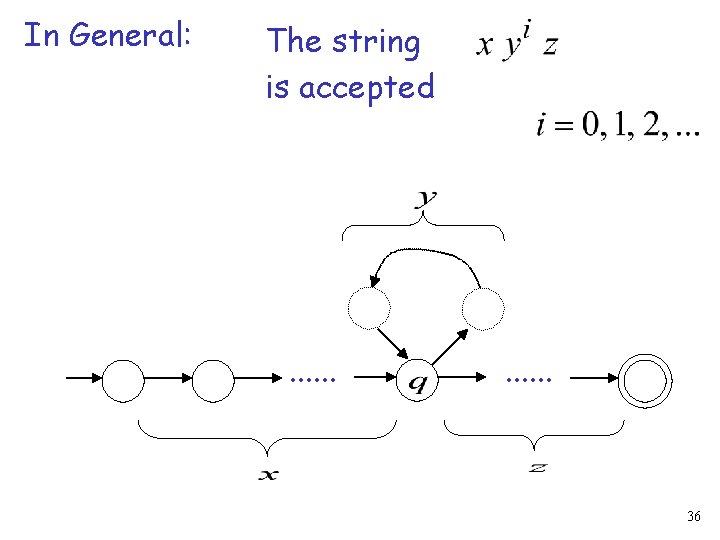
Observation: The string is accepted . . . 35

In General: The string is accepted . . . 36

In other words, we described: The Pumping Lemma 37

The Pumping Lemma: 1. Given a infinite regular language 2. There exists an integer 3. For any string with length 4. We can write 5. With and 6. Such that: string 38

Applications of the Pumping Lemma 39

Claim: The language is not regular Proof: Use the Pumping Lemma 40

Proof: Assume for contradiction that is a regular language Since is infinite we can apply the Pumping Lemma 41

Let be the integer in the Pumping Lemma Pick a string such that: length Example: pick 42

Write From the Pumping Lemma it must be that length Therefore: 43

From the Pumping Lemma: Thus: 44

Therefore, BUT: and CONTRADICTION!!! 45

Therefore: Our assumption that is a regular language cannot be true CONCLUSION: is not a regular language 46

Claim: The language is not regular Proof: Use the Pumping Lemma 47

Proof: Assume for contradiction that is a regular language Since is infinite we can apply the Pumping Lemma 48

Let be the integer in the Pumping Lemma Pick a string such that: length Example: pick 49

Write From the Pumping Lemma it must be that length Therefore: 50
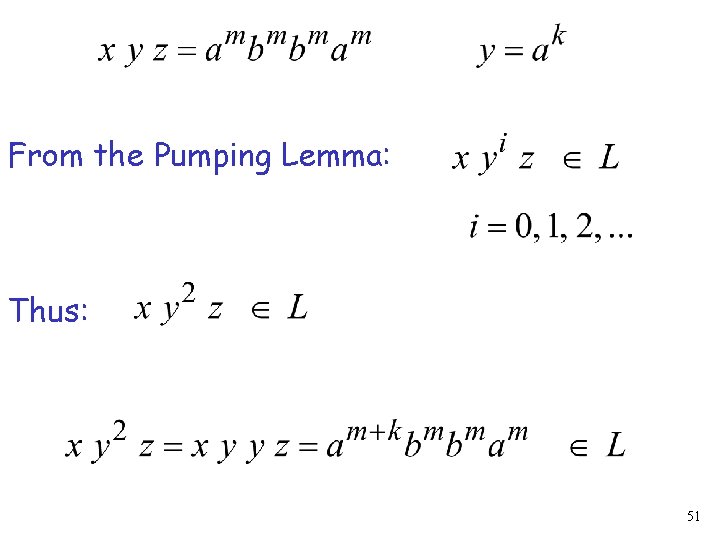
From the Pumping Lemma: Thus: 51

Therefore, BUT: and CONTRADICTION!!! 52

Therefore: Our assumption that is a regular language cannot be true CONCLUSION: is not a regular language 53
 Nfas are ___ dfas.
Nfas are ___ dfas. Verb to be
Verb to be Regular grammars generate regular languages.
Regular grammars generate regular languages. Dfas organizational chart
Dfas organizational chart Nih dfas
Nih dfas Dfas fein
Dfas fein Decision properties of regular languages
Decision properties of regular languages Right linear grammar
Right linear grammar Cs
Cs Decision properties of regular languages
Decision properties of regular languages Decision properties of regular languages
Decision properties of regular languages Decision properties of regular language
Decision properties of regular language Properties of regular languages
Properties of regular languages Closure properties of regular expression
Closure properties of regular expression Regular and irregular languages
Regular and irregular languages Pumping lemma non regular languages examples
Pumping lemma non regular languages examples What is internal benchmarking
What is internal benchmarking Let's watch a video
Let's watch a video Lets go hudro
Lets go hudro The word-skipping technique lets you figure out
The word-skipping technique lets you figure out Let's reported speech
Let's reported speech Offercore nedir
Offercore nedir Let's spread the word
Let's spread the word Lets revisit
Lets revisit The lets
The lets Lets review
Lets review Get ready for
Get ready for 7 horse optical illusion answer
7 horse optical illusion answer Let's answer
Let's answer Lets remember
Lets remember Lets play bridge
Lets play bridge Let’s fight it together
Let’s fight it together Lets see what you already know
Lets see what you already know Progressive lets
Progressive lets Lets make waves
Lets make waves Evolution english language
Evolution english language Youth unit
Youth unit Description of a person
Description of a person Lets livingston county
Lets livingston county Lets have a recap
Lets have a recap Company slogan here
Company slogan here Lets get started images
Lets get started images Lets move on
Lets move on Warm up questions about travelling
Warm up questions about travelling Lets review cartoon
Lets review cartoon Let's play jeopardy
Let's play jeopardy Paper that lets the light shine through
Paper that lets the light shine through Lets play
Lets play Let's do the rooms
Let's do the rooms Let's go lesson plans
Let's go lesson plans Let's clean together
Let's clean together Lets see what you know
Lets see what you know Lets review
Lets review We're free let's grow answer key
We're free let's grow answer key