Lets Go Buy a Computer So Whats in

Let’s Go Buy a Computer

So What’s in a Computer? • • Processor brains Memory scratch paper Disk long term memory I/O communication (senses) • Software reconfigurability

What’s in a Computer? Power Disk RAM CPU Communications Ports Software I/O Text Sound

Putting Together an Application • • • Word (is a part of the Office application) Runs on Windows (an operating system) Which runs on a Dell PC (a computer) Which has a Pentium (a processor) Enhanced by connections to monitor, printer, network Uses random access memory (RAM) to work on document, disk (non-volatile) memory to store in • Need a CD-ROM to install application (or install off the Internet over a broadband connection)

Let’s Go Buy a Computer

Computer Configuration • • Processor (Pentium IV, 2. 8 GHz) RAM (512 MB of SDRAM (expandable)) Disk (80 GB) CD ROM/ CD RW/DVD/… 17" XGA TFT Display (1280 x 1024 res. ) 3. 5" 1. 44 MB Floppy Disk Drive S 3 Savage IX 128 -bit AGP 2 x graphics – 8 MB memory, 3 D Hardware acceleration, composite TV-Out support, … • 16 -bit Sound

Computer Configuration (contd) • • 2 Type-I or Type-II slots or 1 Type-III slot 2 USB Ports Built-in 56 Kbps V. 90 Data/fax modem Built-in 10/100 Ethernet Adapter and 802. 11 b/g wireless • Also – universal AC adapter, – built-in Lithium-Ion battery, – Microsoft Windows XP, – Encarta World Encyclopedia online version…

What’s Special About a Computer? • • • Most complex object made by humans A rich communication mechanism for society Amazing how it works Reconfigurability Moore’s Law

More for Less --Moore’s Law • 1985 when I was a student here – A desktop machine in the lab • • $150, 000 (now < $1, 000) 700 KHz chip (now ~3 GHz) 1 MB memory (now 128 -512 MB) 80 MB disk (now 80 GB +) CD-ROM had just been invented (83) Minimal Internet connection Communication to Internet 9600 bps (now 10 Mbps)

Moore’s Law (contd) • $150, 000 (now < $1, 000) – Factor of 150 • 700 Khz processor (now 2 GHz chip) – Factor of 3000 • 1 MB memory (now 256 MB) – Factor of 256 • 80 MB disk (now 40/80 GB) – Factor of 1000 • Communication 9600 bps (now 10 Mbps) – Factor of 1000

An interesting example: Walmart/Microtel PC • • • AMD 1. 5 GHz Sempron processor with 3 DNow! Technology 128 MB DDR Memory, expandable to 2 GB 20 GB Ultra ATA-100 Hard Drive / 5400 RPM 52 x CD-ROM drive Integrated 10/100 Ethernet Connection Integrated graphics up to 64 MB shared video memory Integrated 5. 1 Channel AC'97 Audio Available drive bays: Two 5. 25", one 3. 5“ No operating system installed Speakers, but no display • Price: $198

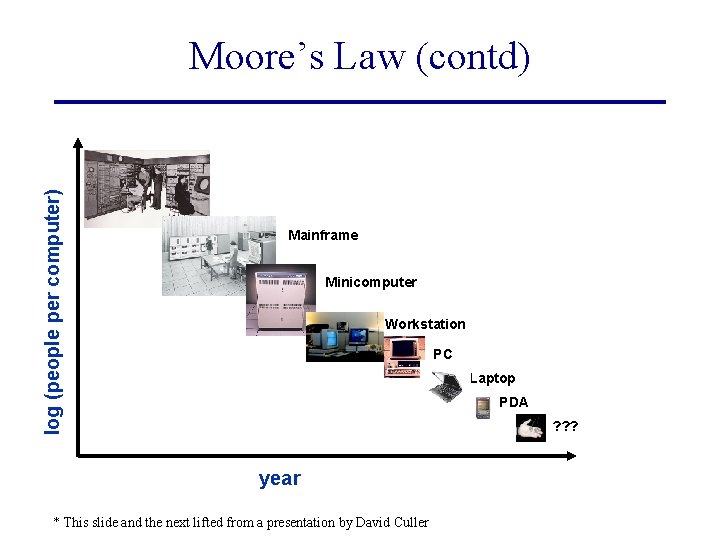
log (people per computer) Moore’s Law (contd) Mainframe Minicomputer Workstation PC Laptop PDA ? ? ? year * This slide and the next lifted from a presentation by David Culler

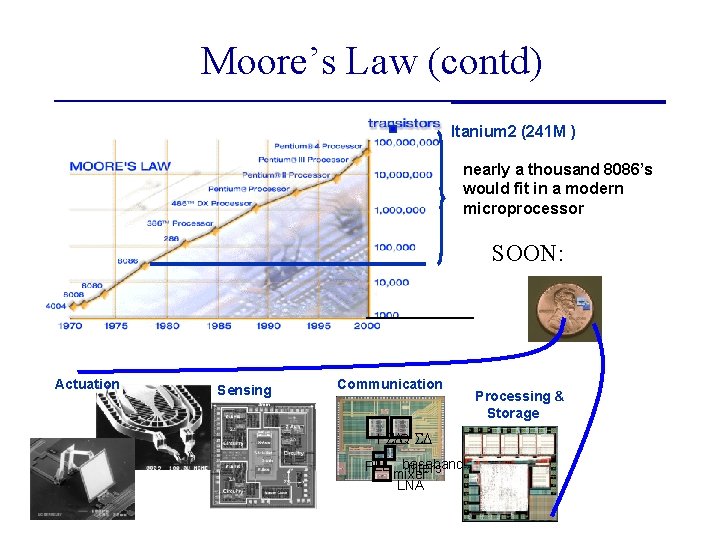
Moore’s Law (contd) Itanium 2 (241 M ) nearly a thousand 8086’s would fit in a modern microprocessor SOON: Actuation Sensing Communication I SDQ SD PLL baseband filters mixer LNA Processing & Storage

Rest of the Course • Hardware: Building a computer – – How arithmetic and logical operations are realized How data are represented How memory is realized How sequencing is done and state machines are realized • Software: Programming and Using a computer – Programs and Programming languages – Algorithms – Applications: Graphics and Sound • Operating Systems, Networking and Distributed Computing – – Operating Systems Basic Networking Applications: E-mail and the Internet Peer-to-peer and music sharing • Hard Problems and Limits of Computing • Security, Privacy, Artificial Intelligence (? )

Let’s Build a Computer

Building a computer Really Simple Stuff

Why build a computer? • Curiosity – What really happens when I hit a key? • Necessity – Prerequisite to parts of the course • Breadth – Should understand what’s changing the world

Why NOT build a computer? • Computers seem really complicated – Pentium IV chip has 42 million transistors – (in an area of 217 square mm, ) • How can we hope to understand them ?

Analogy with Building a House • • Components Glue for combining components Modeling the process Tools and Rules In fact, computer design is called computer architecture

Questions in Building a House • What are the basic components – 2”x 4”’s, I-beams, plasterboard, . . – Light fixtures, plumbing, … • What is glue for combining them – Nails, screws, bolts, pipes, … • How do we model the process – Architectural drawings, building codes, …

Questions in Building a Computer • What are the basic components – Logic gates • What is glue for combining them – Wires to build circuits • How do we model the process – Architectural drawings, design rules, … – Mathematical formulation

Details • Wires are made of silicon or other chemicals • Crossing wires implement transistors, the basic unit of computer design • Transistors control the flow of electrons (current) – They either do or don’t flow through – Think of light switches turning current on or off • Wire thickness is currently about. 1 micron – 1 micron = 10 -6 meters – Can fit 42 million transistors in less than 1. 5 cmx 1. 5 cm • Design must follow fabrication rules – Wires can’t get too close (unless they cross) • A key tool is abstraction

What is Abstraction? • Ignoring or hiding details to capture essential features for the purpose at hand • E. g. we’ll ignore whether we’re talking about: – A Pentium II or a Pentium III – A Mac or a PC • Instead, we’ll focus on what really makes a computer.

Abstraction in Everyday Life • Parent says: “Brush your teeth” • Parent doesn’t specify: – – What kind of toothbrush What kind of toothpaste What you’re wearing etc. • These things aren’t important to the order at hand

Abstraction (cont. ) • If we had to spell out everything in full detail, our lives would be really complicated • Abstraction allows us to understand things in a modular fashion • Same is true for computers: To understand them, we use abstraction

It’s Not 100 Million Transistors • It’s a few major functional components – Each exposes a functional interface – They’re connected to one another with wires • Each is composed of a number of smaller components – Each of which exposes a functional interface – They’re connected to one another with wires • And so on, until each is composed of a few transistors – There’s usually a lot of regularity among these (many similar building blocks)

Layers of Abstraction Really Simple Stuff Computers • Build more powerful tools out of simpler ones • What’s the really simple stuff? – 0 s and 1 s

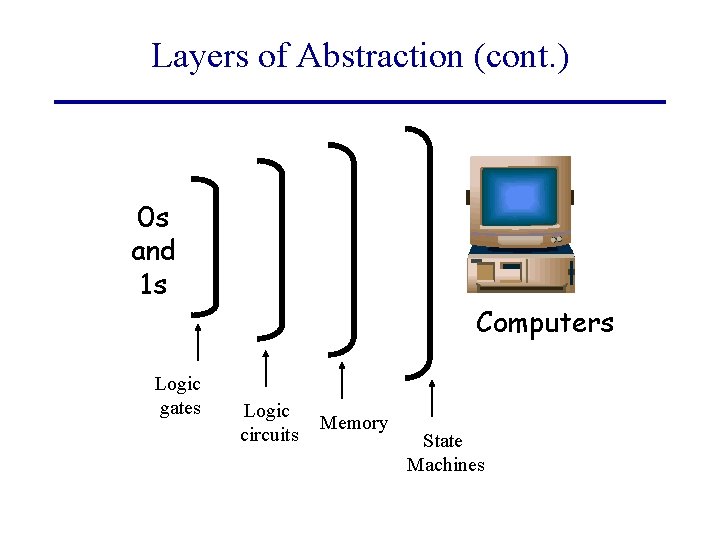
Layers of Abstraction (cont. ) 0 s and 1 s Logic gates Computers Logic circuits Memory State Machines

Logic and Logic Gates

A Simple Logic Puzzle • Frank will go to the party if Ed goes AND Dan does NOT. • Dan will go if Bob does NOT go OR if Carole goes. • Ed will go to the party if Alice AND Bob go. • Alice and Bob decide to go, but Carol stays home. • Will Frank go to the party? • Answer: YES

Using 0 s and 1 s • • What do 0’s and 1’s mean? For now, we’ll take “Natural meanings: ” 0 = False • 1 = True For example, if we have a variable ‘Alice’ that denotes whether Alice goes to the party, • If Alice goes, we say Alice = 1 • If Alice doesn’t, we say Alice = 0

Logic Gates • Computers are circuits made of Logic Gates. • Logic gates manipulate 0’s and 1’s (False and True) by letting electrons flow or not. • We’ll look at three types of Logic Gates: • AND are all inputs true? • OR is at least one input true? • NOT flip the truth value

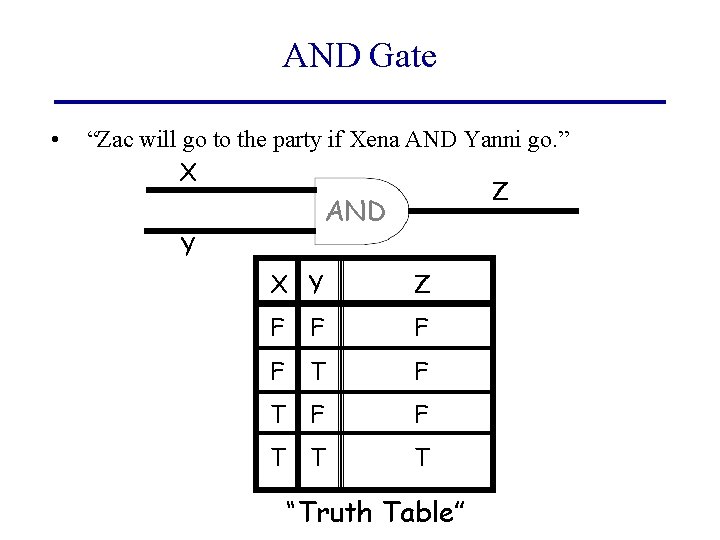
AND Gate • “Zac will go to the party if Xena AND Yanni go. ” X Z AND Y X Y Z F F T T T “Truth Table”

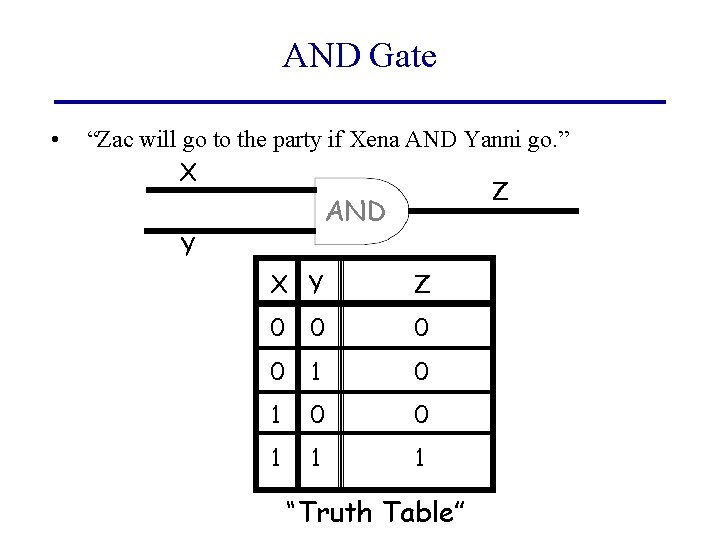
AND Gate • “Zac will go to the party if Xena AND Yanni go. ” X Z AND Y X Y Z 0 0 1 1 1 “Truth Table”

AND Gate (contd) • AND Gate is a circuit that allows output current to flow if both inputs are flowing – i. e. output is 1 if and only if both inputs are 1

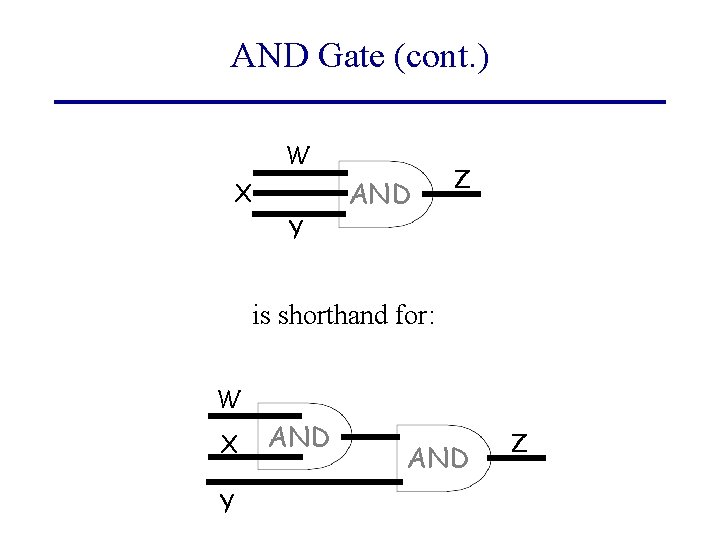
AND Gate (cont. ) W X Y AND Z is shorthand for: W X Y AND Z

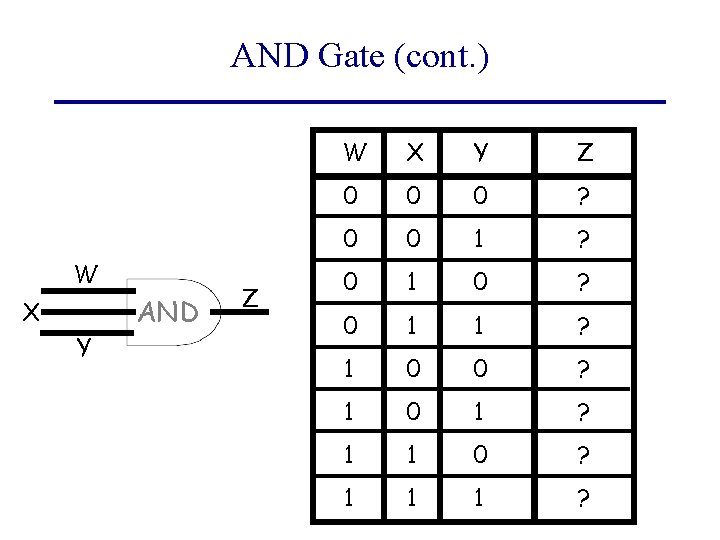
AND Gate (cont. ) W X Y AND Z W X Y Z 0 0 0 ? 0 0 1 ? 0 1 0 ? 0 1 1 ? 1 0 0 ? 1 0 1 ? 1 1 0 ? 1 1 1 ?

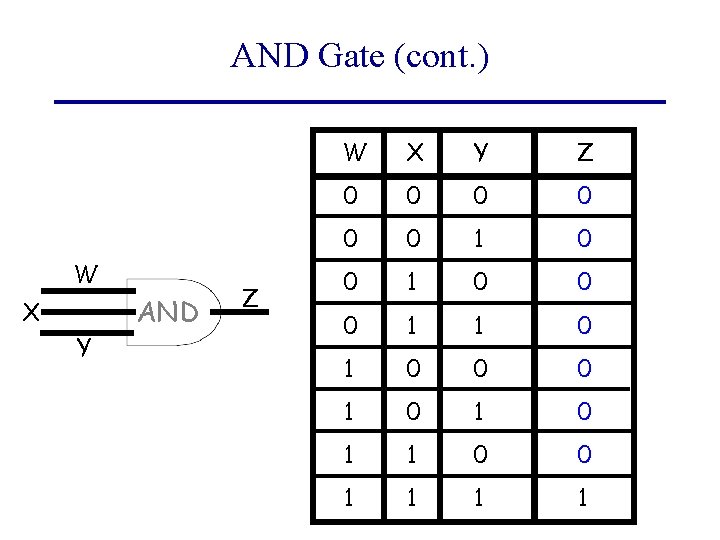
AND Gate (cont. ) W X Y AND Z W X Y Z 0 0 0 1 1 0 0 0 1 0 1 1 0 0 1 1

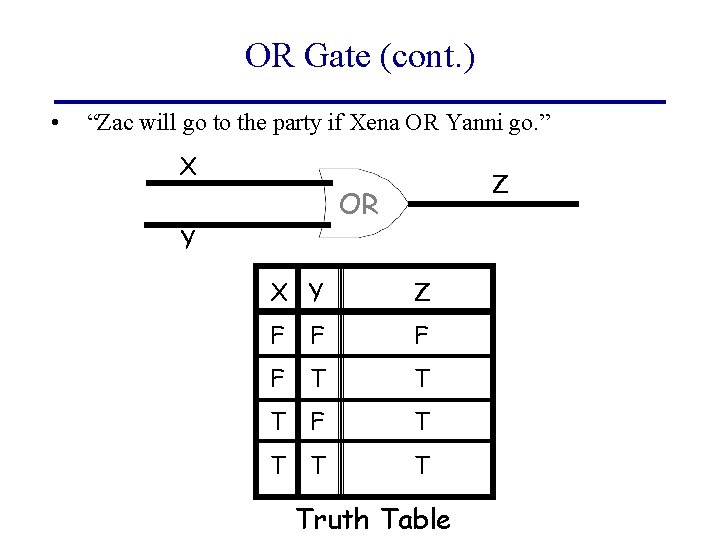
OR Gate (cont. ) • “Zac will go to the party if Xena OR Yanni go. ” X Z OR Y X Y Z F F T T Truth Table

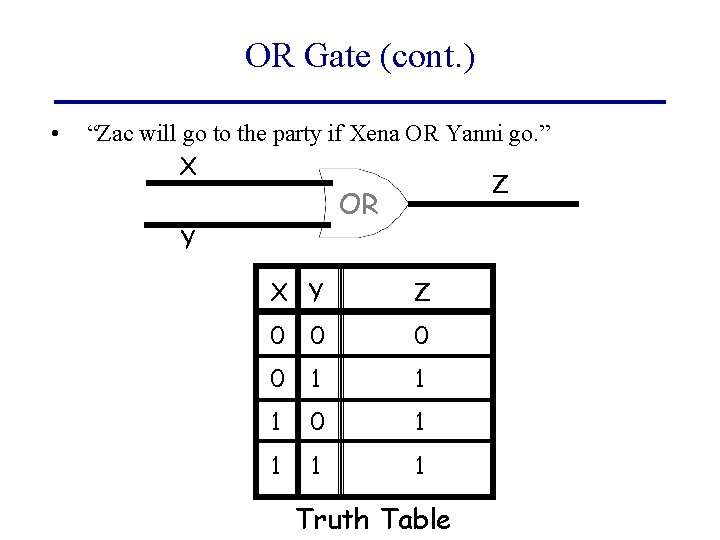
OR Gate (cont. ) • “Zac will go to the party if Xena OR Yanni go. ” X Z OR Y X Y Z 0 0 1 1 1 0 1 1 Truth Table

OR Gate (contd) • OR Gate is a circuit that allows output current to flow if either input is flowing – i. e. output is 1 if either input is 1 (or both inputs are 1)

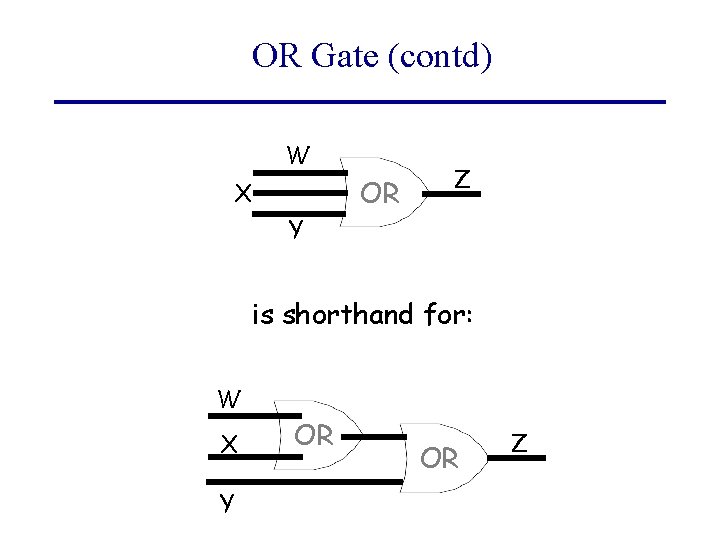
OR Gate (contd) W OR X Z Y is shorthand for: W X Y OR OR Z

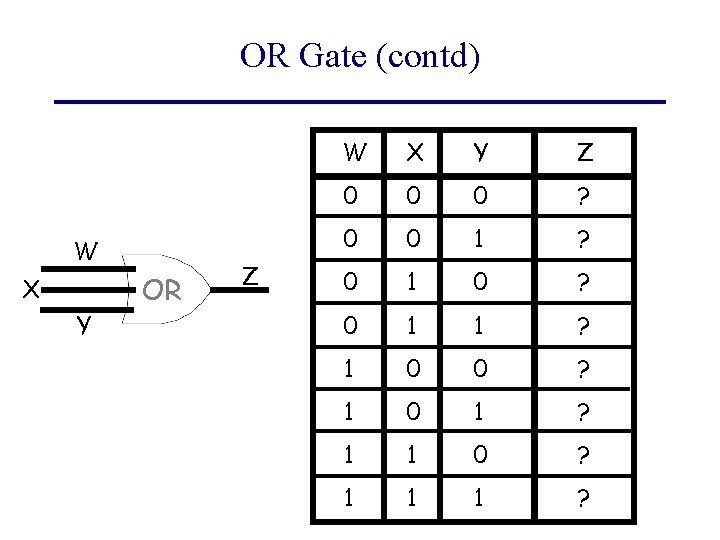
OR Gate (contd) W X Y OR Z W X Y Z 0 0 0 ? 0 0 1 ? 0 1 0 ? 0 1 1 ? 1 0 0 ? 1 0 1 ? 1 1 0 ? 1 1 1 ?

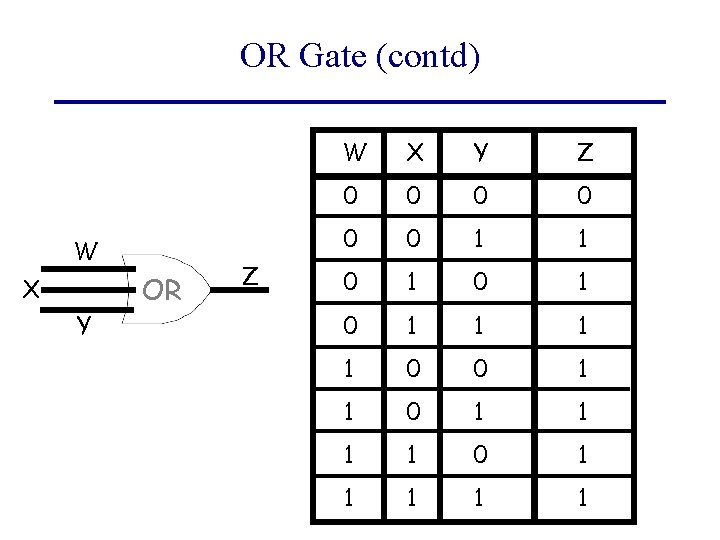
OR Gate (contd) W X Y OR Z W X Y Z 0 0 0 1 1 0 1 0 1 1 0 0 1 1 1 1 0 1 1 1

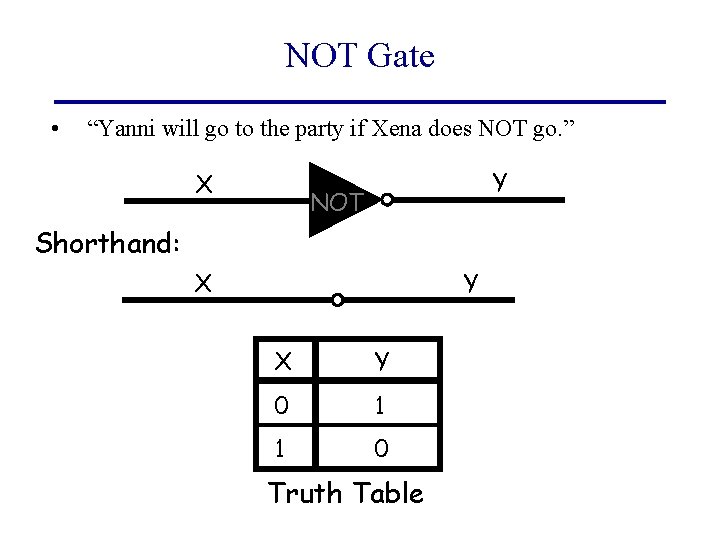
NOT Gate • “Yanni will go to the party if Xena does NOT go. ” X Y NOT Shorthand: Y X X Y 0 1 1 0 Truth Table

NOT Gate (contd) • NOT Gate is a circuit that reverses the sense of a flow. – i. e. Logical complement: Output is 1 if and only if input is 0

Back to Our Simple Logic Puzzle • Frank will go to the party if Ed goes AND Dan does NOT. • Dan will go if Bob does NOT go OR if Carole goes. • Ed will go to the party if Alice AND Bob go. • Alice and Bob decide to go, but Carol stays home. • Will Frank go to the party?

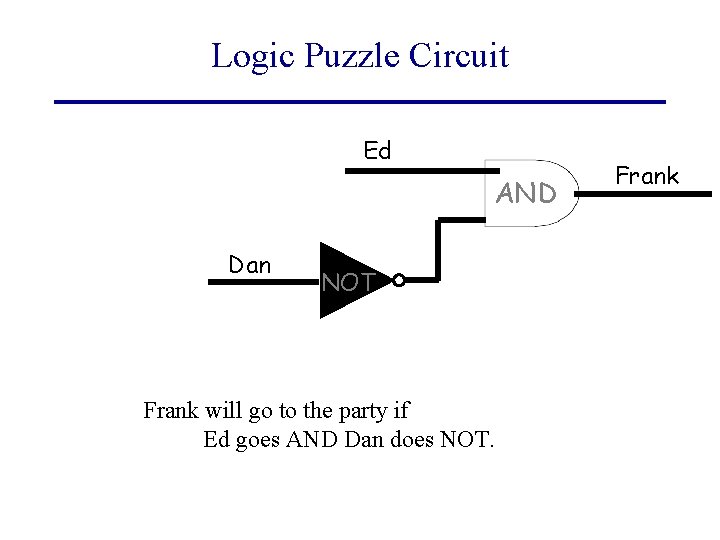
Logic Puzzle Circuit Ed AND Dan NOT Frank will go to the party if Ed goes AND Dan does NOT. Frank

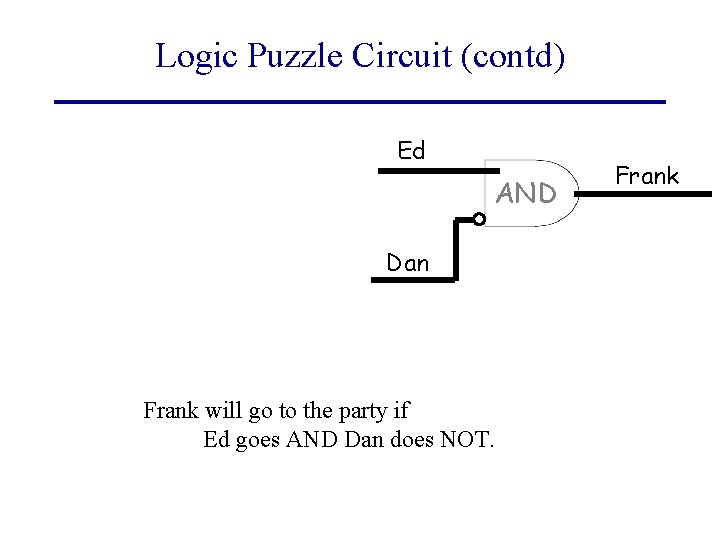
Logic Puzzle Circuit (contd) Ed AND Dan Frank will go to the party if Ed goes AND Dan does NOT. Frank

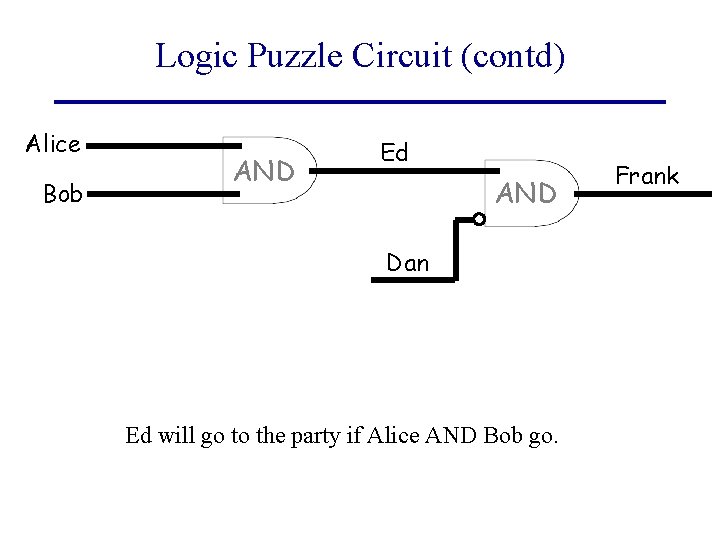
Logic Puzzle Circuit (contd) Alice Bob AND Ed AND Dan Ed will go to the party if Alice AND Bob go. Frank

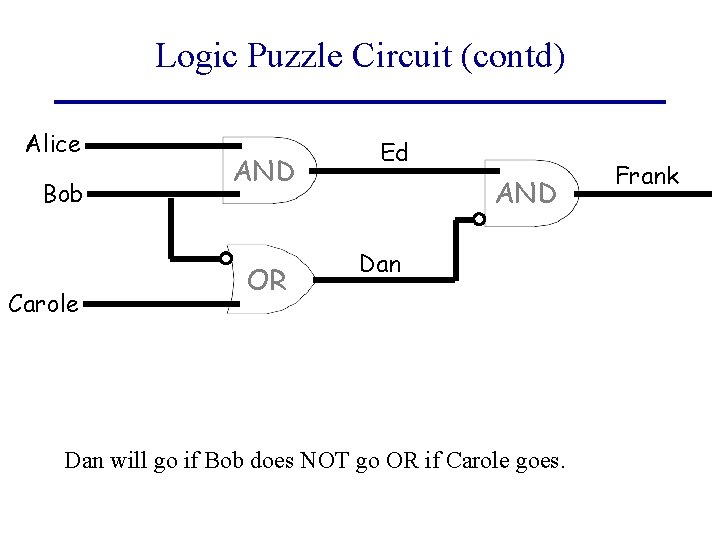
Logic Puzzle Circuit (contd) Alice Bob Carole AND OR Ed AND Dan will go if Bob does NOT go OR if Carole goes. Frank

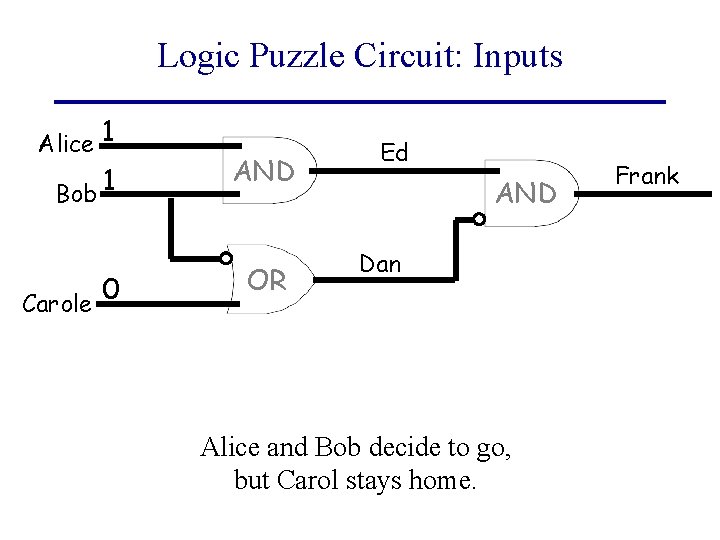
Logic Puzzle Circuit: Inputs Alice 1 Bob 1 0 Carole AND OR Ed AND Dan Alice and Bob decide to go, but Carol stays home. Frank

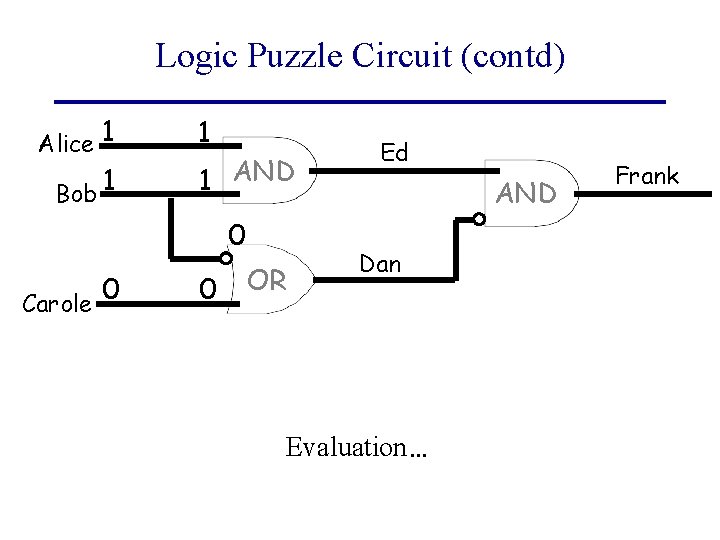
Logic Puzzle Circuit (contd) Alice 1 Bob 1 1 1 AND 0 0 Carole 0 OR Ed AND Dan Evaluation… Frank

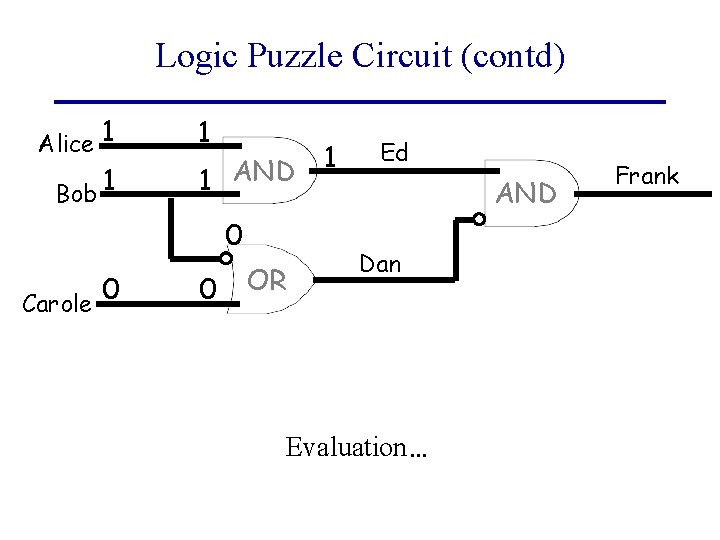
Logic Puzzle Circuit (contd) Alice 1 Bob 1 1 1 AND 0 0 Carole 0 OR 1 Ed AND Dan Evaluation… Frank

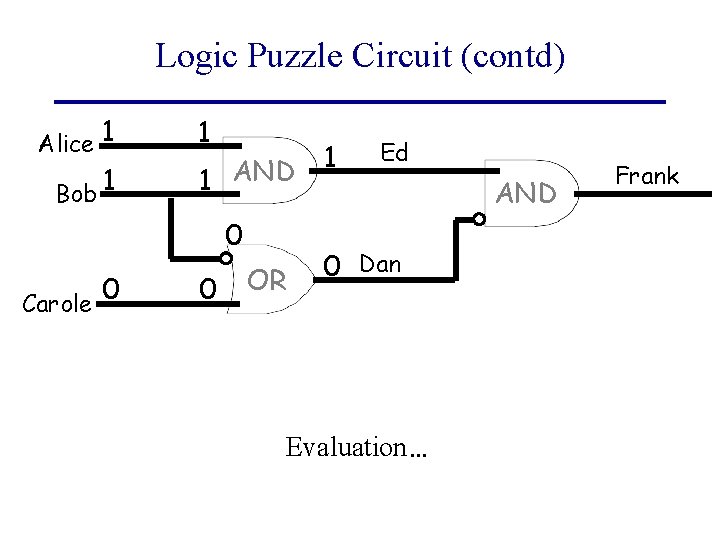
Logic Puzzle Circuit (contd) Alice 1 Bob 1 1 1 AND 0 0 Carole 0 OR 1 Ed 0 Dan Evaluation… AND Frank

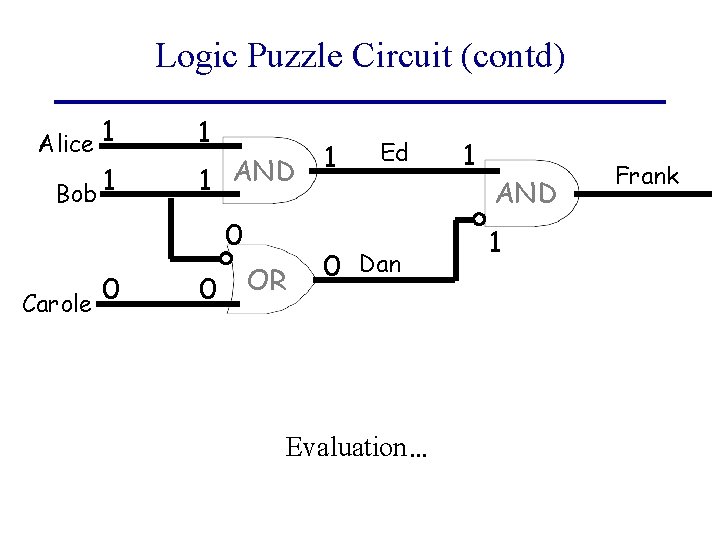
Logic Puzzle Circuit (contd) Alice 1 Bob 1 1 1 AND 0 0 Carole 0 OR 1 Ed 0 Dan Evaluation… 1 AND 1 Frank

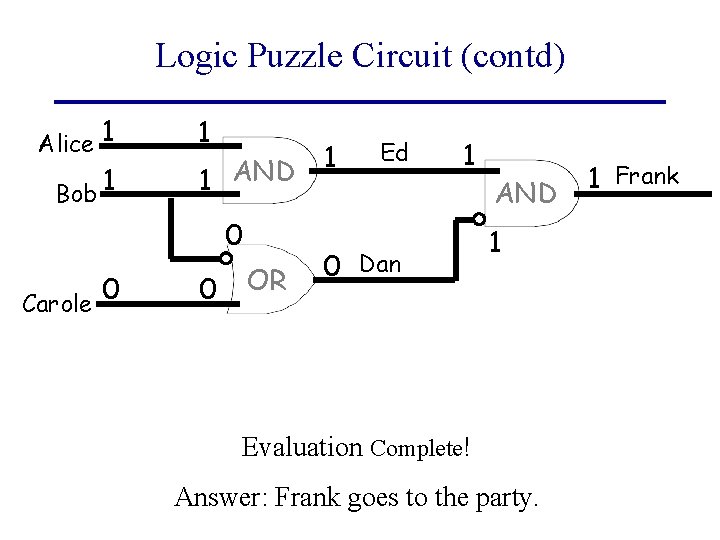
Logic Puzzle Circuit (contd) Alice 1 Bob 1 1 1 AND 0 0 Carole 0 OR 1 Ed 1 0 Dan AND 1 Evaluation Complete! Answer: Frank goes to the party. 1 Frank

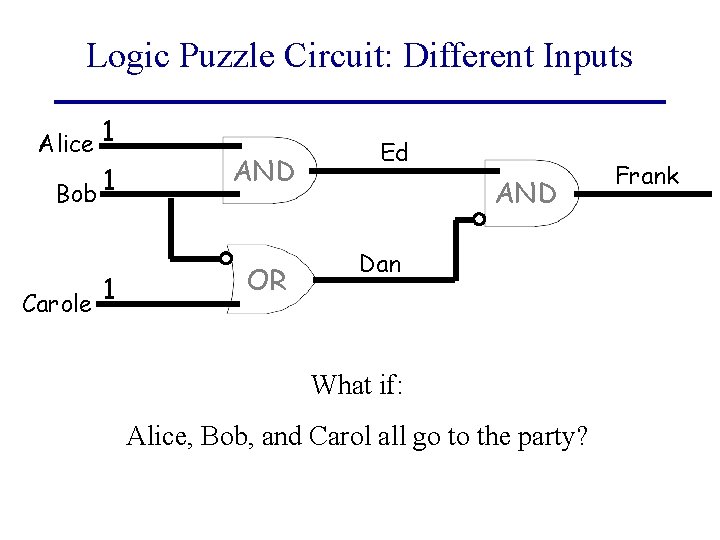
Logic Puzzle Circuit: Different Inputs Alice 1 Bob 1 1 Carole AND OR Ed AND Dan What if: Alice, Bob, and Carol all go to the party? Frank

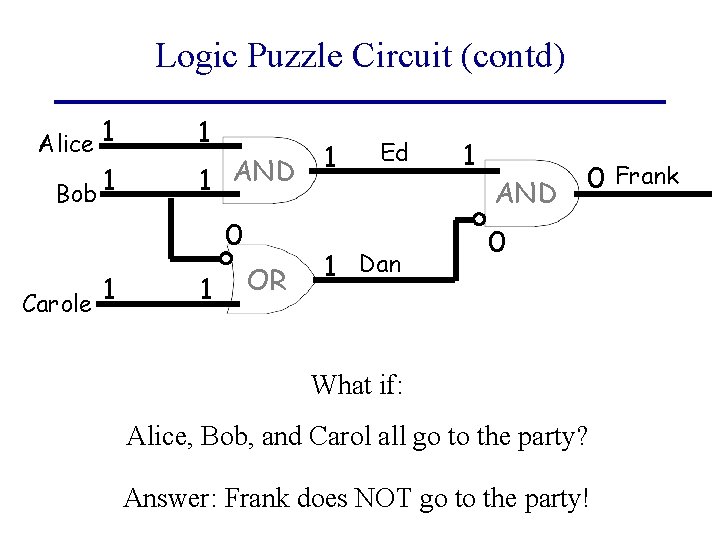
Logic Puzzle Circuit (contd) Alice 1 Bob 1 1 1 AND 0 1 Carole 1 OR 1 Ed 1 Dan 1 AND 0 Frank 0 What if: Alice, Bob, and Carol all go to the party? Answer: Frank does NOT go to the party!

All Clear?

Building Circuits • Suppose someone gives us an arbitrary Truth Table. • How do we build a circuit which satisfies exactly that Truth Table?

Our Friend the Logic Puzzle • Frank will go to the party if Ed goes AND Dan does NOT. • Dan will go if Bob does NOT go OR if Carole goes. • Ed will go to the party if Alice AND Bob go. • Let’s start with the Truth Table instead

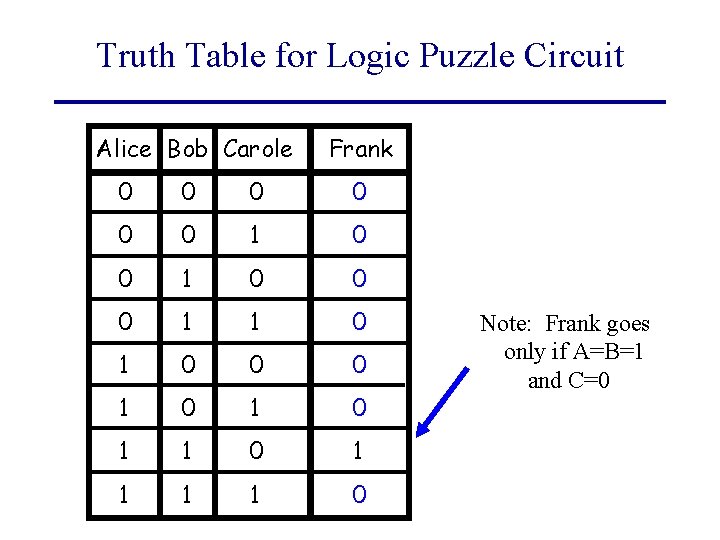
Truth Table for Logic Puzzle Circuit Alice Bob Carole Frank 0 0 0 1 1 0 0 0 1 0 1 1 1 1 0 Note: Frank goes only if A=B=1 and C=0

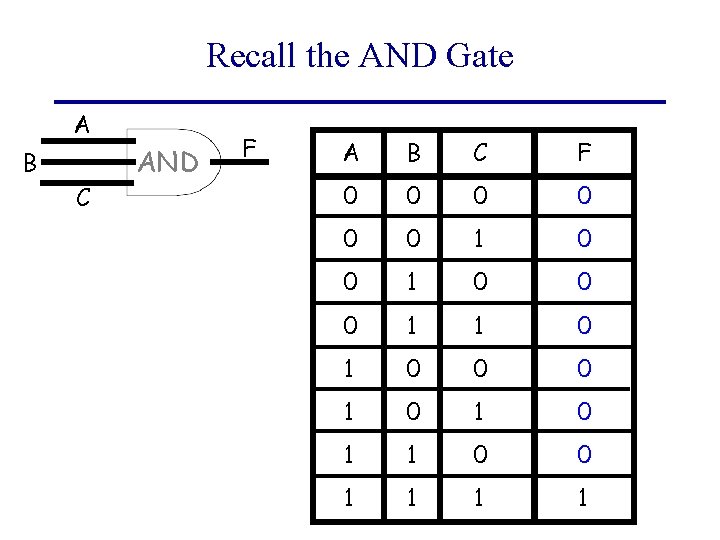
Recall the AND Gate A B C AND F A B C F 0 0 0 1 1 0 0 0 1 0 1 1 0 0 1 1

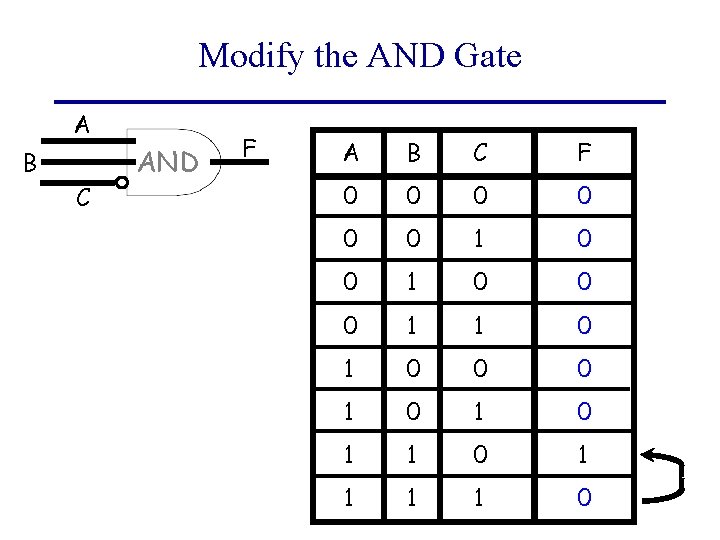
Modify the AND Gate A B C AND F A B C F 0 0 0 1 1 0 0 0 1 0 1 1 1 1 0

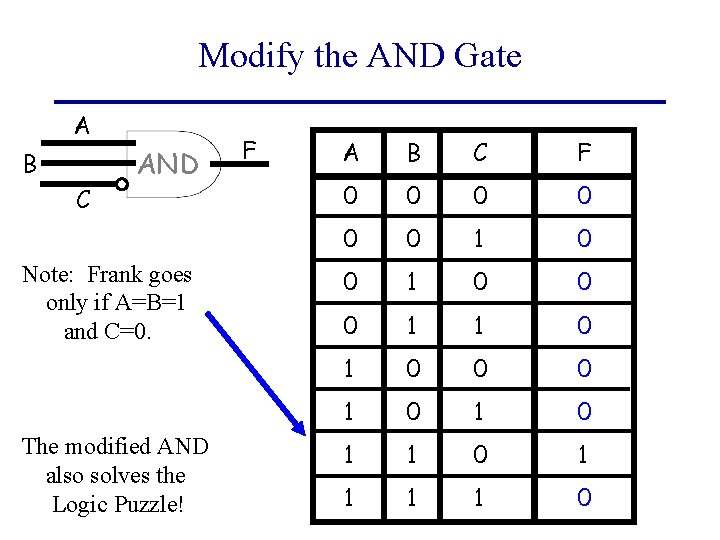
Modify the AND Gate A B C AND Note: Frank goes only if A=B=1 and C=0. The modified AND also solves the Logic Puzzle! F A B C F 0 0 0 1 1 0 0 0 1 0 1 1 1 1 0

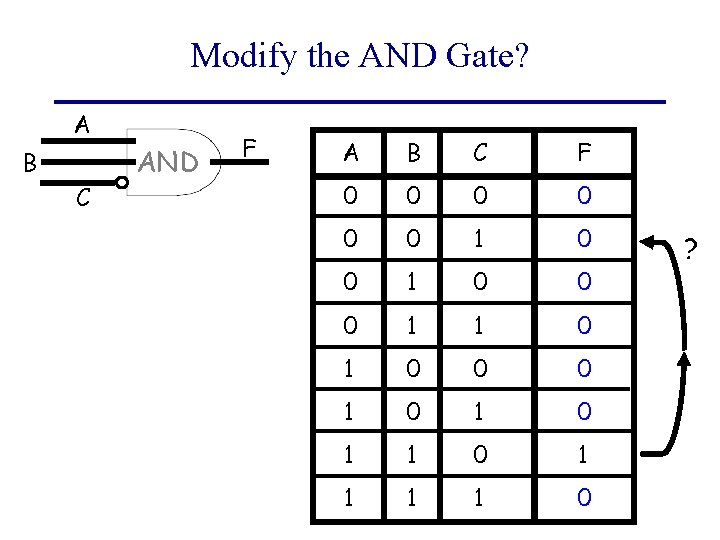
Modify the AND Gate? A B C AND F A B C F 0 0 0 1 1 0 0 0 1 0 1 1 1 1 0 ?

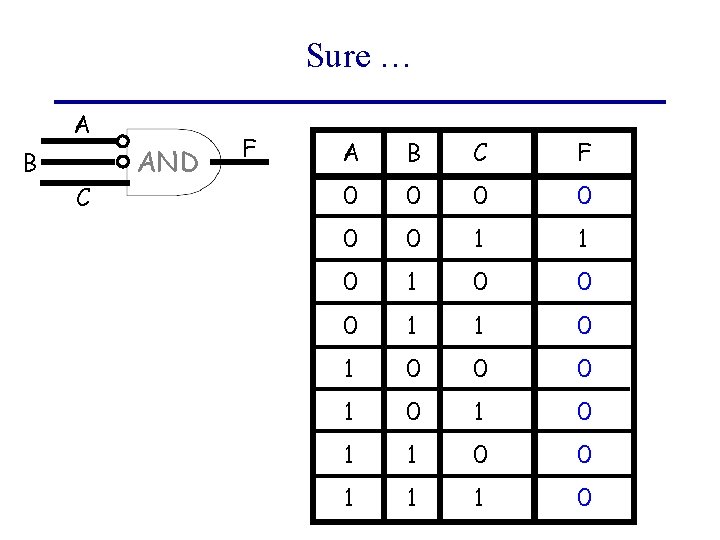
Sure … A B C AND F A B C F 0 0 0 1 1 0 1 0 0 0 1 0 1 1 0 0 1 1 1 0

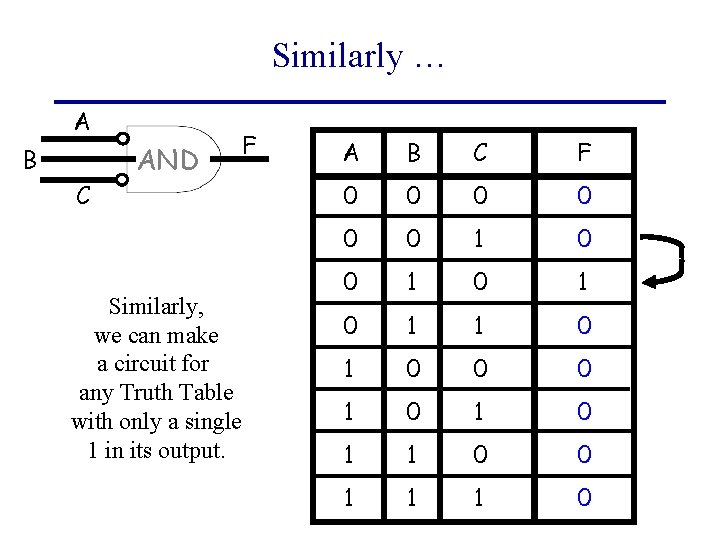
Similarly … A B C AND Similarly, we can make a circuit for any Truth Table with only a single 1 in its output. F A B C F 0 0 0 1 0 1 1 0 0 0 1 0 1 1 0 0 1 1 1 0

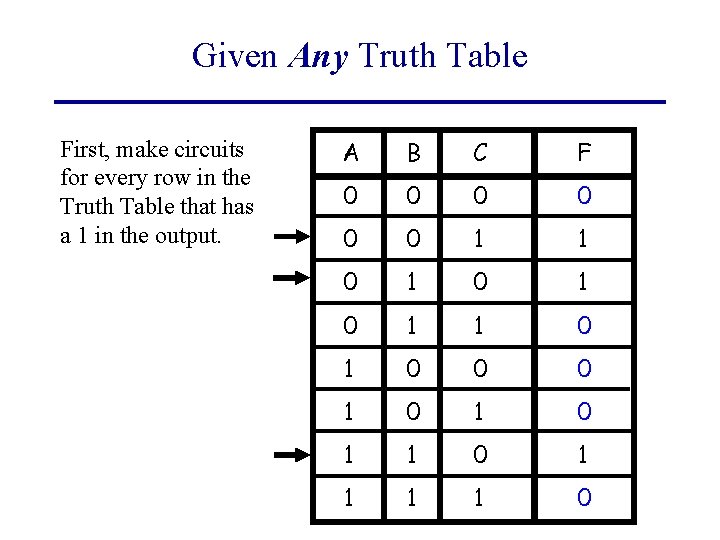
Given Any Truth Table First, make circuits for every row in the Truth Table that has a 1 in the output. A B C F 0 0 0 1 1 0 1 0 1 0 0 0 1 0 1 1 1 1 0

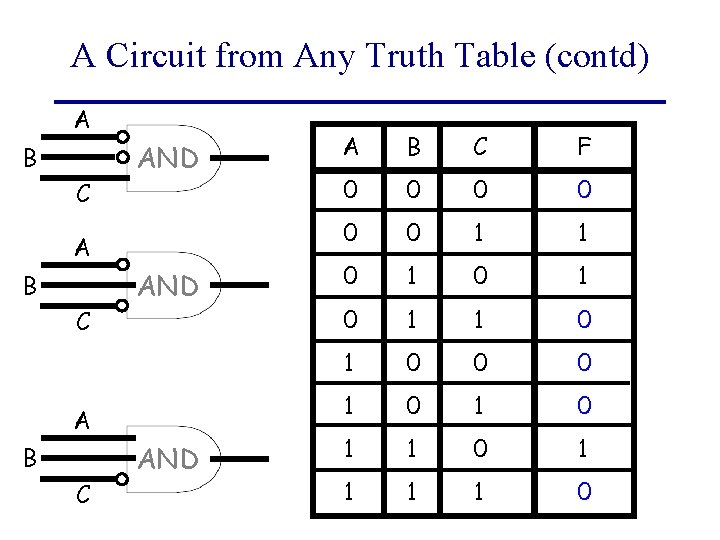
A Circuit from Any Truth Table (contd) A B C AND A B C F 0 0 0 1 1 0 1 0 1 0 0 0 1 0 1 1 1 1 0

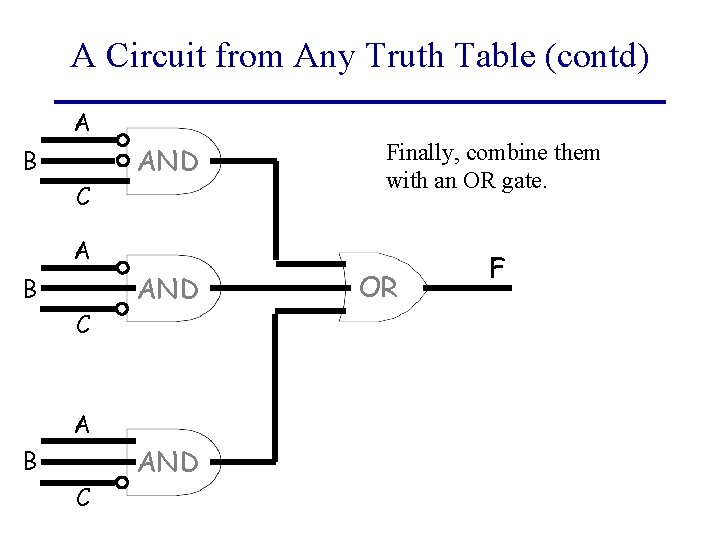
A Circuit from Any Truth Table (contd) A B C AND Finally, combine them with an OR gate. A B C AND OR F

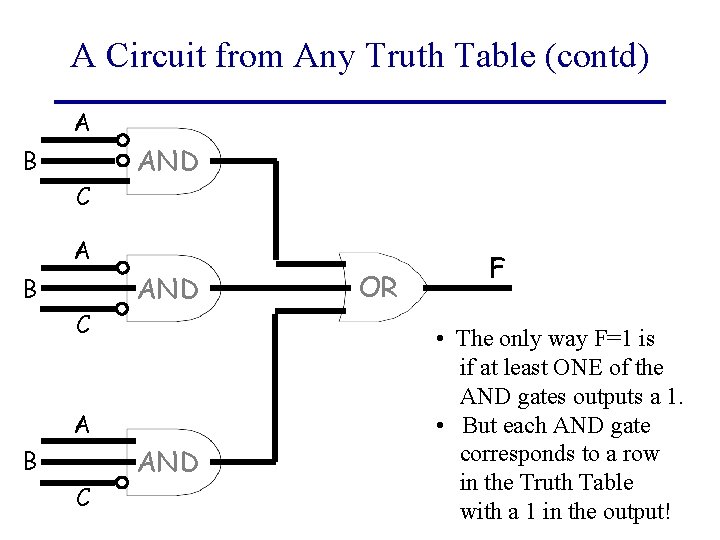
A Circuit from Any Truth Table (contd) A B C AND OR F • The only way F=1 is if at least ONE of the AND gates outputs a 1. • But each AND gate corresponds to a row in the Truth Table with a 1 in the output!

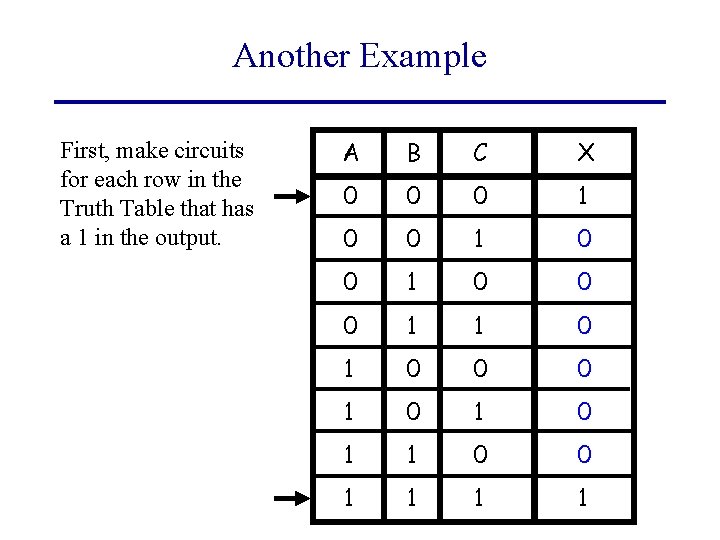
Another Example First, make circuits for each row in the Truth Table that has a 1 in the output. A B C X 0 0 0 1 0 0 0 1 1 0 0 0 1 0 1 1 0 0 1 1

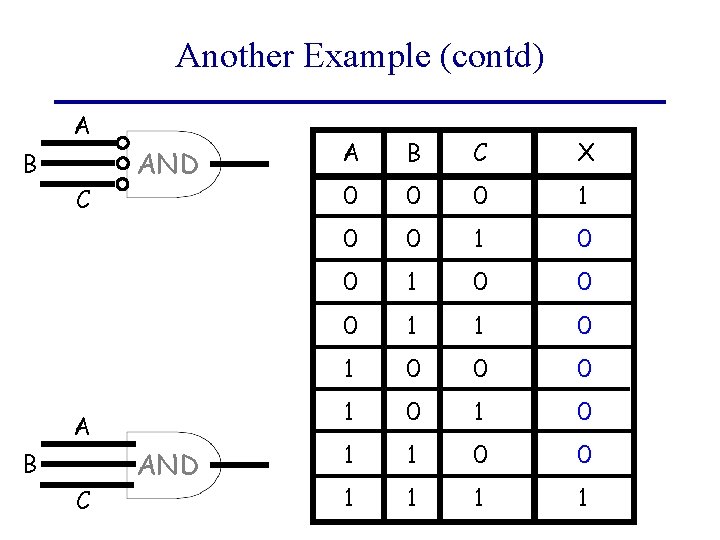
Another Example (contd) A B C AND A B C X 0 0 0 1 0 0 0 1 1 0 0 0 1 0 1 1 0 0 1 1

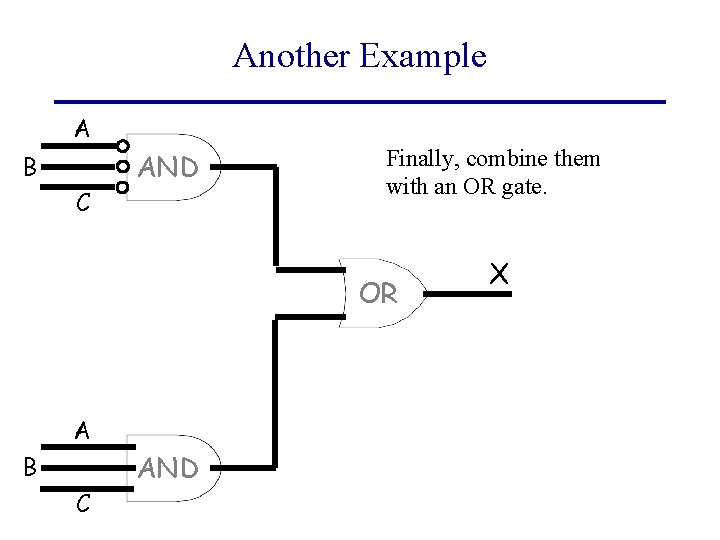
Another Example A B C AND Finally, combine them with an OR gate. OR A B C AND X

Universality • Same idea works no matter how many input variables. • So for ANY Truth Table we can write down, we can make a circuit for it using only 3 Logic Gates: AND, OR, NOT • This gives us a very powerful tool ! • Our first technical use of abstraction: “Make a circuit for that Truth Table” is something we can abstract and understand.

Additional Issues Some issues to think about on your own • We know that AND, OR, and NOT together are “universal” – we can make a circuit for any Truth Table using just these gates ! What else is universal? • Surprising answer: There is a single gate called “NAND” which is universal all by itself!

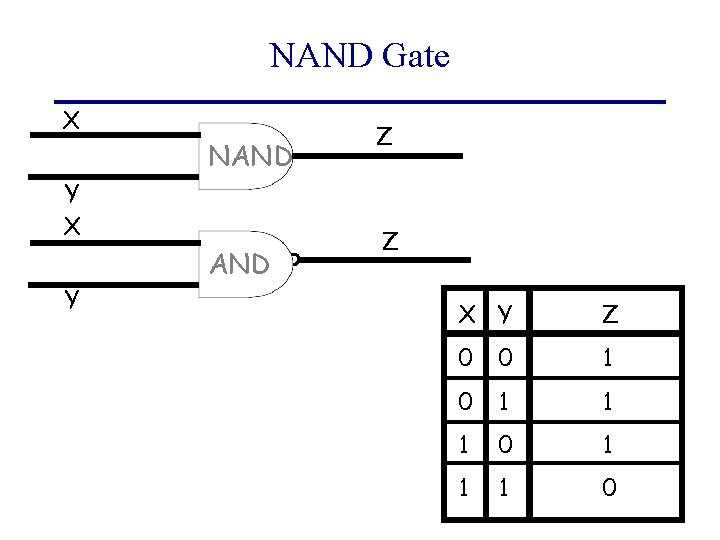
NAND Gate X NAND Y X Y AND Z Z X Y Z 0 0 1 1 1 0

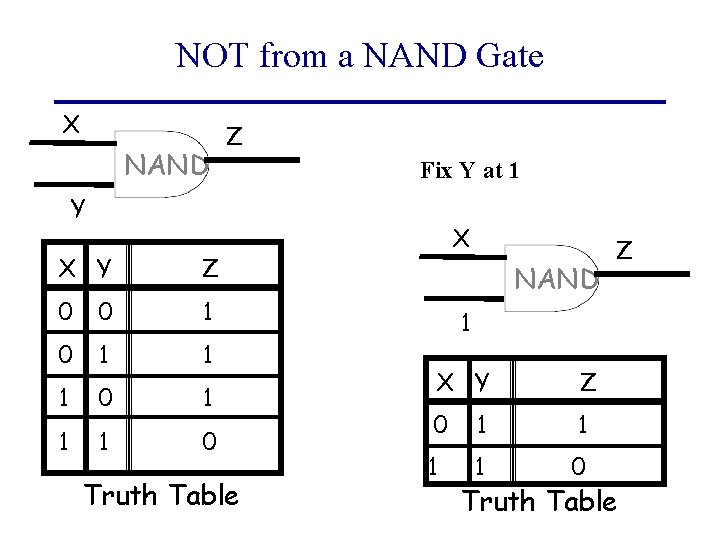
NOT from a NAND Gate X NAND Z Fix Y at 1 Y X Y Z 0 0 1 1 1 0 Truth Table X NAND Z 1 X Y Z 0 1 1 0 Truth Table

Additional Issues Some issues to think about on your own: We saw two circuits for the Logic Puzzle that both worked – but one (the modified AND) was much simpler than the other. • Can you come up with methods for simplifying circuits? • This is important for efficiency when you are dealing with very large Truth Tables (which we will see in the future).

Are We Done?