Let us discuss the harmonic oscillator Let us























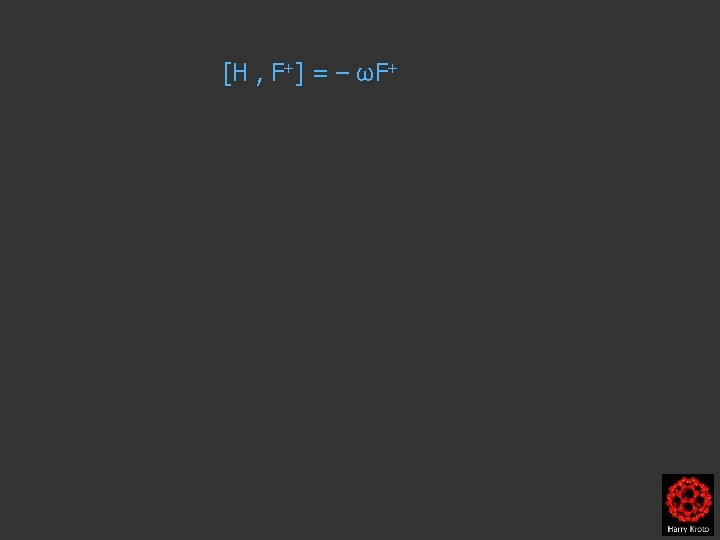

![[H , F+] = – ωF+ HF+ – F+H = – ωF+ Now let’s [H , F+] = – ωF+ HF+ – F+H = – ωF+ Now let’s](https://slidetodoc.com/presentation_image/3863ac9d5172e3e5026bb40d481df4b6/image-26.jpg)
![[H , F+] = – ωF+ HF+ – F+H = – ωF+ Now let’s [H , F+] = – ωF+ HF+ – F+H = – ωF+ Now let’s](https://slidetodoc.com/presentation_image/3863ac9d5172e3e5026bb40d481df4b6/image-27.jpg)
![[H , F+] = – ωF+ HF+ – F+H = – ωF+ Now let’s [H , F+] = – ωF+ HF+ – F+H = – ωF+ Now let’s](https://slidetodoc.com/presentation_image/3863ac9d5172e3e5026bb40d481df4b6/image-28.jpg)
![[H , F+] = – ωF+ HF+ – F+H = – ωF+ Now let’s [H , F+] = – ωF+ HF+ – F+H = – ωF+ Now let’s](https://slidetodoc.com/presentation_image/3863ac9d5172e3e5026bb40d481df4b6/image-29.jpg)
![[H , F+] = – ωF+ HF+ – F+H = – ωF+ Now let’s [H , F+] = – ωF+ HF+ – F+H = – ωF+ Now let’s](https://slidetodoc.com/presentation_image/3863ac9d5172e3e5026bb40d481df4b6/image-30.jpg)
![[H , F+] = – ωF+ HF+ – F+H = – ωF+ Now let’s [H , F+] = – ωF+ HF+ – F+H = – ωF+ Now let’s](https://slidetodoc.com/presentation_image/3863ac9d5172e3e5026bb40d481df4b6/image-31.jpg)
![[H , F+] = – ωF+ HF+ – F+H = – ωF+ Now let’s [H , F+] = – ωF+ HF+ – F+H = – ωF+ Now let’s](https://slidetodoc.com/presentation_image/3863ac9d5172e3e5026bb40d481df4b6/image-32.jpg)


























![[q, p] = i [H, q] = ω(–ip) [H, p] = ω(iq) From this [q, p] = i [H, q] = ω(–ip) [H, p] = ω(iq) From this](https://slidetodoc.com/presentation_image/3863ac9d5172e3e5026bb40d481df4b6/image-60.jpg)
![[H , F+] = – ωF+ HF+ – F+H = – ωF+ Operate on [H , F+] = – ωF+ HF+ – F+H = – ωF+ Operate on](https://slidetodoc.com/presentation_image/3863ac9d5172e3e5026bb40d481df4b6/image-61.jpg)







![[q, p] = i [H, q] = ω(–ip) [H, p] = ω(iq) From this [q, p] = i [H, q] = ω(–ip) [H, p] = ω(iq) From this](https://slidetodoc.com/presentation_image/3863ac9d5172e3e5026bb40d481df4b6/image-69.jpg)
![[H , F+] = – ωF+ HF+ – F+H = – ωF+ Operate on [H , F+] = – ωF+ HF+ – F+H = – ωF+ Operate on](https://slidetodoc.com/presentation_image/3863ac9d5172e3e5026bb40d481df4b6/image-70.jpg)








![[A , B] = 0 If A and B commute there exist eigenfunctions that [A , B] = 0 If A and B commute there exist eigenfunctions that](https://slidetodoc.com/presentation_image/3863ac9d5172e3e5026bb40d481df4b6/image-80.jpg)




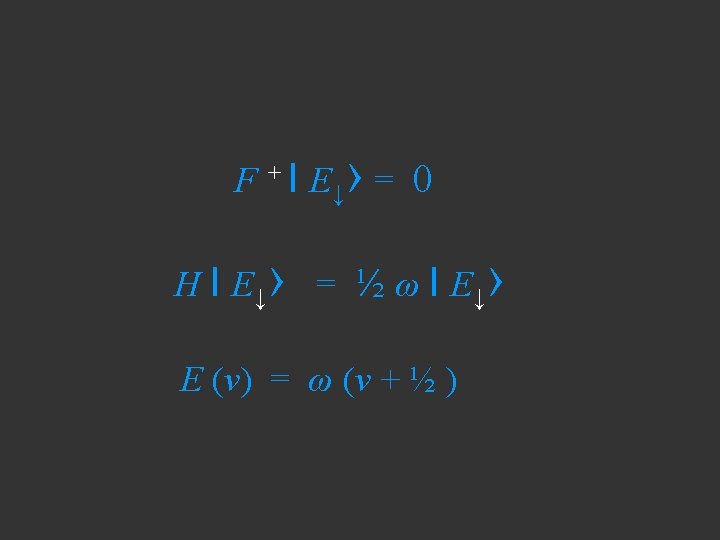

- Slides: 86

Let us discuss the harmonic oscillator

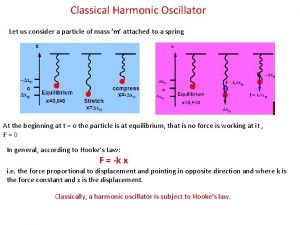
Let us discuss the harmonic oscillator E = T + V = ½mv 2 + ½kx 2

Let us discuss the harmonic oscillator E = T + V = ½mv 2 + ½kx 2 H = px 2/2 m + ½kx 2

Let us discuss the harmonic oscillator E = T + V = ½mv 2 + ½kx 2 H = px 2/2 m + ½kx 2 By a change of variables

Let us discuss the harmonic oscillator E = T + V = ½mv 2 + ½kx 2 H = px 2/2 m + ½kx 2 By a change of variables x = q(mω)-½ ω = (k/m)½

Let us discuss the harmonic oscillator E = T + V = ½mv 2 + ½kx 2 H = px 2/2 m + ½kx 2 By a change of variables x = q(mω)-½ ω = (k/m)½ We get a rather neater equation for the Hamiltonian

Let us discuss the harmonic oscillator E = T + V = ½mv 2 + ½kx 2 H = px 2/2 m + ½kx 2 By a change of variables x = q(mω)-½ ω = (k/m)½ We get a rather neater equation for the Hamiltonian H = ½ω(p 2 + q 2)


H = ½ω(p 2 + q 2) Let’s now consider this set of commutators

H = ½ω(p 2 + q 2) Let’s now consider this set of commutators NB that I have set ħ = 1 to simplify the relations

H = ½ω(p 2 + q 2) Let’s now consider this set of commutators NB that I have set ħ = 1 to simplify the relations [q, p] = i [H, q] = ω(-ip) [H, p] = ωiq

H = ½ω(p 2 + q 2) Let’s now consider this set of commutators NB that I have set ħ = 1 to simplify the relations [q, p] = i [H, q] = ω(-ip) [H, p] = ωiq From this set of quantum mechanical definitions

H = ½ω(p 2 + q 2) Let’s now consider this set of commutators NB that I have set ħ = 1 to simplify the relations [q, p] = i [H, q] = ω(-ip) [H, p] = ωiq From this set of quantum mechanical definitions We can invent a couple of B-type operators

H = ½ω(p 2 + q 2) Let’s now consider this set of commutators NB that I have set ħ = 1 to simplify the relations [q, p] = i [H, q] = ω(-ip) [H, p] = ωiq From this set of quantum mechanical definitions We can invent a couple of B-type operators ie operators that follow the form

H = ½ω(p 2 + q 2) Let’s now consider this set of commutators NB that I have set ħ = 1 to simplify the relations [q, p] = i [H, q] = ω(-ip) [H, p] = ωiq From this set of quantum mechanical definitions We can invent a couple of B-type operators ie operators that follow the form AB – BA = k. B

AB – BA = k. B







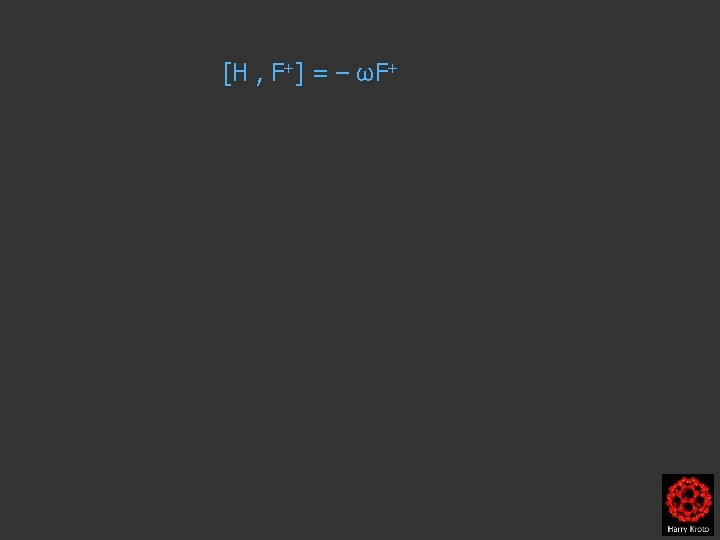

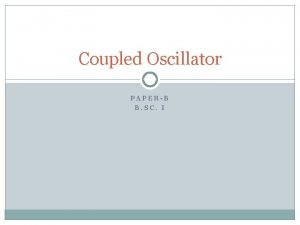
![H F ωF HF FH ωF Now lets [H , F+] = – ωF+ HF+ – F+H = – ωF+ Now let’s](https://slidetodoc.com/presentation_image/3863ac9d5172e3e5026bb40d481df4b6/image-26.jpg)
[H , F+] = – ωF+ HF+ – F+H = – ωF+ Now let’s operate with both sides of this expression on a particular eigenfunction En
![H F ωF HF FH ωF Now lets [H , F+] = – ωF+ HF+ – F+H = – ωF+ Now let’s](https://slidetodoc.com/presentation_image/3863ac9d5172e3e5026bb40d481df4b6/image-27.jpg)
[H , F+] = – ωF+ HF+ – F+H = – ωF+ Now let’s operate with both sides of this expression on a particular eigenfunction En ie the nth eigenfunction defined by
![H F ωF HF FH ωF Now lets [H , F+] = – ωF+ HF+ – F+H = – ωF+ Now let’s](https://slidetodoc.com/presentation_image/3863ac9d5172e3e5026bb40d481df4b6/image-28.jpg)
[H , F+] = – ωF+ HF+ – F+H = – ωF+ Now let’s operate with both sides of this expression on a particular eigenfunction En ie the nth eigenfunction defined by H En = En En
![H F ωF HF FH ωF Now lets [H , F+] = – ωF+ HF+ – F+H = – ωF+ Now let’s](https://slidetodoc.com/presentation_image/3863ac9d5172e3e5026bb40d481df4b6/image-29.jpg)
[H , F+] = – ωF+ HF+ – F+H = – ωF+ Now let’s operate with both sides of this expression on a particular eigenfunction En ie the nth eigenfunction defined by H En = En En H F+ En – F+H En = – ωF+ En
![H F ωF HF FH ωF Now lets [H , F+] = – ωF+ HF+ – F+H = – ωF+ Now let’s](https://slidetodoc.com/presentation_image/3863ac9d5172e3e5026bb40d481df4b6/image-30.jpg)
[H , F+] = – ωF+ HF+ – F+H = – ωF+ Now let’s operate with both sides of this expression on a particular eigenfunction En ie the nth eigenfunction defined by H En = En En H F+ En – F+H En = – ωF+ En H F+ En – En. F+ En = – ωF+ En
![H F ωF HF FH ωF Now lets [H , F+] = – ωF+ HF+ – F+H = – ωF+ Now let’s](https://slidetodoc.com/presentation_image/3863ac9d5172e3e5026bb40d481df4b6/image-31.jpg)
[H , F+] = – ωF+ HF+ – F+H = – ωF+ Now let’s operate with both sides of this expression on a particular eigenfunction En ie the nth eigenfunction defined by H En = En En H F+ En – F+H En = – ωF+ En H F+ En – En. F+ En = – ωF+ En H F+ En = (En – ω) F+ En
![H F ωF HF FH ωF Now lets [H , F+] = – ωF+ HF+ – F+H = – ωF+ Now let’s](https://slidetodoc.com/presentation_image/3863ac9d5172e3e5026bb40d481df4b6/image-32.jpg)
[H , F+] = – ωF+ HF+ – F+H = – ωF+ Now let’s operate with both sides of this expression on a particular eigenfunction En ie the nth eigenfunction defined by H En = En En H F+ En – F+H En = – ωF+ En H F+ En – En. F+ En = – ωF+ En H F+ En = (En – ω) F+ En So F+ has operated on En to produce a new eigenfunction with eigenvalue En – ω

En



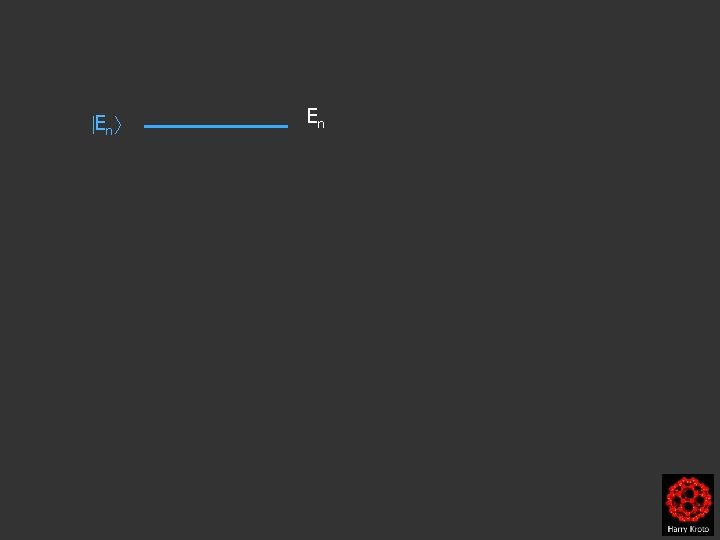
En En – ω En – 2ω Let’s ladder down till we get to the last eigenvalue at which a next application of F+ would produce an eigenstate with negative energy which we shall posutlate is not allowed and so F+ must annihilate this last eigenstate ie F+ E↓ = 0

En En – ω En – 2ω F+ E↓ Aaaaghhhhh…… E↓ Let’s ladder down till we get to the last eigenvalue at which a next application of F+ would produce an eigenstate with negative energy which we shall posutlate is not allowed and so F+ must annihilate this last eigenstate ie F+ E↓ = 0


F+F– = (q + ip)(q – ip) = q 2 – iqp + ipq +p 2

F+F– = (q + ip)(q – ip) = q 2 – iqp + ipq +p 2 = q 2 – i[q, p] + p 2

F+F– = (q + ip)(q – ip) = q 2 – iqp + ipq +p 2 = q 2 – i[q, p] + p 2 = q 2 + p 2 + 1











They are F± = q ± ip By inspection we can show that [H , F+] = – ωF+ [H , F–] = + ωF– These are of the form [A , B] = k. B So the Fs are B-type operators

Now H can be factorised as H = ½ω(F+F– – 1) H = ½ω(F– F+ + 1) H = ½ω(F+ F– – 1) H = ½ω(F– F+ + 1)

Now H can be factorised as H = ½ω(F+F– – 1) H = ½ω(F– F+ + 1) H{F+ En } = (En – ω){F+ En } H{F– En } = (En– ω){F– En }

Now H can be factorised as H F+ En = ½ω(F+F– – 1) F+ En H{F+ En } = (En – ω){F+ En } H{F– En } = (En– ω){F– En }


Let us discuss the harmonic oscillator E = T + V = ½m 2 + ½kx 2 H = p 2/2 m + ½kx 2 By a change of variables x = q(mω)-½ ω = (k/m)½ We get a rather neater equation for the Hamiltonian H = ½ω(p 2 + q 2)

Let us discuss the harmonic oscillator E = T + V = ½m 2 + ½kx 2 H = p 2/2 m + ½kx 2 By a change of variables x = q(mω)-½ ω = (k/m)½ We get a rather neater equation for the Hamiltonian H = ½ω(p 2 + q 2)

H = ½ω(p 2 + q 2) Let’s now consider this set of commutators NB that I have set ħ = 1 to simplify the relations [q, p] = i [H, q] = ω(-ip) [H, p] = ωiq From this set of quantum mechanical definitions We can invent a couple of B-type operators ie one that follows the form AB – BA = ±k. B
![q p i H q ωip H p ωiq From this [q, p] = i [H, q] = ω(–ip) [H, p] = ω(iq) From this](https://slidetodoc.com/presentation_image/3863ac9d5172e3e5026bb40d481df4b6/image-60.jpg)
[q, p] = i [H, q] = ω(–ip) [H, p] = ω(iq) From this set of quantum mechanical definitions We can invent a couple of B-type operators ie one that follows the form AB – BA = ±k. B F+ = q + ip [H, F+] = [H, q] + i[H, p] = ω(–ip) + iω(iq) = ω(–ip – q) = – ωF+ [H, F+] = –ωF+ and [H , F–] = +ωF–
![H F ωF HF FH ωF Operate on [H , F+] = – ωF+ HF+ – F+H = – ωF+ Operate on](https://slidetodoc.com/presentation_image/3863ac9d5172e3e5026bb40d481df4b6/image-61.jpg)
[H , F+] = – ωF+ HF+ – F+H = – ωF+ Operate on a particular eigenfunction En ie the nth eigenfunction defined by H En = En En with both sides H F+ En – F+H En = – ωF+ En H F+ En – En. F+ En = – ωF+ En H F+ En = (En – ω) F+ En

They are F± = q ± ip By inspection we can show that [H , F+] = – ωF+ [H , F–] = + ωF– These are of the form [A , B] = k. B So the Fs are B-type operators

Now H can be factorised as H = ½ω(F+F– – 1) H = ½ω(F– F+ + 1) H = ½ω(F+ F– – 1) H = ½ω(F– F+ + 1)

Now H can be factorised as H = ½ω(F+F– – 1) H = ½ω(F– F+ + 1) H{F+ En } = (En – ω){F+ En } H{F– En } = (En– ω){F– En }

Now H can be factorised as H F+ En = ½ω(F+F– – 1) F+ En H{F+ En } = (En – ω){F+ En } H{F– En } = (En– ω){F– En }



H = ½ω(p 2 + q 2) Let’s now consider this set of commutators NB that I have set ħ = 1 to simplify the relations [q, p] = i [H, q] = ω(-ip) [H, p] = ωiq From this set of quantum mechanical definitions We can invent a couple of B-type operators ie one that follows the form AB – BA = ±k. B
![q p i H q ωip H p ωiq From this [q, p] = i [H, q] = ω(–ip) [H, p] = ω(iq) From this](https://slidetodoc.com/presentation_image/3863ac9d5172e3e5026bb40d481df4b6/image-69.jpg)
[q, p] = i [H, q] = ω(–ip) [H, p] = ω(iq) From this set of quantum mechanical definitions We can invent a couple of B-type operators ie one that follows the form AB – BA = ±k. B F+ = q + ip [H, F+] = [H, q] + i[H, p] = ω(–ip) + iω(iq) = ω(–ip – q) = – ωF+ [H, F+] = –ωF+ and [H , F–] = +ωF–
![H F ωF HF FH ωF Operate on [H , F+] = – ωF+ HF+ – F+H = – ωF+ Operate on](https://slidetodoc.com/presentation_image/3863ac9d5172e3e5026bb40d481df4b6/image-70.jpg)
[H , F+] = – ωF+ HF+ – F+H = – ωF+ Operate on a particular eigenfunction En ie the nth eigenfunction defined by H En = En En with both sides H F+ En – F+H En = – ωF+ En H F+ En – En. F+ En = – ωF+ En H F+ En = (En – ω) F+ En

n En En – ω En – 2ω Let’s ladder down till we get to the last eigenvalue at which a next application of F+ would produce an eigenstate with negative energy which we shall posutlate is not allowed and that must annihilate this last eigenstate ie F+ E↓ = 0 F+ Aaaaghhhhh…… E↓


They are F± = q ± ip By inspection we can show that [H , F+] = – ωF+ [H , F–] = + ωF– These are of the form [A , B] = k. B So the Fs are B-type operators

Now H can be factorised as H = ½ω(F+F– – 1) H = ½ω(F– F+ + 1) H = ½ω(F+ F– – 1) H = ½ω(F– F+ + 1)

Now H can be factorised as H = ½ω(F+F– – 1) H = ½ω(F– F+ + 1) H{F+ En } = (En – ω){F+ En } H{F– En } = (En– ω){F– En }

Now H can be factorised as H F+ En = ½ω(F+F– – 1) F+ En H{F+ En } = (En – ω){F+ En } H{F– En } = (En– ω){F– En }



![A B 0 If A and B commute there exist eigenfunctions that [A , B] = 0 If A and B commute there exist eigenfunctions that](https://slidetodoc.com/presentation_image/3863ac9d5172e3e5026bb40d481df4b6/image-80.jpg)
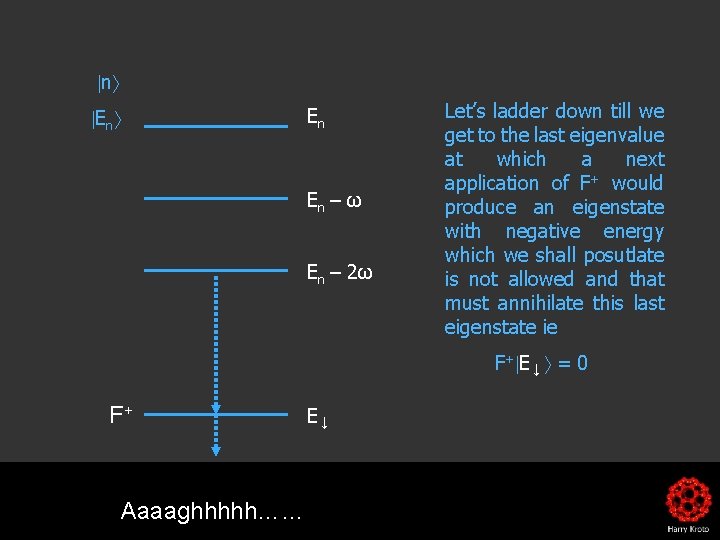
[A , B] = 0 If A and B commute there exist eigenfunctions that are simultaneously eigenfunctions of both operators A and B and one can determine simultaneously the values of the quantities represented by the two operators but if they do not commute one cannot determine the values of the quantities simultaneously




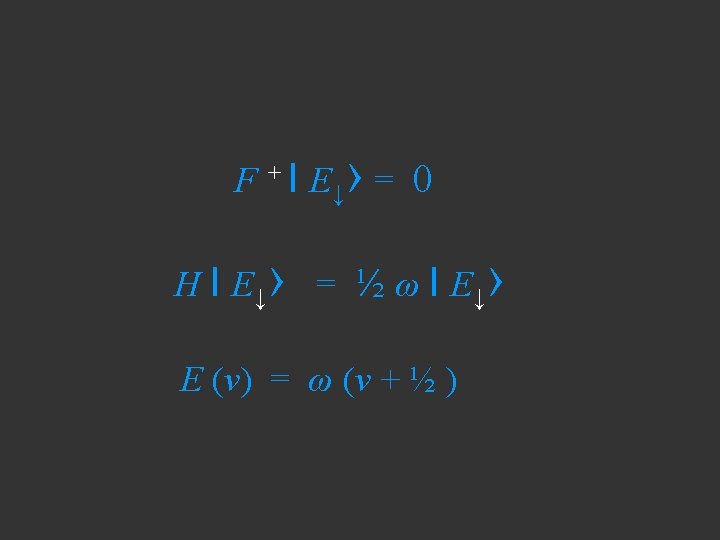

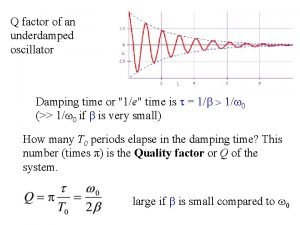
 Relaxation time of damped harmonic oscillator
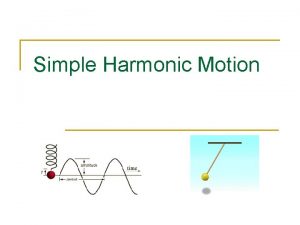
Relaxation time of damped harmonic oscillator Simple harmonic oscillator
Simple harmonic oscillator Morse potential
Morse potential Frequency of oscillation
Frequency of oscillation Simple harmonic oscillator amplitude
Simple harmonic oscillator amplitude Mechanical energy
Mechanical energy Hooke's law simple definition
Hooke's law simple definition Selection rule for simple harmonic oscillator
Selection rule for simple harmonic oscillator Harmonic oscillator propagator
Harmonic oscillator propagator Harmonic oscillator selection rules
Harmonic oscillator selection rules Harmonic oscillator spring
Harmonic oscillator spring Q factor damped harmonic oscillator
Q factor damped harmonic oscillator 戴明鳳
戴明鳳 Energy of harmonic oscillator
Energy of harmonic oscillator Harmonic oscillator
Harmonic oscillator Tension wave
Tension wave Let me let me let me
Let me let me let me Amateurs discuss tactics professionals discuss logistics
Amateurs discuss tactics professionals discuss logistics Let discuss what wearing
Let discuss what wearing Lets think in english
Lets think in english Let's discuss the story so far
Let's discuss the story so far An oscillator converts
An oscillator converts Oscillator definition
Oscillator definition In a voltage shunt feedback circuit,
In a voltage shunt feedback circuit, Lc oscillator simulation
Lc oscillator simulation Barkhausen criteria of oscillator
Barkhausen criteria of oscillator Application of programmable unijunction transistor
Application of programmable unijunction transistor An oscillator converts …………….. *
An oscillator converts …………….. * Lc oscillator
Lc oscillator Need of oscillator
Need of oscillator Lc feedback oscillator
Lc feedback oscillator Types of oscillator
Types of oscillator Relaxation oscillator schmitt trigger
Relaxation oscillator schmitt trigger Voltage controlled oscillator
Voltage controlled oscillator Minecraft 102
Minecraft 102 Colpitts oscillator frequency formula
Colpitts oscillator frequency formula L c oscillator
L c oscillator Op amp oscillator
Op amp oscillator Mti radar with power amplifier transmitter
Mti radar with power amplifier transmitter Oscillator analog electronics
Oscillator analog electronics What is audio oscillator
What is audio oscillator Half center oscillator
Half center oscillator Series fed hartley oscillator
Series fed hartley oscillator Oscillator phase noise 50low
Oscillator phase noise 50low Barkhausen criteria of oscillator
Barkhausen criteria of oscillator Osilator amstrong
Osilator amstrong Trigger
Trigger Barkhausen criteria of oscillator
Barkhausen criteria of oscillator Ujt relaxation oscillator
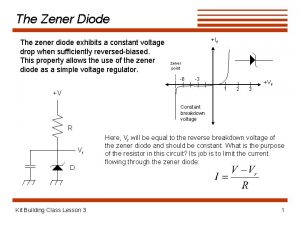
Ujt relaxation oscillator Zener diodes exhibit
Zener diodes exhibit Malha
Malha Properties of ultrasonic waves
Properties of ultrasonic waves Cmos lc oscillator
Cmos lc oscillator Phase shift oscillator
Phase shift oscillator He who has ears to hear let him hear revelation
He who has ears to hear let him hear revelation Indirect object answers the question
Indirect object answers the question What did you say
What did you say Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Từ ngữ thể hiện lòng nhân hậu
Từ ngữ thể hiện lòng nhân hậu Tư thế ngồi viết
Tư thế ngồi viết Diễn thế sinh thái là
Diễn thế sinh thái là V. c c
V. c c 101012 bằng
101012 bằng Hát lên người ơi alleluia
Hát lên người ơi alleluia Khi nào hổ mẹ dạy hổ con săn mồi
Khi nào hổ mẹ dạy hổ con săn mồi đại từ thay thế
đại từ thay thế Vẽ hình chiếu vuông góc của vật thể sau
Vẽ hình chiếu vuông góc của vật thể sau Quá trình desamine hóa có thể tạo ra
Quá trình desamine hóa có thể tạo ra Cong thức tính động năng
Cong thức tính động năng Thế nào là mạng điện lắp đặt kiểu nổi
Thế nào là mạng điện lắp đặt kiểu nổi Hát kết hợp bộ gõ cơ thể
Hát kết hợp bộ gõ cơ thể Tỉ lệ cơ thể trẻ em
Tỉ lệ cơ thể trẻ em Lời thề hippocrates
Lời thề hippocrates Dạng đột biến một nhiễm là
Dạng đột biến một nhiễm là Vẽ hình chiếu đứng bằng cạnh của vật thể
Vẽ hình chiếu đứng bằng cạnh của vật thể độ dài liên kết
độ dài liên kết Môn thể thao bắt đầu bằng từ đua
Môn thể thao bắt đầu bằng từ đua Khi nào hổ mẹ dạy hổ con săn mồi
Khi nào hổ mẹ dạy hổ con săn mồi điện thế nghỉ
điện thế nghỉ Biện pháp chống mỏi cơ
Biện pháp chống mỏi cơ Trời xanh đây là của chúng ta thể thơ
Trời xanh đây là của chúng ta thể thơ Gấu đi như thế nào
Gấu đi như thế nào Lp html
Lp html Thiếu nhi thế giới liên hoan
Thiếu nhi thế giới liên hoan Số nguyên tố là
Số nguyên tố là Phối cảnh
Phối cảnh Một số thể thơ truyền thống
Một số thể thơ truyền thống