Lesson Objectives Aims Understand the following 1 The

Lesson Objectives Aims Understand the following: 1. The big O notation

Big O Notation • Big O is the “Order” of magnitude for an algorithm • What does that mean? • It’s an estimate of the time an algorithm will take for a given data set. • It can be used to measure its efficiency

Big O • Represented as O(function of N) • N = the size of the input data set • O = generally the worst case scenario

Big O • Algorithms, and indeed algorithmic complexity, are divided in to types: • • • Constant Linear Polynomial Exponential Logarithmic

Key Points • Big O notation is used to show: – The time algorithms take – Or the space they need – increases as the size of the data set they operate on increases

Calculating big O • We can express the complexity of an algorithm in an equation • We then simplify the equation to express the term in one of the big O forms (linear, exponential etc)

Example • 7 n 3 + n 2 + 4 n +1 • as n increases - what happens to the different terms of this equation? • The larger n gets, the less an impact n 2 + 4 n +1 has on the total compared to n 3

• To calculate Big O for a given expression: – Remove all terms except the one with the largest exponent – Remove any constant factors

Questions

• 1 = O(n 4) = Polynomial • 2 = O(n) = linear complexity

Questions

• 3 = O(n 2) = Quadratic • 4 = O(10) = Constant

Constant complexity O(1) • O(1) Algorithms take the same time to run regardless of the size of the dataset • Example: push an item to the stack

Linear complexity O(n) • The time taken to solve an O(n) algorithms increases at the same rate as the input size • If the input dataset doubles in size, the time taken doubles • Example: find an element using linear search

Polynomial complexity • O(nk) where k is a positive integer • The complexity varies depending on the power of the function. – If k = 0: n^0 = 1 constant complexity – If k = 1 linear complexity – If K = 2 quadratic complexity – If K = 3 cubic complexity
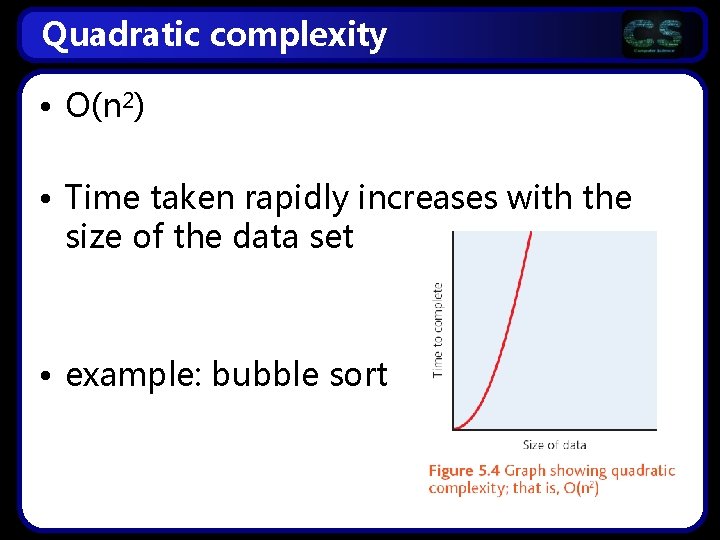
Quadratic complexity • O(n 2) • Time taken rapidly increases with the size of the data set • example: bubble sort

Exponential complexity • Instead of O(nk), it is O(kn) • Time taken rises at a much faster rate than polynomial complexity • The complexity is to the power of the number of elements • Does not scale well

Logarithmic Complexity • O(log n) • Start off expensive • As the data set grows, the complexity decreases and eventually levels out • A good situation to be in • E. g. Binary Search.
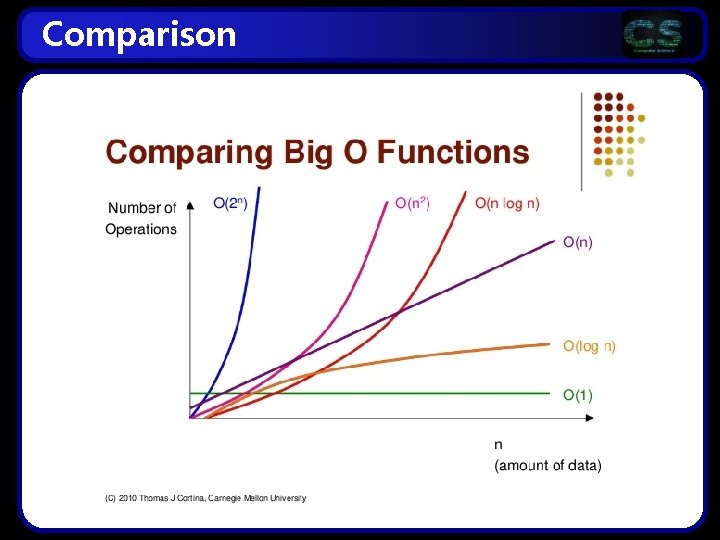
Comparison

Reading • https: //rob-bell. net/2009/06/abeginners-guide-to-big-o-notation/ • https: //justin. abrah. ms/computerscience/big-o-notation-explained. html • Shows in the context of code
Review/Success Criteria You should know: ü The
- Slides: 21