Lesson Objectives Aims A Be able to identify

Lesson Objectives Aims A. Be able to identify and use primitive data types such as Integer, real, character, string and Boolean B. Represent positive integers in binary C. Use sign and magnitude or twos compliment to represent negative binary numbers D. Be able to perform addition and subtraction in binary (integers) E. Represent positive integers as Hexadecimal F. Convert integers between Binary, Hex and Denary

Primitive data types • If you don’t know these by now you: – Haven’t done your homework – Haven’t been completing programming tasks – Can’t program…

• Create a table with the following headings and fill it in, without using the internet or a book: Data Type Integer Real/Float Character String Boolean Description Example

Binary Quantities • The smallest piece of information a computer can understand is a 1 or a 0 • This single digit is called a BIT. • Obviously, this isn’t too useful on its own. • If we group 4 BITS together, we have 16 possible combinations – a NYBBLE

• • 1 or 0 = Bit 4 bits = Nybble 8 bits = Byte (most common grouping) 1024 bits = 1 Kilobyte (Kb) (2^10) 1024 Kb = 1 Megabyte (Mb) (2^20) 1024 Mb = 1 Gigabyte (Gb) (2^30) 1024 Gb = 1 Terabyte (Tb) (2^40) 1024 Tb = 1 Petabyte (Pb) (2^50) All are powers of 2

Denary • We count in a number system called Denary • It is a BASE 10 number system because… • There are 10 digits! • 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 (if you were wondering)

Number systems • Think about what happens when we count… • Eventually we run out of digits • What happens at 9? • What REALLY does this mean? • What does it tell you about the PLACE each number has?

Number systems • What does the Denary number 1654 mean? Thousands (x 1000) Hundreds (x 100) Tens (x 10) Units (x 1) 1 6 5 4 1654 = 1 x 1000 + 6 x 100 + 5 x 10 + 4 x 1

• So now we should understand the following ideas: – The BASE of our number system is given by the number of digits we have available – The PLACE of a digit denotes its value – The place value is determined by multiplying the previous column value by the base of the number system It’s all about the BASE. Geddit? See what I did there?

Number systems used in CS Number system Base Binary 2 Octal 8 Denary 10 Hexadecimal 16

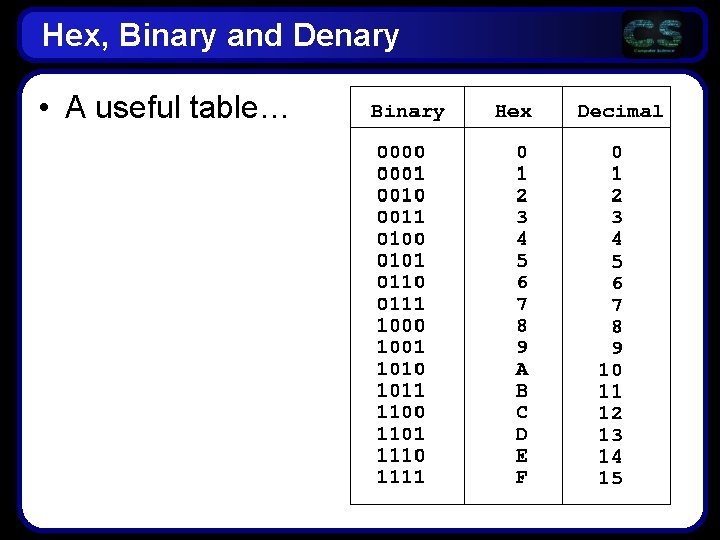
Hex, Binary and Denary • A useful table…

Binary 128 64 32 16 8 4 2 1 1 0 0 0 1 1 • Binary has only 2 digits • Which is why we have the place/column values shown above • If we take a Byte of data, we can store numbers up to 255 • Or 256 different COMBINATIONS of numbers (including zero)

Hexadecimal • Binary numbers can quickly become long and cumbersome • This makes them difficult for us to understand • Think about how easy it would be to make an error copying a number such as 1101010110001110000111100101

• Hexadecimal allows us to shorten these numbers significantly. • Hexadecimal is base 16 • There are 16 digits: • 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F

• Each column is now worth 16 x the previous: 4096 256 16 1 1 5 F 8 • = 4096*1 + 256*5 + 16*15 + 1*8 • = 4096 + 1280 + 240 + 8 • = 5624

Denary (Decimal) to binary • Convert 187 to Binary 128 64 32 16 8 4 2 1 1. Write out your table (just keep doubling each number from 1) 2. Working from LEFT to RIGHT, put a 1 under each number that is nearest to your remaining total 3. 4. 5. 6. 7. 8. 9. 187 – 128 = 59 59 – 32 = 27 27 – 16 = 11 11 – 8 = 3 3– 2=1 1 -1 = 0 187 = 1011

Denary (Decimal) to Hex • First convert to Binary • 187 = 1011 128 64 32 16 8 4 2 1 1 0 1 1 • • • Then split in to two Nybbles 1011 Convert Nybbles to Hex 1011 = B in Hex 187 = BB

Hex to Binary • Take each hex digit • F 8 • Turn each in to a 4 bit Nybble • F = 1111, 8 = 1000 • Combine: • 11111000

Hex to Decimal (Denary) • Convert to Binary first! • Then convert from Binary to Decimal • F 8 = 11111000 • 11111000 = 128 + 64 + 32 + 16 + 8 • = 248

Addition and Subtraction • Addition is eeeeeaasssssyyyyy • Repeat after me: Sum Equals 0+0 0 0+1 1 1+0 1 1+1 0… er? • Which truth table is this…?

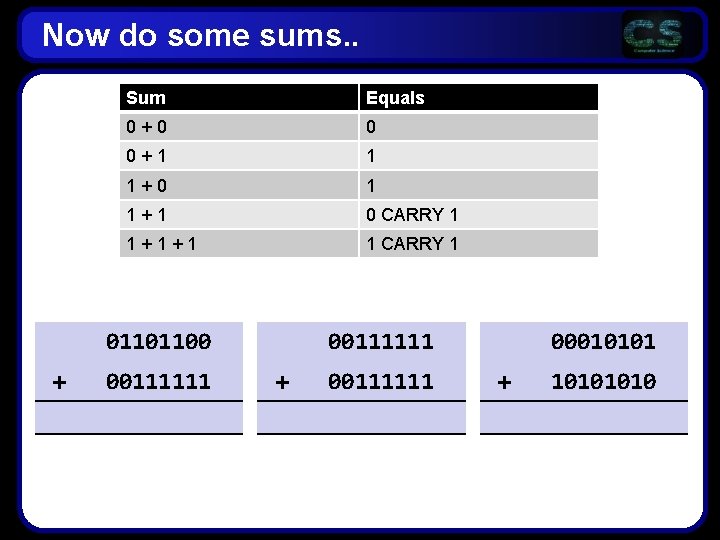
Now do some sums. . Sum Equals 0+0 0 0+1 1 1+0 1 1+1 0 CARRY 1 1+1+1 1 CARRY 1 00111111 01101100 + 00111111 00010101 + 1010

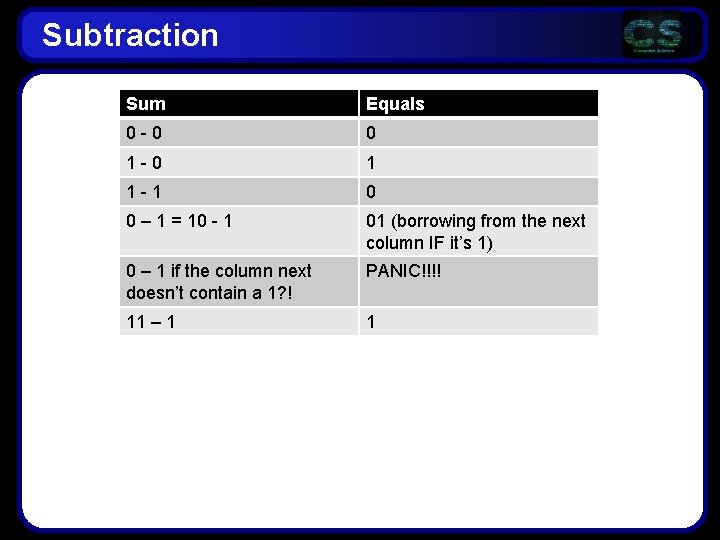
Subtraction Sum Equals 0 -0 0 1 -0 1 1 -1 0 0 – 1 = 10 - 1 01 (borrowing from the next column IF it’s 1) 0 – 1 if the column next doesn’t contain a 1? ! PANIC!!!! 11 – 1 1

Worked Examples 1011 - 0011 1– 1=0 0– 0=0 1– 0=1 Answer - 1000

10 - 5 1010 - 1010 0101 ---01 0101 1010 0101 ---0101

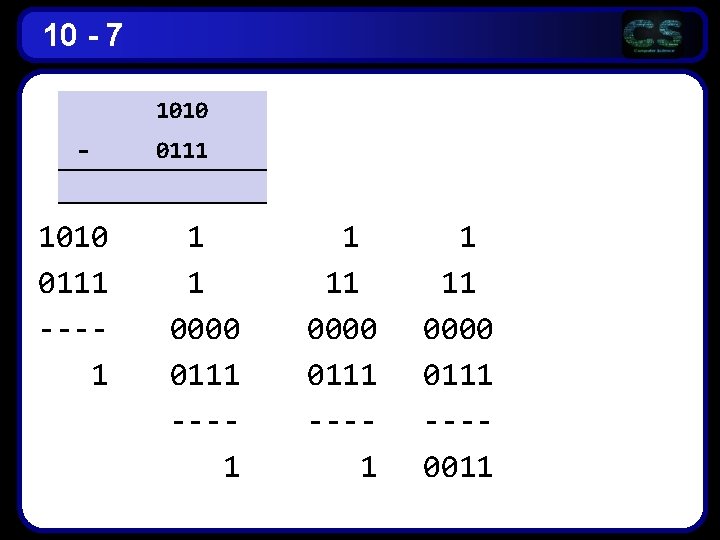
10 - 7 1010 - 1010 0111 ---1 0111 1 1 0000 0111 ---1 1 11 0000 0111 ---0011

00111011 1111 - 00001111 - 01000000 0010 - 00101011 - 00001111

• But… what about negative numbers? ? • There has to be a way? • Yes, but it’s a compromise which reduces the maximum size of a number that can be stored in a byte.

Sign and magnitude • The simplest system is sign and magnitude • Normal binary number (150): 128 64 32 16 8 4 2 1 1 0 0 1 1 0 • Sign and magnitude (-22) Sign 1 Magnitude 64 32 16 8 4 2 1 0 0 1 1 0

• Sign bit = 0 or 1 § 1 = negative § 0 = positive • Magnitude = the size of the actual number

Two’s Compliment • Sets the sign bit to be negative (like in sign and magnitude) • But it’s not a flag – it means the negative value of its column • So in 8 bit numbers, -128

Two’s compliment conversion To represent the number -13 as an 8 -bit binary number. . . Step 1 : Convert the positive number 13 into an 8 -bit binary integer: 128 64 32 16 8 4 2 1 0 0 1 1 0 1 Step 2 : Change all the bits from 0 to 1 (or from 1 to 0. ) 128 64 32 16 8 4 2 1 0 1 0 1 1 0 Step 3 : Add 1 - Perform a binary calculation. 1 0 1 0 0 0 1 0 1 1 +

• The column values are now slightly different. • What negative number is this? - 128 64 32 16 8 4 2 1 1 0 1 1 • Flip the bits and add 1! • Or -128+32+16+8+2+1

Subtraction with 2’s compliment 10 – 4… 10 = 00001010 4 = 00000100 Convert the number to subtract (4) in to two’s compliment: 11111100 Now add… 00001010 11111100 -------100000110 The 1 has overflowed (consider it dead…) what’s left is the correct answer.

Lesson Objectives Aims I. Perform bitwise manipulation and use masks with AND, OR and XOR J. Understand the use of character sets (ASCII and Unicode) to represent text Key Words

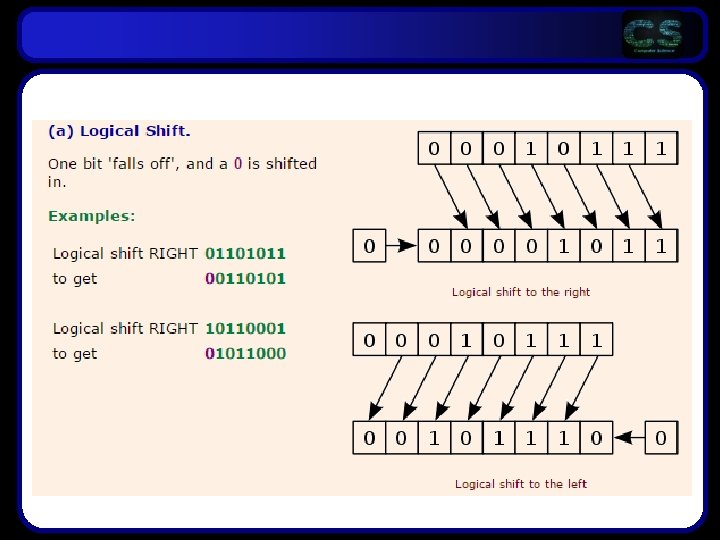
Logical Operators • Processors will have the ability to perform “shift” operations • There are two types: – Logical – Arithmetic • They both have similar effects but are subtly different

• Why - Quick arithmetic! • Shifting bits RIGHT will DIVIDE the number by 2 • Shifting bits LEFT will MULTIPLY the number by 2

Operators • You MUST be already familiar with: 1. 2. 3. 4. NOT AND OR XOR

• • Not – inverse, 1’s compliment AND – Find the status of a bit OR – Reset/Change values XOR – find matching bits • Any byte/register size operations with these are called “masks” or “bitwise manipulation” • E. g. AND 00011001 00000001 (mask) 00000001

ASCII and Unicode • ASCII – 127 characters (8 bits, 1 parity) • Unicode – 16 bits, now more – Enables all languages to be stored – World wide standard – Should display on any device/OS/Compliant software

Review/Success Criteria