Lesson Derivative Basics 1 v Obj Tangent Lines

Lesson: Derivative Basics 1 v Obj- Tangent Lines and rates of change.

v What do you know about the following? 1. 2. 3.

v Congratulations! You now know what a derivative is. A derivative can be thought of as a slope or a rate of change. It’s simply a measure of how much one thing changes, compared to another. Examples: mi/hr, ft/sec, students/class, etc…

1. Derivative – The slope of the tangent line of a curve. - Instantaneous rate of change - y’, f ’(x), dy/dx, d/dx

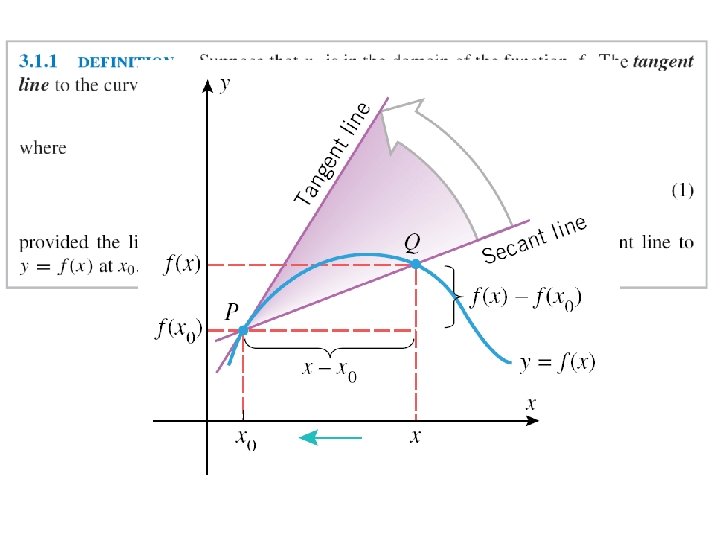
Recall: The derivative is just a slope. Therefore, the formula above can also be used to find the slope of the tangent line. (It is called the “Difference Quotient”)

EX. 1: Use the definition of the derivative to: A. Find the slope of the tangent line of the curve f(x) = x 2 at the point (1, 1) B. Find the equation of the tangent line mentioned above.

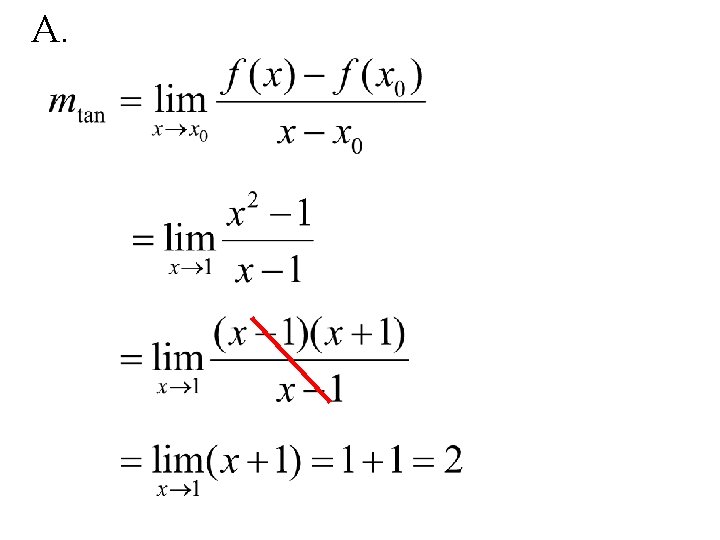
A.

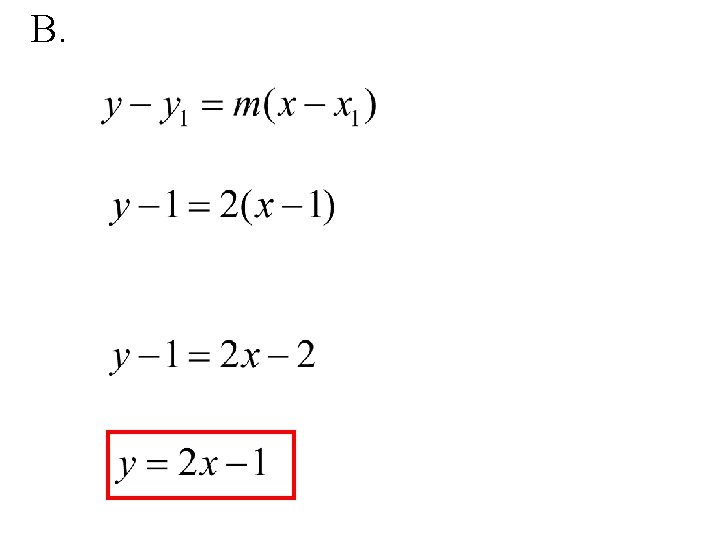
B.

EX. 2: A. Find the slope of the tangent line of the curve f(x) = x 2 at the point (-4, 16) B. Find the equation of the tangent line mentioned above.

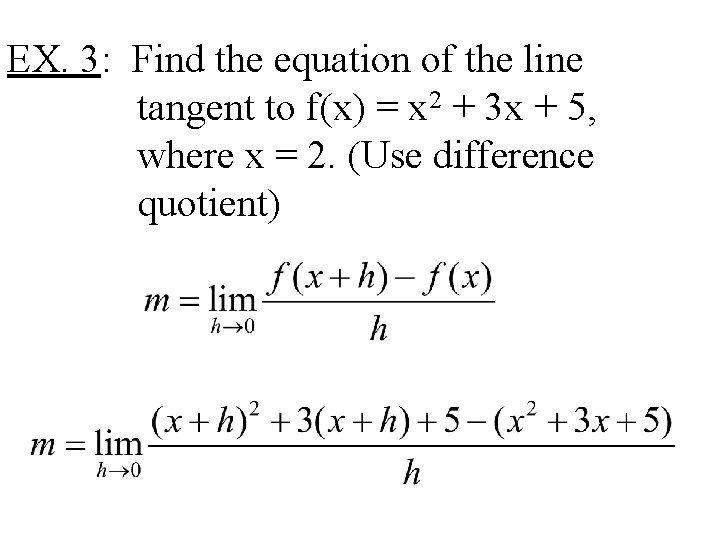
EX. 3: Find the equation of the line tangent to f(x) = x 2 + 3 x + 5, where x = 2. (Use difference quotient)

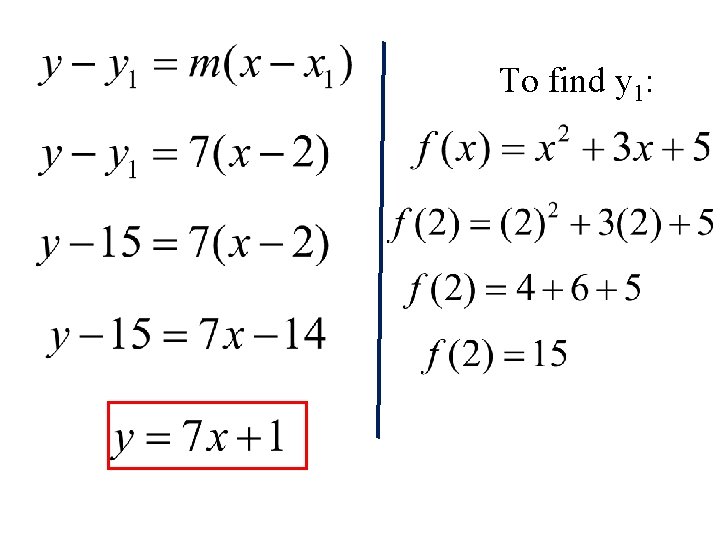
To find y 1:

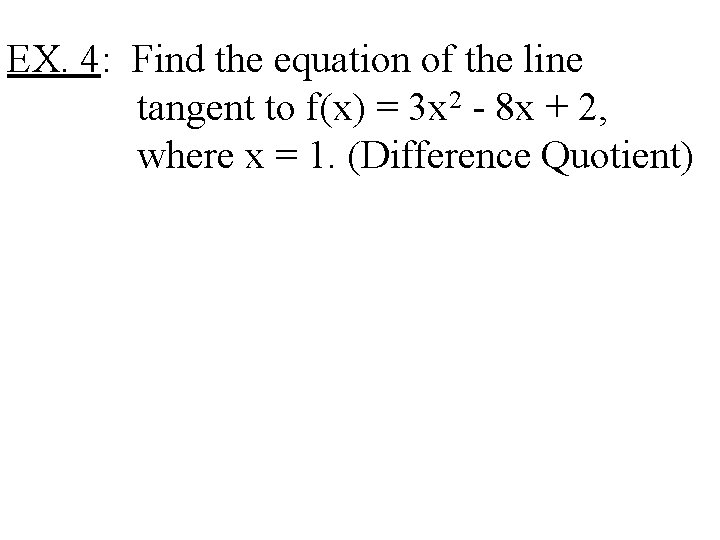
EX. 4: Find the equation of the line tangent to f(x) = 3 x 2 - 8 x + 2, where x = 1. (Difference Quotient)

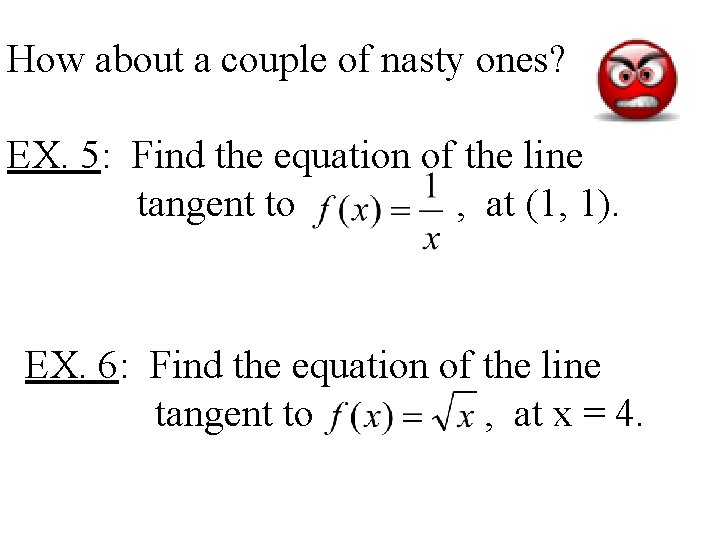
How about a couple of nasty ones? EX. 5: Find the equation of the line tangent to , at (1, 1). EX. 6: Find the equation of the line tangent to , at x = 4.

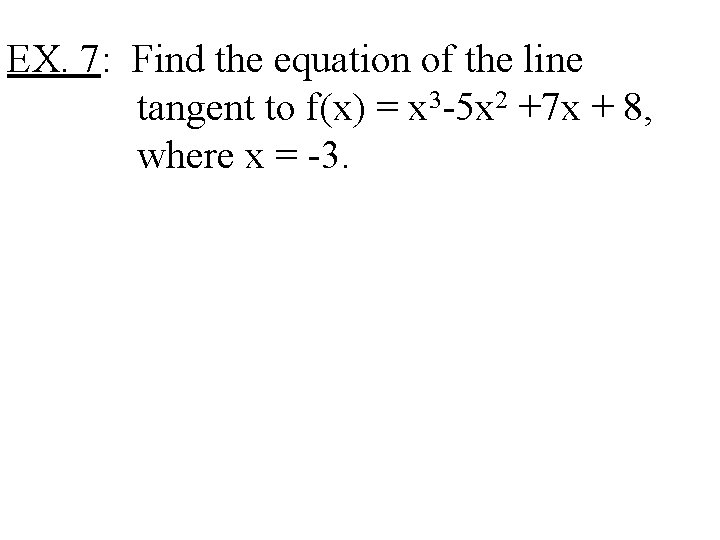
EX. 7: Find the equation of the line tangent to f(x) = x 3 -5 x 2 +7 x + 8, where x = -3.

Ex. 8: Let y = x 2 + 1 A. Find the “average rate of change” of y, with respect to x, over the interval [3, 5]. B. Find the “instantaneous rate of change” of y, with respect to x, when x = -4.

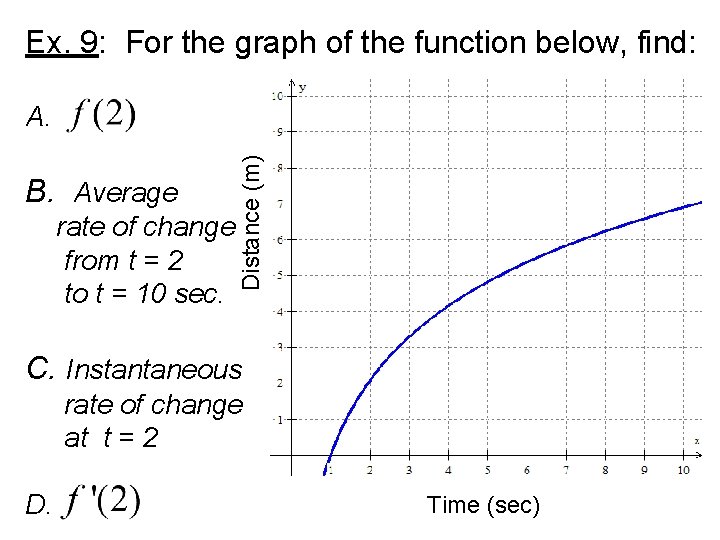
Ex. 9: For the graph of the function below, find: B. Average rate of change from t = 2 to t = 10 sec. Distance (m) A. C. Instantaneous rate of change at t = 2 D. Time (sec)