Lesson 9 5 Objective To solve quadratic equations

Lesson 9. 5 Objective: To solve quadratic equations using the quadratic formula. What formula can be used to solve any quadratic equation? Quadratic formula: When Then the value of x is…

Example: Use the quadratic equation to solve for x. a=1 b=9 c = 14

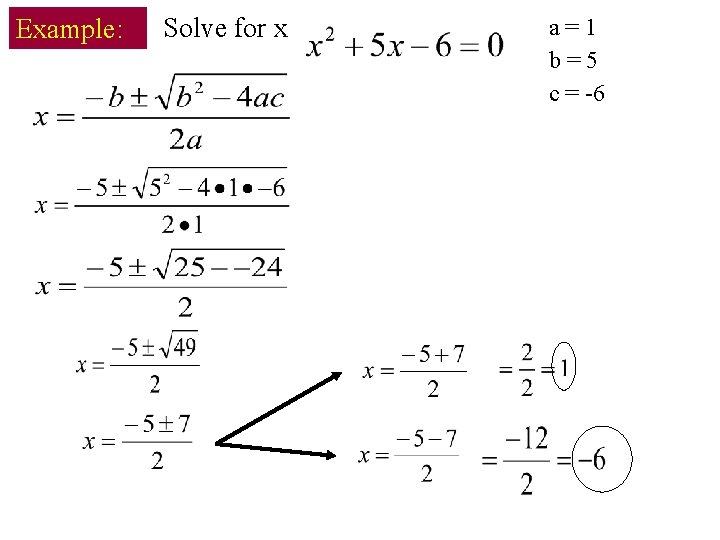
Example: Solve for x a=1 b=5 c = -6

Example: a = -2 b=6 c=9 Solve for x Simplify Simplified

Vertical Motion Model A ball is thrown upwards with an initial velocity of 90 feet per second from a height of 6 feet. Use the vertical motion model to determine the time it will take the ball to hit the ground. a = -16 b = 90 c = 6 h = height of ground t = time v = initial velocity s = starting height

Applications of the Discriminant The discriminant is the expression inside the radical in the quadratic formula, b 2 – 4 ac. • If b 2 – 4 ac is positive, then the equation has two solutions. • If b 2 – 4 ac is zero, then the equation has one solution. • If b 2 – 4 ac is negative, then the equation has no real solution.

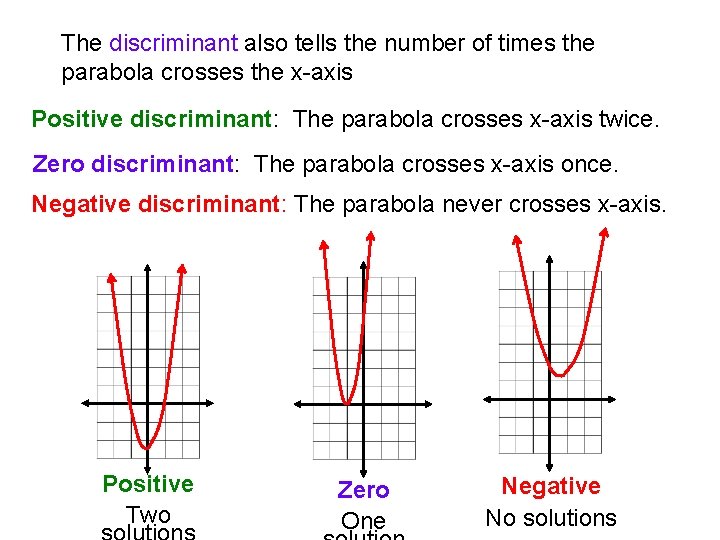
The discriminant also tells the number of times the parabola crosses the x-axis Positive discriminant: The parabola crosses x-axis twice. Zero discriminant: The parabola crosses x-axis once. Negative discriminant: The parabola never crosses x-axis. Positive Two Zero One Negative No solutions

Examples: Find the discriminant and determine the number of solutions 1. a =1 b =-3 c =-4 9 - -16 25 Two solutions 2. a =1 b =2 c =5 4 – 20 – 16 No solutions 3. 16 – 16 0 One solution