Lesson 9 3 Hyperbolas Hyperbola Set of all

Lesson 9. 3 Hyperbolas

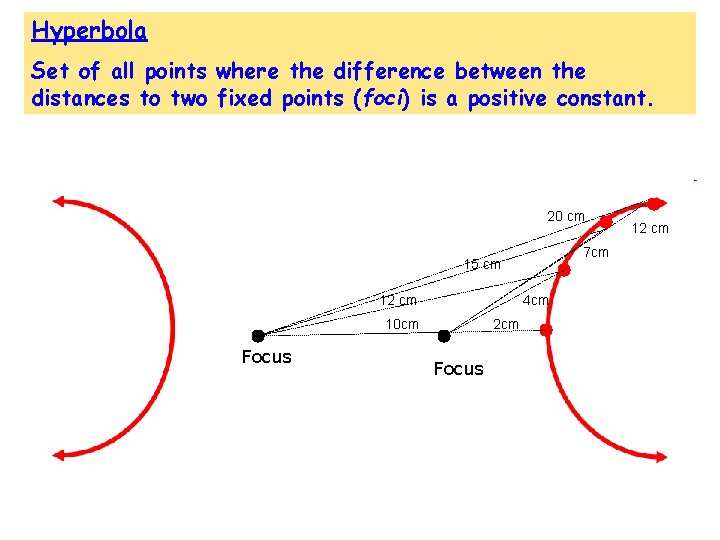
Hyperbola Set of all points where the difference between the distances to two fixed points (foci) is a positive constant. 20 cm 7 cm 15 cm 12 cm 4 cm 10 cm Focus 2 cm Focus 12 cm

Other parts of a hyperbola: Axis (transverse) Center Vertices Foci Transversal axis can run vertically

Equation of a Hyperbola Similar to ellipse Horizontal axis Vertical axis Similarities/Differences: • Subtraction between x 2 and y 2 terms • Variable above a determines the direction of axis • a is still the distance from center to a vertex • c is still the distance from center to a focus • c is now larger so…

Example Find the standard form of the equation with foci (-1, 2) and (5, 2) and vertices (0, 2) and (4, 2).

Question: What is b in an hyperbola? It is still a distance from the center in the opposite direction of the axis How it applies to a parabola has to do with a new part unique to hyperbolas. Asymptotes Lines that bound the hyperbola Pass through the diagonals of a rectangle with dimensions 2 a and 2 b

Asymptotes Conjugate axis (h, k + b) (h - a, k) (h + a, k) (h, k - b) b is the distance from center to edge of rectangle along conjugate axis

Equations for Asymptotes Horizontal hyperbola (transverse axis) b is up/down – a is left/right slope is rise over run → Vertical hyperbola (transverse axis) a is up/down – b is left/right slope is rise over run →

Example Sketch the graph of 4 x 2 – y 2 = 16, include the asymptotes.

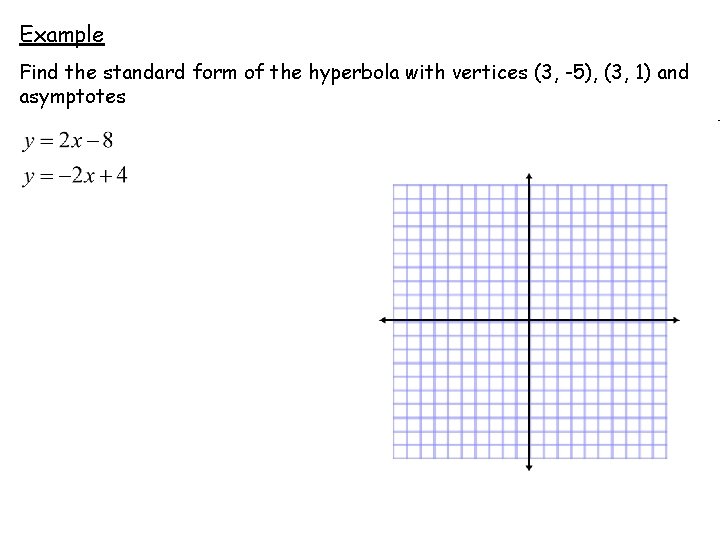
Example Find the standard form of the hyperbola with vertices (3, -5), (3, 1) and asymptotes

Eccentricity of an Hyperbola where e > 1 (since c is larger than a) large e → flatter curve e close to 1 → more curved - pointed Problem Set 9. 3