Lesson 9 3 Angles of Elevation Depression Horizontal

Lesson 9 -3: Angles of Elevation & Depression Horizontal Angle of depression Height Angle of elevation Horizontal

Using Angle of Elevation & Depression Trigonometry can be used to find lengths without actually having to measure. ? ANGLE OF Elevation _______! 400 7920 ft. A map tells this hiker the horizontal _______ distance to a mountain is 1. 5 miles (or 7920 ft. ). An instrument tells him the angle to look up to see 40 degrees the peak of the mountain is ______. Can the hiker tell the height _____ of the mountain?

Using trigonometry, the hiker can find the height: opposite adjacent angle ? = ______; 7920 = ______; ____ is 400; which trig ratio should he use? tangent ____ x 40 ___ x = 6646 ft. 7920 _____ Similar problem: could a person standing on the mountain looking at the hiker find how high they are? 7920 ft. 400 ? ANGLE OF Depression ______! The looks of the triangle may have change but the ________ and _________ have not! Numbers Relationships

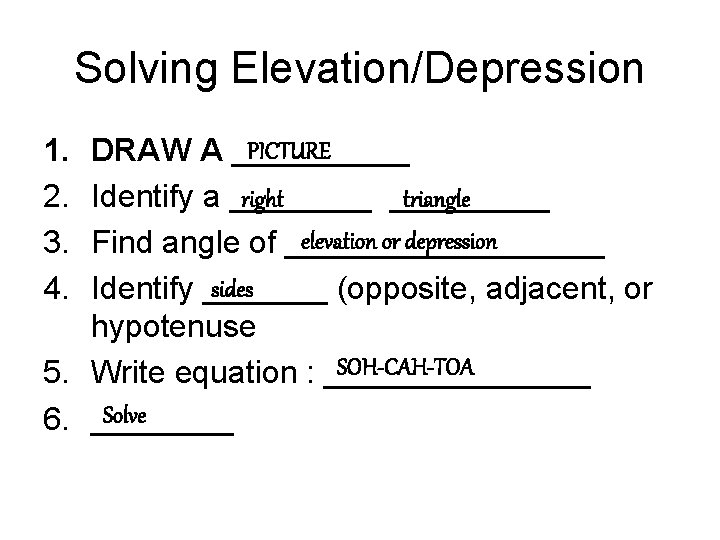
Solving Elevation/Depression 1. 2. 3. 4. PICTURE DRAW A _____ right triangle Identify a _________ elevation or depression Find angle of _________ sides Identify _______ (opposite, adjacent, or hypotenuse SOH-CAH-TOA 5. Write equation : ________ Solve 6. ____

Example 1 A roller coaster car is at one of its highest points. It drops at a angle for 320 feet. How high was the roller coaster car to the nearest foot before it began its fall? Answer: The roller coaster car was about 285 feet above the ground.

Example 2 At the circus, a person in the audience watches the high-wire routine. A 5 -foot-6 -inch tall acrobat is standing on a platform that is 25 feet off the ground. How far is the audience member from the base of the platform, if the angle of elevation from the audience member’s line of sight to the top of the acrobat is Make a drawing Label Identify Equation Solve

Answer: The audience member is about 60 feet from the base of the platform.