Lesson 9 1 Parabolas Write any parts of

Lesson 9. 1 Parabolas Write any parts of a parabola that you know:

Conic Sections Many shapes and curves can be classified as a conic section These shapes can be written algebraically as Ax 2 + Bxy + Cy 2 + Dx + Ey + F = 0 or in relation to a locus (collection) of points (x – h)2 + (y – k)2 = r 2

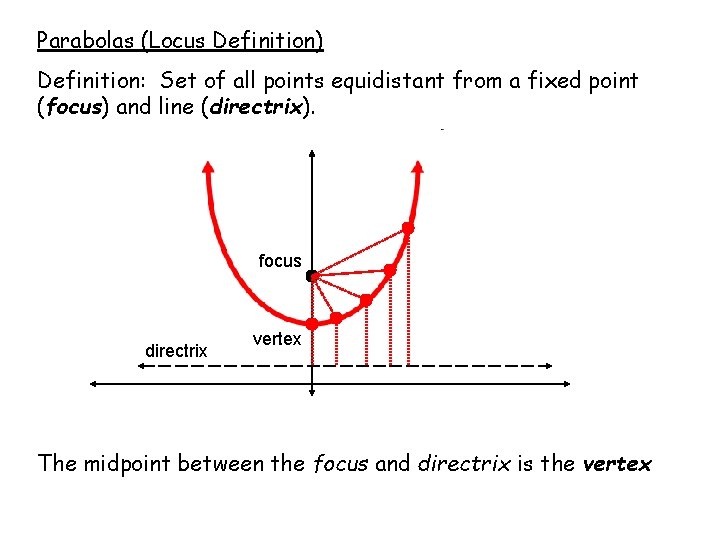
Parabolas (Locus Definition) Definition: Set of all points equidistant from a fixed point (focus) and line (directrix). focus directrix vertex The midpoint between the focus and directrix is the vertex

Standard Equation of a Parabola (Locus) Traditional → Visual → I like → Here, p is the distance from the focus to the vertex p=¼ → Same width as y = x 2 p = larger → Wider than y = x 2 p = smaller → Narrower than y = x 2

Or, we can look at the 4 p 4●p is the focal length: the width of the curve through the focus

Some things to know: 1) A parabola can go Up/Down or Left/Right x-quantity squared → Up/Down y-quantity squared → Left/Right 2) Why do “I like” the last equation? You can see the effects of p or 4 p on the “slope” – a Large p → large 4 p → small a → low slope or flatter parabola Small p → small 4 p → large a → high slope or steeper parabola

Example Find a standard form equation of a parabola with a vertex at the origin and focus at (0, 8)

Example Find the vertex, focus, and equation of the directrix of the parabola. Click for more examples

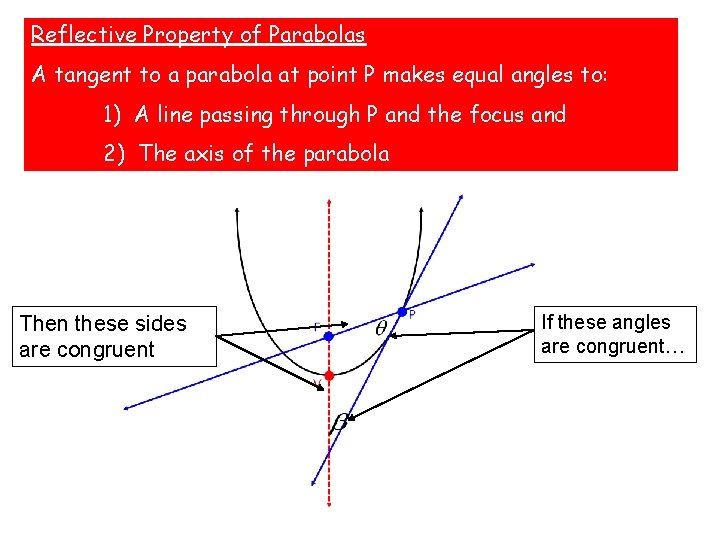
Reflective Property of Parabolas A tangent to a parabola at point P makes equal angles to: 1) A line passing through P and the focus and 2) The axis of the parabola Then these sides are congruent If these angles are congruent…

Example Find the equation of the tangent line to y = x 2 at the point (2, 4).