Lesson 85 Solving problems using the Pythagorean Theorem

Right triangles n The hypotenuse of a right triangle is the side opposite the right angle. (It is also the longest side) n The legs are the sides that form the right angle.

Pythagorean theorem n n If a triangle is a right triangle with legs a and b, and hypotenuse of length c, then a 2 + b 2 = c 2

Calculating missing side lengths n Use Pythagorean theorem to find the missing side lengths c 6 8

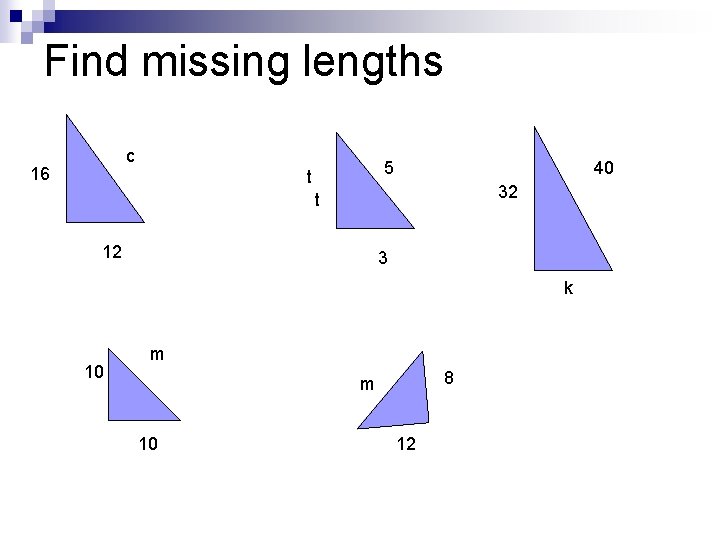
Find missing lengths c 16 5 t 40 32 t 12 3 k 10 m 8 m 10 12

Converse of Pythagorean theorem n If a triangle has side lengths a, b, and c that satisfy the equation a 2 + b 2 = c 2, then the triangle is a right triangle

Pythagorean triples n. A Pythagorean triple is a group of 3 nonzero whole numbers a, b, and c that represent the lengths of the sides of a right triangle. n The most common are the 3, 4, 5 n 5, 12, 13 n Anything that is a multiple of these is also a triple.

Determining a right triangle Determine whether the given side lengths form a Pythagorean triple. n 9, 40, 41 n 8, 10, 12 n 4, 5, 6 n 9, 12, 15 n

Lesson 76 n. Calculating the midpoint and length of a segment

Calculating distance using the Pythagorean theorem n To find the direct distance between the bench and the water fountain, use Pythagorean theorem

Using Pythagorean theorem to find the distance between 2 points Graph the points n Find the horizontal distance and vertical distance by making a right triangle n Use Pythagorean theorem to find the hypotenuse n Find the distance between P(1, 4) and Q(5, 1) n

Distance formula n The distance between 2 points ( x 1, y 1) and (x 2, y 2) is

Finding the distance between 2 points n Use the distance formula to find the distance between (3, -2) and (6, 4)

practice n. Find the distance between ( 2, -2) and (4, -3)

Classifying polygons n n n Determine whether quadrilateral ABCD is a rhombus A(-1, 0) B(2, 1) C(1, -2) D(-2, -3) Graph points Use distance formula to find lengths of each side - AB, BC, CD, AD If all lengths are the same it is a rhombus Is it a rhombus?

Is ABCD a rhombus? A(-1, -4) n B(1, -4) n C(3, -2) n D(1, -2) n

The midpoint formula The midpoint of a line segment is the point that divides the segment into 2 equal-length segments. n The midpoint M of the line segment with endpoints ( x 1, y 1) and (x 2, y 2) is n

Finding the midpoint of a segment Find the midpoint of the line segment with the given endpoints. n (3, 5) and (7, -2) n

practice n Find the midpoint of the line segment with the given endpoints: (7, 10) and ( 5, -4)